点估计
点估计是用样本统计量来估计总体参数,因为样本统计量为数轴上某一点值,估计的结果也以一个点的数值表示,所以称为点估计。点估计和区间估计属于总体参数估计问题。何为总体参数统计,当在研究中从样本获得一组数据后,如何通过这组信息,对总体特征进行估计,也就是如何从局部结果推论总体的情况,称为总体参数估计。
矩估计
矩估计,即矩估计法,也称“矩法估计”,就是利用样本矩来估计总体中相应的参数。首先推导涉及感兴趣的参数的总体矩(即所考虑的随机变量的幂的期望值)的方程。然后取出一个样本并从这个样本估计总体矩。接着使用样本矩取代(未知的)总体矩,解出感兴趣的参数。从而得到那些参数的估计。
区间估计
区间估计是在点估计的基础上,给出总体参数估计的一个区间范围,该区间通常由样本统计量加减估计误差得到。与点估计不同,进行区间估计时,根据样本统计量的抽样分布可以对样本统计量与总体参数的接近程度给出一个概率度量。下面将以总体均值的区间估计为例来说明区间估计的基本原理。
样本量的确定
一、估计总体均值时样本容量的确定
1.重复抽样
一旦确定了置信水平(1-α),Zα/2的值就确定了,对于给定的的值和总体标准差σ,就可以确定任一希望的允许误差所需要的样本容量。令E代表所希望达到的允许误差,即: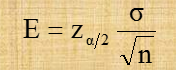
由此可以推到出确定样本容量的公式如下: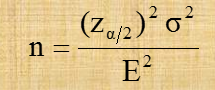
2.不重复抽样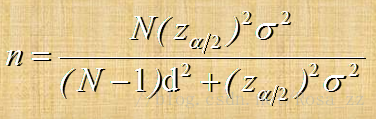
- 样本容量n与总体方差成正比;
- 与绝对误差成反比;
- 与概率度成正比。
二、估计总体比例时样本容量的确定
1.重复抽样
一旦确定了置信水平(1-α),Zα/2的值就确定了。由于总体比例的值是固定的,所以允许误差由样本容量来确定,样本容量越大允许误差就越小。估计的精度就越好。因此,对于给定的的π值,就可以确定任一希望的允许误差所需要的样本容量。令E代表所希望达到的允许误差,即: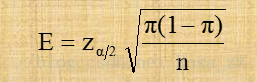
由此可以推导出重复抽样和无限总体抽样条件确定样本容量的公式如下: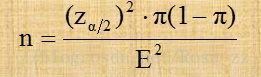
2.不重复抽样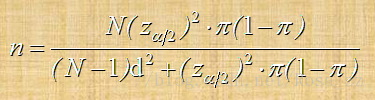
- d的取值一般小于0.1
- π未知,以样本比例p替代
- π或p都未知时,可取0.5,这是一种谨慎估计
影响样本容量n的因素
- 总体个单位之间的差异
- 概率保证程度
- 允许误差的大小
- 抽样方式
- 抽样的组织形式
确定样本容量的注意事项
一、在实际中采用不重复抽样,但常用重复抽样下的公式代替;
二、若和p未知,其处理方式是:
-
用过去近期的数据代替,
-
用样本数据代替,
-
取p=0.5或最接近0.5的值;
三、对同一总体,若求出的Nx,Np不等,这时取较大的作为必要样本容量,
- 以同时满足做两种调查的需要;
四、在实际工作中,常使用重复抽样下的简单随机抽样公式。
来源:CSDN
作者:维生素_M
链接:https://blog.csdn.net/Radio_M/article/details/103656510