秒懂机器学习---机器学习无法逃避的梯度下降法
一、总结
一句话总结:
梯度下降法有其缺陷,但是可以和其它算法配合使用,比如模拟退火等。
1、导数的几何意义是什么?
斜率:导数又叫微分,是图像的斜率。
2、复合函数(比如z=f[u(x,y),v(x,y)])的偏导数的链式求导法则是怎样的?
δz/δx=(δz/δu)*(δu/δx)+(δz/δv)*(δv/δx)
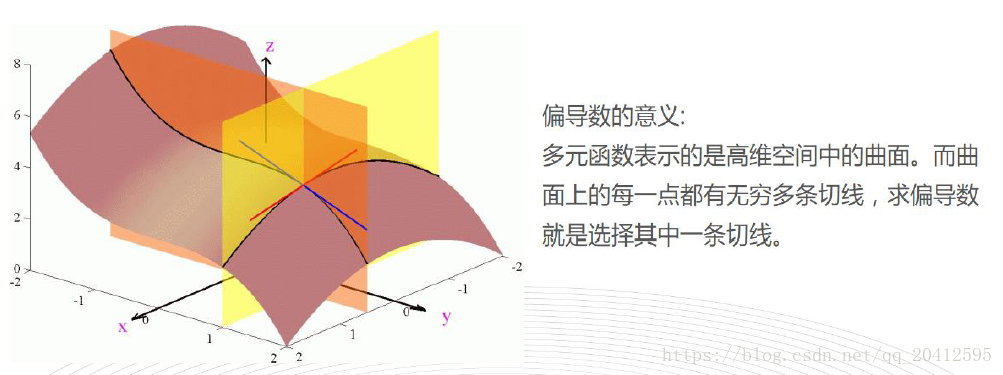
3、偏导数的几何意义是什么?
曲面无数条切线中的一条:多远看书表示的是高维空间中的曲面。而曲面上的每一点都有无穷多条切线,而求偏导数就是选择其中的一条切线。
4、梯度的定义是什么?
某一函数在该点处的方向导数沿着该方向取得最大值:(梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模))
单变量中表示导数或斜率:在单变量的实值函数的情况,梯度只是导数,或者,对于一个线性函数,也就是线的斜率。
5、梯度是向量还是标量?
向量
6、多元函数中的梯度分别为什么?
偏导数:一个n元函数f关于n个变量的偏导数
三元函数f的梯度为(fx,fy,fz),二元函数f的梯度为(fx,fy),一元函数f的梯度为fx
要明确梯度是一个向量,是一个n元函数f关于n个变量的偏导数,比如三元函数f的梯度为(fx,fy,fz),二元函数f的梯度为(fx,fy),一元函数f的梯度为fx。然后要明白梯度的方向是函数f增长最快的方向,梯度的反方向是f降低最快的方向。
7、梯度下降的场景假设?
浓雾环境找山谷:一个人被困在山上,需要从山上下来(i.e. 找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。
从陡峭处往非陡峭处走:以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
二、机器学习之梯度与梯度下降法
转自或参考:机器学习之梯度与梯度下降法
https://blog.csdn.net/qq_20412595/article/details/81409744
1.导数
- 导数的几何意义:导数又叫微分,是图像的斜率。
- 多元函数的偏导数

- 偏导数的几何意义
2.梯度
- 梯度的定义
来自百度:(梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模))
在单变量的实值函数的情况,梯度只是导数,或者,对于一个线性函数,也就是线的斜率。
(注意:梯度是一个向量)
要明确梯度是一个向量,是一个n元函数f关于n个变量的偏导数,比如三元函数f的梯度为(fx,fy,fz),二元函数f的梯度为(fx,fy),一元函数f的梯度为fx。然后要明白梯度的方向是函数f增长最快的方向,梯度的反方向是f降低最快的方向。
3.梯度下降法
-
梯度下降的场景假设
引用《作者:六尺帐篷》
梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景:一个人被困在山上,需要从山上下来(i.e. 找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
梯度下降的基本过程就和下山的场景很类似。
首先,我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值,也就是山底。根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快!因为梯度的方向就是函数之变化最快的方向(在后面会详细解释),所以,我们重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向,也就是场景中测量方向的手段。
-
梯度下降算法的数学解释

此公式的意义是:J是关于Θ的一个函数,我们当前所处的位置为Θ0点,要从这个点走到J的最小值点,也就是山底。首先我们先确定前进的方向,也就是梯度的反向,然后走一段距离的步长,也就是α,走完这个段步长,就到达了Θ1这个点!
- α是什么含义?
α在梯度下降算法中被称作为学习率或者步长,意味着我们可以通过α来控制每一步走的距离,不要走太快,步长太大会错过了最低点。同时也要保证不要走的太慢,太小的话半天都无法收敛。所以α的选择在梯度下降法中往往是很重要的!α不能太大也不能太小,太小的话,可能导致迟迟走不到最低点,太大的话,会导致错过最低点!

- 为什么要梯度要乘以一个负号?
梯度前加一个负号,就意味着朝着梯度相反的方向前进!我们在前文提到,梯度的方向实际就是函数在此点上升最快的方向!而我们需要朝着下降最快的方向走,自然就是负的梯度的方向,所以此处需要加上负号。
4.梯度下降存在的问题
1)梯度下降的问题之一:参数调整缓慢
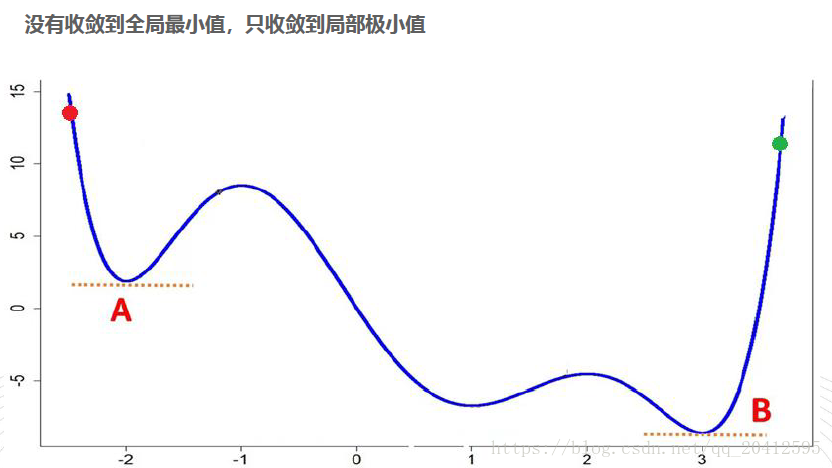
2)梯度下降的问题之二:收敛于局部极小值
来源:https://www.cnblogs.com/Renyi-Fan/p/10977440.html