全排列是面试笔试过程中经常遇到的一个问题。对于练习过的同学来说,这个问题其实
不算一个难题,但是对于没有练习过的同学,或者说只是知道大致思路的同学来说,
要在短时间内写出正确的全排列代码还是有点难度的。
本文是作者在学习全排列时的一个总结笔记,主要包括:
[1]. 全排列的递归实现
[2]. 全排列的非递归实现
[3]. STL中的next_permutation
全排列的递归实现
递归方法的全排列思想挺简单的,就是从第一个数字起,将它与其后面的每个数字
进行交换。
这是大部分教程或博客告诉我们的。我在读完这句话后也觉得挺简单的,就是一个
不断交换的过程嘛,例如“123”的全排列就是将1与后面的每个数字交换得到“213”,
“321”,再将第二个数字与之后的每个数字交换得到“132”,“231”,“312”,这样就
得到了“123”的全排列:123,213,321,132,231,312.
然而,当让我在纸上把代码写出来时,就懵了,不知道要从何入手了。
我对递归的理解也不是很透彻,相信看到这篇文章的你也不会很透彻,
(透彻的话谁还来搜“全排列的递归实现”啊)。
所以,接下来,我们不能用人的思路来考虑问题了,要从计算机的角度出发,从
递归的角度出发来看问题。
那么,问题转化为:输入数据是“123”,期望得到的结果是顺序输出“123”,“132”,
“213”,“231”,“312”,“321”. 程序是一个递归程序,其中涉及到的操作包括
交换每个数字与该数字之后的所有数字。
递归程序需要至少一个变量来控制递归执行的深度,在这里,最外层的递归需要交换
“123”中的第一位与之后的每一位,这样可以获得“123”,“213”,“321”,因为全排列
包括它本身,所以需要与自己交换一次。这之后要控制程序进入第二层递归,也就是
说,要获取第二位之后的所有数字的全排列 …
所以,这里我们用一个变量来控制递归的层次,感觉有点像剥洋葱,一层一层下去,
直到达到洋葱中心(终止条件),再一步一步退出来。
这里,我用idx来表示这个变量,表示当前递归时元素的索引(index)。
至于终止条件,当然是i指向最后一个元素时为止,假如元素有n个,那么i=n就是
递归的终止条件,此时就得到了一组排列,将该组排列输入即可。
由于需要变量i来控制递归的执行,需要元素个数n来获得递归终止条件,当然需要
一个数组或指针来获得所有元素,所以递归程序的函数可以写为:
get_all_permutation(Type* array, int idx, int n)终止条件为:
if (idx==n-1)
print(array);对我来说,写出递归的函数头和终止条件,递归程序就可以说是完成了一半,
很多时候之所以写不出递归程序,就是不明确用哪个变量来控制递归的过程,
什么时候该结束递归。弄明白这两个问题就可以写执行递归的代码了。
for (int i=idx; i<n; ++i) {
// 将第idx个元素依次与后面的元素进行交换
swap(array[idx], array[i]);
// 递归得到idx后面的元素的全排列
get_all_permutation(array, idx+1, n);
}
// 注意:错误代码!!此时,貌似整个代码完成了,让我们以“123”为例,从头执行下该代码:
首先i=idx=0,n=2,array = “123”
交换array[i]与array[idx],array=“123”
对idx+1之后的元素进行全排列,即进入递归的下一层对“23”进行全排列
i=idx=1,交换array[1]与array[1],array=”123”
继续获取idx+1之后的元素的全排列,即进入递归的下一层对“3”进行全排列
此时,满足递归终止条件,打印array,我们顺利获得了“123”.
之后,这次递归终止,一步一步往回退,退到上一层后,所有上一层中
该执行但未执行的都会接着继续执行,也就是说在上面的代码中会进入
下一个for循环,继续接着执行 …
但是,执行该代码你会发现,输出结果是“123”,“132”,“312”,“321”,
“123”,“132”,并不是我们想要的全排列!
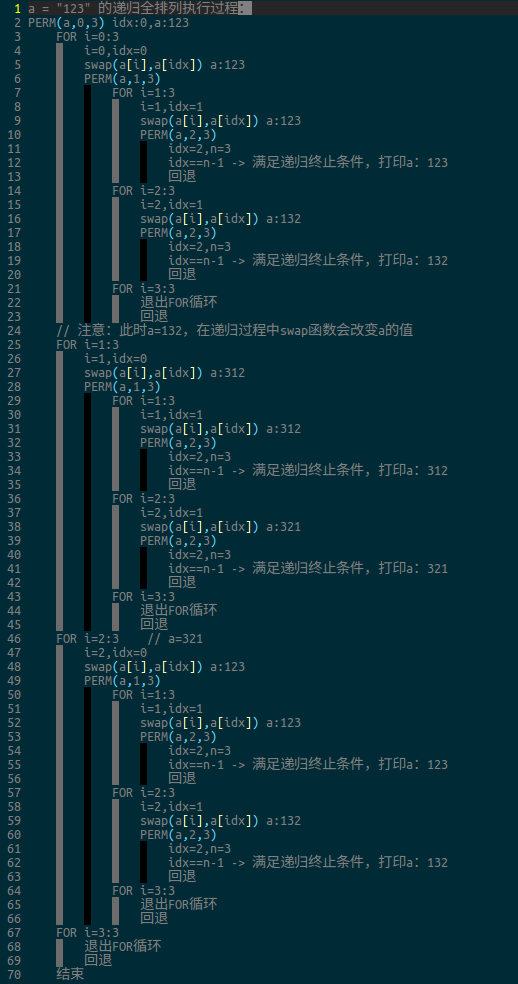
问题出在哪里呢?让我们跟着代码走一遍。
上图是对递归执行过程的一个记录,建议读者自己在纸上对递归程序的执行过程
进行一个手动的推演,这样有利于加深对递归的理解。
其中,要特别注意各个变量的值在递归/回退时是否会改变。
这一点在对字符数组和string类型进行操作时略有差别。
从中可看出,在每次递归中,数组a中的元素所处位置都在变化,这样,回退
到上一层执行“从第一个数字起,将它与其后面的每个数字进行交换”这一步
就得不到满足了,因此在每次循环中执行递归返回后,我们需要再次交换元素
的位置,用以使数组a恢复原样。
这样,修复后的递归代码为:
for (int i=idx; i<n; ++i) {
// 将第idx个元素依次与后面的元素进行交换
swap(array[idx], array[i]);
// 递归得到idx后面的元素的全排列
get_all_permutation(array, idx+1, n);
// 在递归结束回退时恢复数组,确保下一次循环的正确执行
swap(array[idx], array[i]);
}
// 正确代码!!至此,我们已经写出了全排列的递归实现的所有代码了,整理如下:
//全排列的递归实现1
#include <iostream>
using namespace std;
void get_permutation(char *a, int idx, int length)
{
if (idx == length-1){
for (int i=0; i<length; ++i)
cout << a[i];
cout << endl;
}
else {
for (int i=idx; i<length; ++i){
swap(a[i],a[idx]);
get_permutation(a,idx+1,length);
swap(a[i],a[idx]);
}
}
}
int main()
{
char array[] = "123";
get_permutation(array,0,3);
return 0;
}//程序输出结果为:
123
132
213
231
321
312可以看出该程序可以正确输出“123”的全排列。但是,细心的读者可能也发现了,
最后两个顺序反了,虽然也算不上什么大问题,但这个小瑕疵真的很膈应人。
//全排列的递归实现2
#include <iostream>
#include <string>
using namespace std;
void get_permutation(string a, int idx, int length)
{
if (idx == length-1){
for (int i=0; i<length; ++i)
cout << a[i];
cout << endl;
}
else {
for (int i=idx; i<length; ++i){
swap(a[i],a[idx]);
get_permutation(a,idx+1,length);
swap(a[i],a[idx]); // 注释
}
}
}
int main()
{
string a = "123";
get_permutation(a,0,3);
return 0;
}//程序输出结果为:
123
132
213
231
321
312当我们用string来存储字符时,程序的运行结果与用字符数组存储字符时一样。
但是,如果我们将其中的第16行注释掉,此时,程序的输出结果为:
//注释掉程序中第16行后的输出结果
123
132
213
231
312
321一下子完美了…
那么,为什么用string来存储数据就可以得到完全不同的结果呢?
这就是C++中string和字符数组在作为函数参数进行传递时的不同之处。
(这里理解不是很透彻,需要结合递归进行更深入的分析…)
当一个string对象作为参数传递给函数时,传递的是引用的一个copy,原来的引用没有改变。
当一个字符数组作为参数传递给函数时,传递的是这个数组的引用,对它进行函数处理,就是
对原数组进行处理。
从另一个角度看,全排列也就是将第i个数字与其余数字的全排列连接起来
伪代码如下:
String permute(String a[])
{
if (a[].length == 1)
return a[];
for (i = 0, i < a[].length(); i++)
append(a[i], permute(a[].remove(i)));
}全排列的非递归实现
全排列的非递归实现思想是:每次找出当前排列的下一个排列。因此,
问题就转换为,给一个排列,如何找出它的下一个排列。
例如:“95382”的下一个排列是“95823”;
“95832”的下一个排列是“98235”;
“98532”是全排列的最后一个,没有下一个全排列。
从右向左找到第一个逆序的数字,例如“95382”的第一个逆序的数字是‘3’;
从右向左找到第一个大于该逆序数字的数字,“95382”中从右向左大于‘3’
的第一个数字是‘8’;
交换这两个数字的位置,得到“95832”;
再将第一个逆序数字所在位置之后的数字翻转,即得到该排列的下一个排列,
即“95823”.
这样,给定一个排列就可以得到其下一个排列,我们就可以安装这种方法依次打印出
所有排列,就得到了所需的全排列。
代码如下:
#include<iostream>
#include<string>
#include<algorithm>
template<typename Iterator>
bool my_next_permutation(Iterator first, Iterator last)
{
if (first == last) // s="", s.begin()==s.end()
return false;
Iterator i = last;
if (first == --i) // s="1", s.begin()==--s.end()
return false;
//迭代器string.end()指向string最后一个元素的后一个位置
//要获取最后一个元素需要回退一步,即--s.end()指向最后一个元素
//程序运行到此处,i指向最后一个元素,因为i在第二个if语句处
//执行了‘--i’操作
while (true) {
Iterator i1 = i, i2;
if (*--i < *i1) {
i2 = last;
while (!(*i < *--i2))
;
std::iter_swap(i, i2);
std::reverse(i1, last);
return true;
}
if (i == first) {
std::reverse(first, last);
return false;
}
}
}
int main()
{
std::string s = "1232"; //baa
std::sort(s.begin(), s.end());
do{
std::cout << s << '\n';
}while(my_next_permutation(s.begin(), s.end()));
return 0;
}输出结果为:123,132,213,231,312,321
正是我们期望的按顺序的输出。
让我们对该代码中while循环部分进行一个刨根问底的分析。
从头捋一遍,给定一个排列,获得它的下一个排列的方法为:
首先,从右向左找到第一个非递增的数字的位置i,以953882为例,
第一个非递增的数字为3,并记该数字的前一个数字的位置为i1;从最后一个数字开始往左找到第一个大于3(位置i)的数字8,
记其位置为i2(这里的倒数第2位);交换i与i2位置的数字,得到958832;
将i1到结尾的数字逆序,得到958238,此即为953882的下一个排列958238.
STL中的next_permutation
话说,要成为世界第一,就得向世界第一学习。
STL中提供了计算下一个排列的函数next_permutation,利用该函数我们可以方便
地获得全排列。
代码如下:
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
int main()
{
string s = "1232";
sort(s.begin(), s.end());
do{
cout << s << '\n';
}while(next_permutation(s.begin(), s.end()));
return 0;
}这里的next_permutation的实现思想跟第二部分中全排列的非递归实现的思想一样。
下面给出cppreference.com
提供的一种next_permutation的实现方法:
template<class BidirIt>
bool next_permutation(BidirIt first, BidirIt last)
{
if (first == last) return false;
BidirIt i = last;
if (first == --i) return false;
while (true) {
BidirIt i1, i2;
i1 = i;
if (*--i < *i1) {
i2 = last;
while (!(*i < *--i2))
;
std::iter_swap(i, i2);
std::reverse(i1, last);
return true;
}
if (i == first) {
std::reverse(first, last);
return false;
}
}
}这里的next_permutation的实现方法同第二部分,相信读者也看出来了,
在第二部分全排列的非递归实现中所使用的next_permutation的方法就是
cppreference.com
网站所提供的实现方法。所以,该实现方法的具体分析见第二部分内容,
这里就不再赘述了。
总结
[1].全排列的递归方法思路比较简单,代码实现起来也更容易。
但是,它不能解决有重复数字的全排列问题。
另外需要注意的是,对于不同的数据结构(字符数组和字符串),
在代码实现上会有所不同。[2].全排列的非递归实现方法既可以解决无重复字符的全排列问题,
也可以解决有重复数字的全排列问题。但是,相对于递归实现方法来说,
代码实现稍显复杂,需要对获取下一个全排列的算法思路有透彻的理解。
不过,幸运的是,STL算法库中已经封装了实现好的next_permutation()
算法,在不做要求的情况下,我们可以直接拿来使用。
来源:CSDN
作者:狮子HH
链接:https://blog.csdn.net/yingyujianmo/article/details/52046398