应用统计学-回归分析

拟合度使用r^2和Se来检验。

显著性检验中,对于线性model使用ANOVA,对于单独的回归系数使用t检验。
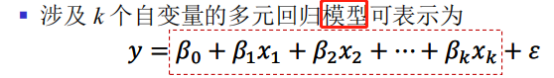

最小二乘法、贝叶斯和最大似然都可用于求回归参数,最小二乘法是最小化残差平方和。
基于model影响变差的因素有随机误差和自变量x。
因为R^2=SST/SSE,所以取值在(0,1)。而Adjusted R^2=MST/MSE,其中SST自由度是n-1,SSR自由度是k,则SSE自由度是n-k-1。
多重相关系数 (multiple correlation coefficient) 又称复相关系数是因变量与所有自变量之间的关系。而相关关系是两两之间的关系。

因为:T(n)=(f(1,n))^1/2所以

多重共线性可能会误导结果,有可能变弱甚至变负。
下面情况暗示存在多重共线性,Model显著但是单独的回归系数却不显著。

容忍度和y无关

变量数目变大,比如加入细节性分类,则误差变小。

可以使用如下方法确定变量种类:

向前是加入就不能删去。
向后是删去就不能加入。
逐步回归是向前向后相结合,一进一出。
最佳子集是k种因素可以组成2^k个子集,考虑所有组合方式,得到最佳的方式。
在确定了变量种类之后,可以使用f检验来查看是否显著,

对个别值的预测需要还原到原始分布,对平均值的预测不需要,所以范围更小。


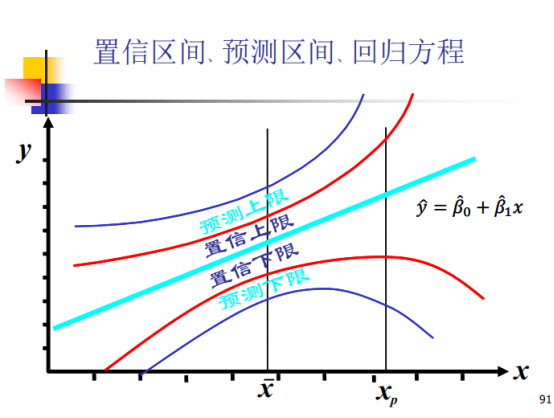
输入数据要在预测范围内,否则造成误导。
残差分析:
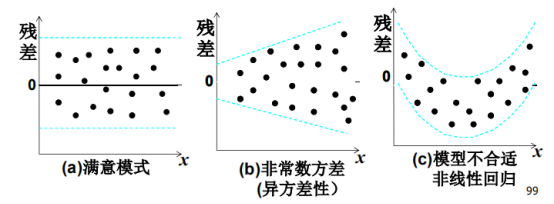
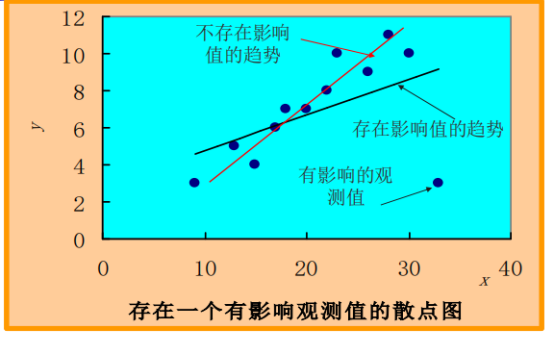
2SD范围内为满意模式,但是不能轻易删除outlier,比如下图就是某点影响了总体趋势。
虚拟变量是将类别变量赋值,加入model,使用regression。