拉普拉斯矩阵是个非常巧妙的东西,它是描述图的一种矩阵,在降维,分类,聚类等的领域有很广泛的应用。
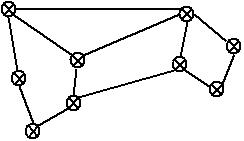
其各个点之间的都有相应的边连接,我们用某个指标(这地方可以任意选择,比如欧氏距离、测地距离、或者高斯相似度等)来衡量两个点的相似度,表示为,没有边连接的其相似度自然为零,是个对称矩阵;某个点的与所有点的相似度之和,表示为;是个对角阵;我们的拉普拉斯矩阵则是

拉普拉斯映射就是直接在低维下找到样本,使得所有样本保持原来的相似度。
求解广义特征向量,取前几个非零最小特值对应的特向,即为原数据在低维下的表示。
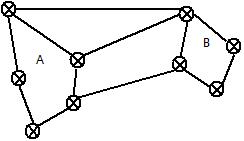
谱图理论需要找个时间看看。
http://student.zjzk.cn/course_ware/web-gcsx/gcsx/chapter5/chapter5_2_1.htm
http://blog.sciencenet.cn/blog-261330-751483.html
http://blog.pluskid.org/?p=287
http://webcache.googleusercontent.com/search?q=cache:_85fSHsIv3MJ:https://zh.wikipedia.org/zh-cn/%25E7%2589%25B9%25E5%25BE%2581%25E5%2590%2591%25E9%2587%258F+&cd=1&hl=zh-CN&ct=clnk&gl=cn&lr=lang_en%7Clang_zh-CN%7Clang_zh-
转自:http://blog.csdn.net/yujianmin1990/article/details/48420483,感谢分享!
来源:博客园
作者:白婷
链接:https://www.cnblogs.com/baiting/p/11531468.html