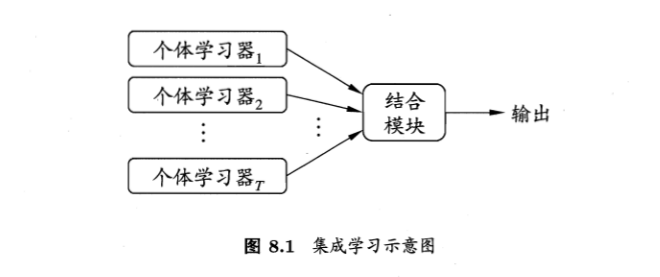
集成学习通过构建并结合多个学习器来完成学习任务,有时也被称为多分类器系统。如下图显示出集成学习的一般结构:先产生一组“个体学习器”,再用某种策略将它们结合起来,个体学习器通常由一个现有的学习算法从训练数据中产生,例如C4.5决策树算法,BP神经网络等。个体学习器可以是相同的类型的学习器也可以是不同类型的,相同类型的称为“基学习器”,不同的称为“组件学习器”或者“个体学习器”。
集成学习通过将多个学习器进行结合,常可获得单一学习器显著优越的泛化性能,这对“弱学习器”(泛化性能略高于随机猜测的学习器)尤为明显,因此集成学习的很多理论都是针对弱学习器进行的。

考虑二分类的问题$y\in\{-1,+1\}$和真实函数$f$,假定基分类器的错误率为$\epsilon$,即对每个基分类器$h_{i}$有
$P(h_{i}\neq f(x))=\epsilon$
假设集成通过简单投票法结合T个基分类器,若有超过半数的基分类器正确,则集成分类就正确:
$H(x)=sign(\sum_{i=1}^{T}h_{i}(x))$
假设基分类器的错误率相对独立,则由$Hoeffding$不等式可知,集成的错误率为:
上式显示出,随着集成中个体分类器数目T的增大,集成的错误率将指数级下降,最终趋于0。
上面的假设是个体分类器中时相对独立的,在现实任务中,个体学习器是为解决同一个问题训练出来的,它们显然不可能独立。事实上,个体学习器的“准确性”和“多样性”本身就存在冲突。
根据个体学习器的生成方式,目前的集成学习方法大致可以分为2大类,即个体学习器间存在强依赖关系,必须串行生成的序列化方法,以及个体学习器间不存在强依赖关系、可同时生成的并行化方法,前者的代表是$Boosting$,后者的代表是$Bagging$和“随机森林”。
Boosting:
是一族可将弱学习器提升为强学习器的算法,这族算法的工作机制类似:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后j基于调整后的样本分布来训练下一个基学习器;如此重复进行,直至基学习器数目达到事先指定的值T,最终将这T个基学习器进行加权结合。
AdaBoost(基学习器的线性组合,二分类问题):
$H(x)=\sum_{t=1}^{T}a_{t}h_{t}(x)$
来最小化指数损失函数:
$\iota_{exp} (H|D)=E_{x\sim D}[e^{-f(x)H(x)}]$

若$H(x)$能令指数损失函数最小化,则考虑损失函数对$H(x)$求偏导($f(x)\in \{-1,+1\}$):
$\frac{\partial \iota_{exp} (H|D)}{\partial H(x)}=-e^{-H(x)}P(f(x)=1|x)+e^{H(x)}P(f(x)=-1|x)$
令上式等于零:
$H(x)=\frac{1}{2}ln\frac{P(f(x)=1|x)}{P(f(x)=-1|x)}$
因此有:
$sign(H(x))=sign(\frac{1}{2}ln\frac{P(f(x)=1|x)}{P(f(x)=-1|x)})$
$=\left\{\begin{matrix}1,P(f(x)=1|x) > P(f(x)=-1|x)\\ -1,P(f(x)=1|x) < P(f(x)=-1|x)\end{matrix}\right.$
$=\underset{y \in \{-1,+1\}}{arg\ max}\ P(f(x)=y|x)$
这意味着$sign(H(x))$达到了贝叶斯最优的错误率,即指数损失函数和0/1损失函数是等价的。指数损失函数可以代替0/1损失函数,它具有更好的数学性质(连续可微的)
在AdaBoost算法中,第一个基分类器$h_{1}$是通过直接将基学习器算法用于初始数据分布而得,此后迭代的生成$h_{t}$和$a_{t}$,当基分类器$h_{t}$基于分布$D_{t}$产生后,该基分类器的权重$a_{t}$应使得$a_{t}h_{t}$最小化指数损失函数:
$\iota_{exp}(a_{t}h_{t}|D_{t})=E_{x\sim D_{t}}[e^{-f(x)a_{t}h_{t}}]$
$=E_{x\sim D_{t}}[e^{-a_{t}}\mathbb{I}(f(x)=h_{t}(x))+e^{a_{t}}\mathbb{I}(f(x)\neq h_{t}(x))]$
$=e^{-a_{t}}(1-\epsilon_{t})+e^{a_{t}}\epsilon_{t}$
考虑指数损失函数的导数:
$\frac{\partial \iota_{exp}(a_{t}h_{t}|D_{t})}{\partial a_{t}}=-e^{-a_{t}}(1-\epsilon_{t})+e^{a_{t}}\epsilon_{t}$
令上式等于零:
$a_{t}=\frac{1}{2}ln(\frac{1-\epsilon_{t}}{\epsilon_{t}})$
这就是Adaboost的权重迭代公式。
Adaboost算法在获得$H_{t-1}$之后样本分布将进行调整,使下一轮的基学习器$h_{t}$能纠正$H_{t-1}$的一些错误,理想的$h_{t}$能纠正$H_{t-1}$的全部错误,即最小化:
$\iota_{exp}(H_{t-1}+h_{t}|D)=E_{x\sim D}[e^{-f(x)(H_{t-1}(x)+h_{t}(x))}]=E_{x\sim D}[e^{-f(x)H_{t-1}(x)}e^{-f(x)h_{t}(x)}]$
注意到$f^{2}(x)=h_{t}^{2}(x)=1$,则$e^{-f(x)h_{t}(x)}$泰勒展开:
$\iota_{exp}(H_{t-1}+h_{t}|D)\simeq E_{x\sim D}[e^{-f(x)H_{t-1}(x)}(1-f(x)h_{t}(x)+\frac{f^{2}(x)h_{t}^{2}(x)}{2})]$
$=E_{x\sim D}[e^{-f(x)H_{t-1}(x)}(1-f(x)h_{t}(x)+\frac{1}{2})]$
于是理想的基学习器是:
$h_{t}(x)=\underset{h}{arg\ min}\ \iota_{exp}(H_{t-1}+h_{t}|D)$
$=\underset{h}{arg\ min}\ E_{x\sim D}[e^{-f(x)H_{t-1}(x)}(1-f(x)h_{t}(x)+\frac{1}{2})]$
$=\underset{h}{arg\ max}\ E_{x\sim D}[e^{-f(x)H_{t-1}(x)}f(x)h_{t}(x)]$(因为$E_{x\sim D}[e^{-f(x)H_{t-1}(x)}]$是一个常数)
$=\underset{h}{arg\ max}\ E_{x\sim D}[\frac{e^{-f(x)H_{t-1}(x)}}{E_{x\sim D}[e^{-f(x)H_{t-1}(x)}]}f(x)h_{t}(x)]$
因为$E_{x\sim D}[e^{-f(x)H_{t-1}(x)}]$是一个常数,令$D_{t}$表示一个分布:
$D_{t}(x)=\frac{D_{t}(x)e^{-f(x)H_{t-1}(x)}}{E_{x\sim D}[e^{-f(x)H_{t-1}(x)}]}$
即:
$D_{t}(x)$是$X$
$\frac{e^{-f(x)H_{t-1}(x)}}{E_{x\sim D}[e^{-f(x)H_{t-1}(x)}]}$是分布概率
则根据数学期望的定义,则等价于令:
$h_{t}(x)=\underset{h}{arg\ max}\ E_{x\sim D}[\frac{e^{-f(x)H_{t-1}(x)}}{E_{x\sim D}[e^{-f(x)H_{t-1}(x)}]}f(x)h(x)]$
$\underset{h}{arg\ max}\ E_{x\sim D_{t}}[f(x)h(x)]$
由于$f(x),h(x)\in \{-1,+1\}$,令:
$f(x)h(x)=1-2\mathbb{I}(f(x)\neq h(x))$
则理想的基学习器:
$\underset{h}{arg\ min}\ E_{x\sim D_{t}}[f(x)\neq h(x)]$
考虑到$D_{t}$和$D_{t+1}$的关系:
$D_{t+1}(x)=\frac{D(x)e^{-f(x)H_{t}(x)}}{E_{x\sim D}[e^{-f(x)H_{t}(x)}]}$
$=\frac{D(x)e^{-f(x)H_{t-1}(x)}e^{-f(x)a_{t}h_{t}(x)}}{E_{x\sim D}[e^{-f(x)H_{t}(x)}]}$
$=D(x)e^{-f(x)a_{t}h_{t}(x)}\frac{E_{x\sim D}[e^{-f(x)H_{t-1}(x)}]}{E_{x\sim D}[e^{-f(x)H_{t}(x)}]}$
这就是样本分布的更新公式
来源:博客园
作者:小xxxx程序员
链接:https://www.cnblogs.com/xcxy-boke/p/11470677.html