对于协方差矩阵的概念,我只想说,该来的总是要来,躲得了今天跑不了明天。所以今天在此想通过这边文章彻底搞清楚这个梗!(纯手工,有什么不妥的地方,望大家的指点与谅解!) 说起协方差矩阵,自然就会想到均值,期望,方差・・・这一系列的统计学概念。(这里提示一下,很多文章都说,均值是统计学的概念,期望是概率论的概念・・・至于两者的历史范畴犹如老树盘根,这里我就不多絮了,大家可以看看相关文章!)接下来就由浅入深的说一下这些概念和相关的公式。 首先说一下均值,均值是一个统计量,是对一次实验的观察与统计。而期望是一种概率论概念,是一个数学特征。比方做一个实验,掷5次骰子,统计一下它们出现的点数,5次骰子出现的点数分别为2 4 5 1 6,那我们可以说这次实验的样本均值是(2+4+5+1+6)/5 = 3.6,但是期望不能说是3.6,因为我们仅仅掷了5次骰子。当随着次数的不断增多,我们会发现样本均值会无限趋近一个数 3.5!而这个3.5就是期望。由此可以看出,均值跟期望的关系 犹如频率和概率的关系!也可以说他们之间的关系是完全一致的,因为均值就等于随机事件中随机变量与它出现的频率相乘求和,而期望就是随机事件中所有的随机变量与它的概率相乘求和!!因此大多数文章中都会总结到: 概率是频率随样本趋于无穷的极限 期望是平均数随样本趋于无穷的极限 均值的公式为: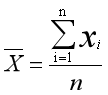
所以均值描述的是一个样本集合的中间点,随机变量的一个特征常数。但是只有均值一个特征往往还不能完全描述随机变量,有时候我们还要了解一个样本集合中所有样本点与这个中间点的差值,差值代表波动,波动代表稳定性!随机变量的稳定性是至关重要的,这就好比偏科的问题!!所以我们引进了方差这个数字特征。由此可以看出,方差表示的是随机变量与均值之间的偏差。而标准差则是方差的开方。
方差公式为: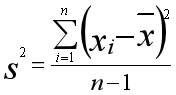
标准差公式为: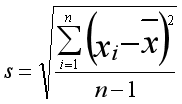
以上的统计量只是用来描述一维数据,当我们遇到多维随机变量的时候,这时候还需要描述一下它们之间的相互关系,相互关系的这种数字特征就是我们所说的协方差,(由此又引出相关系数的概念,)将不同维度之间的协方差组成一个矩阵即为协方差矩阵。(有点乱,再盘一下!嗯~协方差描述的是:样本集合中不同维度的随机变量之间的相互关系,而协方差矩阵是将这些协方差组成一个矩阵!)有点晕菜,给大家举个列子,假设三维随机变量(X Y Z),我们可以求得很多协方差,如cov(X,X),cov(X,Y),cov(X,Z),cov(Y,X),cov(Y,Y),cov(Y,Z),cov(Z,X),cov(Z,Y),cov(Z,Z),协方差矩阵就是将它们写成矩阵的形式。接下来还以三维随机变量(X ,Y ,Z)为例来给出它们的公式
协方差公式为:
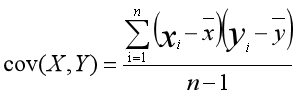
相关系数的公式为: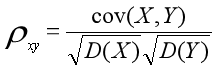
协方差矩阵公式为:
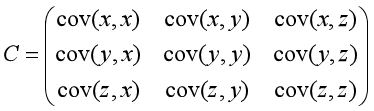
其中cov(x,y)=cov(y,x),而且cov(x,x)就等于随机变量X的方差,所以协方差矩阵是一个对角矩阵,对角线上分别为随机变量X Y Z的方差(在此还要提醒!协方差描述的是样本中不同维数之间的相互关系,多维的随机变量中每一维之间的相互关系!因此当我们求一个行向量或者一个列向量的协方差时,就是在求它的方差。因为它只有一维,只能自己跟自己有关系!!所以向量的协方差矩阵只能是一个数喽!!或者你可以理解为一行一列的矩阵!!哈哈)
为了让大家更好的理解协方差矩阵,我粗糙的写了一个求协方差矩阵的函数(matlab平台),对比一下matlab自带的cov()函数,结果还是令人满意的!


函数的功能就是输入一个矩阵,返回它的协方差矩阵,有点糙!望见解。大家看了文章以后若是还有什么不太理解的,可以结合代码自己实验一下!