所以,这个公式我们写作ax+by = d,(gcd(a, b) | d)
上面的思想是以递归定义的,因为 gcd 不断的递归求解一定会有个时候 b=0,所以递归可以结束。
这样我们就可以给出我们的代码了:
void ex_gcd(int a, int b, int &x, int &y, int &d) { d = a; if (b == 0) { x = 1; y = 0; } else { ex_gcd(b, (a%b), y, x, d); y -= (a/b)*x; } } 上面的代码只是求出了方程 ax+by=gcd(a,b) 的解,但是对于解的形式没有限制
扩展:扩展欧几里得求解 ax + by = c 的最小正整数解(x,y)
当c%gcd != 0 则说明这个方程无解!
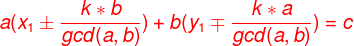
根据这个式子我们不难看出:
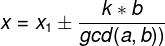
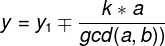
这里以求解最小正整数x为例:
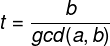
于是我们就可以得到最小正整数的解
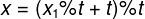
运用ex_gcd的时候,因为a,b,c可能为负值,即我们的t可能会为负数
这个时候我们就要让
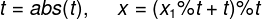
同理如果求最小正整数的解y
就让t = a/gcd(a,b)
y = (y1 % t + t) % t


#include<iostream> using namespace std; long long int exgcd(long long int a,long long int b,long long int &x,long long int &y) { if(b==0) { x=1; y=0; return a; } long long int gcd = exgcd(b,(a%b),y,x); y -= (a/b)*x; return gcd; } int main() { long long int x,y,n,m,l,a,b,c,gcd; while(cin>>x>>y>>m>>n>>l) { a=n-m; b=l; c=x-y; gcd=exgcd(a,b,x,y); if(c%gcd!=0) cout<<"Impossible"<<endl; else { long long int t = b/gcd; x*=(c/gcd); if (t<0) t=-t; x=(x%t+t)%t; cout<<x<<endl; } } return 0; }