傅里叶变换 (FT) 是一个很重要的图像处理工具,用于将图像分解为频率组件。FT 的输出表 示频域内的图像,而输出图像等同于空间域 (x, y)。在频域图像中,每个点表示空间域中包 含的特定频率。因此,对于有很多高频组件(边缘、角落和条纹)的图像,频域中将有很多 点的频率值很高。
以下是傅里叶变换的代码:
import numpy as np import matplotlib.pyplot as plt import cv2 %matplotlib inline #Read in the images image_stripes = cv2.imread('images/stripes.jpg') #Change color to RGB (from BGR) image_stripes = cv2.cvtColor(image_stripes, cv2.COLOR_BGR2RGB) #Read in the images image_solid = cv2.imread('images/pink_solid.jpg') #Change color to RGB (from BGR) image_solid = cv2.cvtColor(image_solid, cv2.COLOR_BGR2RGB) #Display the images f, (ax1,ax2) = plt.subplots(1, 2, figsize=(10,5)) ax1.imshow(image_stripes) ax2.imshow(image_solid)#convert to grayscale to focus on the intensity patterns in the image gray_stripes = cv2.cvtColor(image_stripes, cv2.COLOR_RGB2GRAY) gray_solid = cv2.cvtColor(image_solid, cv2.COLOR_RGB2GRAY) #normalize the image color values from a range of [0,255] to [0,1] for further processing norm_stripes = gray_stripes/255.0 norm_solid = gray_solid/255.0 #perform a fast fourier transform and create a scaled, frequency transform image def ft_image(norm_image): f = np.fft.fft2(norm_image) fshift = np.fft.fftshift(f) ### 将结果转移到屏幕的中央 frequency_tx = 20*np.log(np.abs(fshift)) ## 幅度谱的计算公式 return frequency_tx # Call the function on the normalized images # and display the transforms f_stripes = ft_image(norm_stripes) f_solid = ft_image(norm_solid) # display the images # original images to the left of their frequency transform f, (ax1,ax2,ax3,ax4) = plt.subplots(1, 4, figsize=(20,10)) ax1.set_title('original image') ax1.imshow(image_stripes) ax2.set_title('frequency transform image') ax2.imshow(f_stripes, cmap='gray') ax3.set_title('original image') ax3.imshow(image_solid) ax4.set_title('frequency transform image') ax4.imshow(f_solid, cmap='gray')原图:
效果图: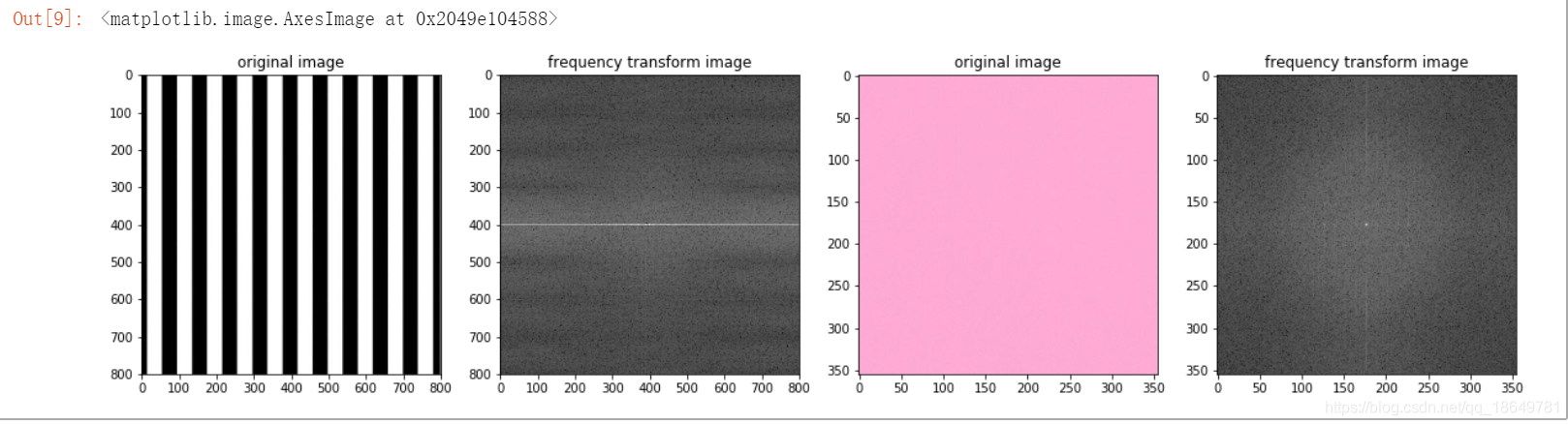
转载请标明出处:OpenCV中的傅里叶变换
文章来源: https://blog.csdn.net/qq_18649781/article/details/88850088