在机器学习中,我们经常要利用极大似然法近似数据整体的分布,本篇文章通过介绍极大似然法及其一些性质,旨在深入浅出地解释清楚极大似然法。
0. 贝叶斯概率
首先看一下经典的贝叶斯公式:
\[
p(Y|X)=\frac{p(X|Y)p(Y)}{p(X)}
\]
其中,\(p(Y)\)称为先验概率(\(prior\)),即根据先验知识得出的关于变量\(Y\)的分布,\(p(X|Y)\)称为似然函数(\(likelihood\)),\(p(X)\)为变量\(X\)的概率,\(p(Y|X)\)称之为条件概率(给定变量\(X\)的情况下\(Y\)的概率,\(posterior\),后验概率)。
1. 似然函数
似然,即可能性;顾名思义,则似然函数就是关于可能性的函数了。在统计学中,它表示了模型参数的似然性,即作为统计模型中参数的函数。一般形式如下:
\[ L(\omega)=p(D | \omega) = p(x_1, x_2, \cdots ,x_n| \omega) \]
其中,\(D\)表示样本集\(\{x_1,x_2,\cdots, x_n\}\), \(\omega\)表示参数向量。
似然函数表示了在不同的参数向量\(\omega\)下,观测数据出现的可能性的大小,它是参数向量\(\omega\)的函数。在某种意义上,我们可以认为其是条件概率的逆反\(^{[1]}\)。
在这里利用Wikipedia\(^{[1]}\)中的例子简要说明一下似然函数,同时也引出极大似然估计。
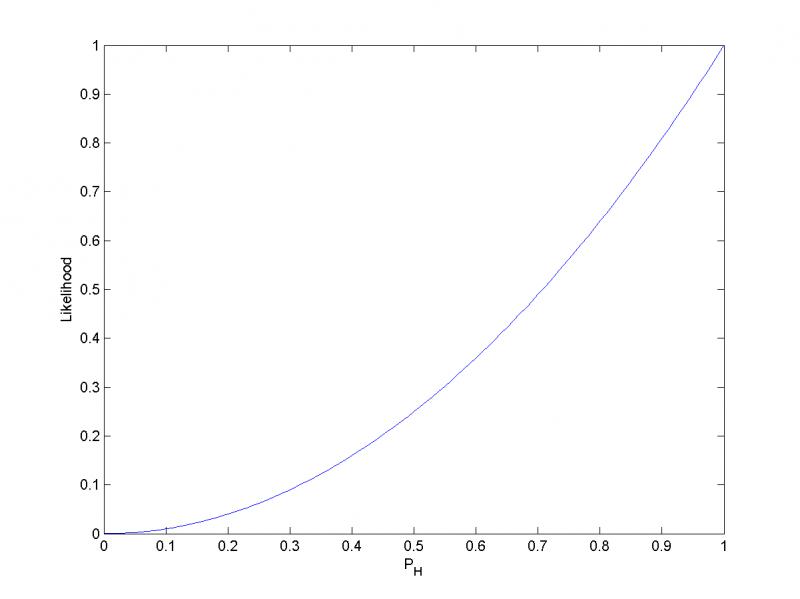
考虑优质一枚硬币的实验,通常来说,我们的硬币都是“公平”(质地均匀)的,即正面向上(Head)的概率\(p_H=0.5\),由此概率我们可以知道投掷若干次后各种结果出现的可能性(概率,或然性)。
例如,投掷硬币两次,两次都为上的概率为0.25,利用条件概率表示,即:
\[ P(HH|p_h=0.5)=0.5^2=0.25 \]
如果一个硬币并非质地均匀,那么它可能是一枚“非公平”的。在统计学中,我们关注的是已知一系列投掷的结果时,关于硬币投掷时正面朝上的可能性的信息。我们可以建立一个统计模型:假设硬币投出时会有\(p_H\)的概率正面朝上,则有\(1-p_H\)的概率反面朝上。这时通过观察已发生的两次投掷,条件概率可以改写成似然函数:
\[ L(p_H)=P(HH|p_H=0.5)=0.25 \]也就是说,对于取定的似然函数,在观测到两次投掷都是正面朝上时,\(p_H\)的似然性是0.25。注意,反之并不成立,即当似然函数为0.25时,不能推论出\(p_H=0.25\)。
如果考虑\(p_H=0.6\),那似然函数也会改变:
\[ L(p_H)=P(HH|p_H=0.6)=0.36 \]
如图所示,注意到似然函数的值变大了。这说明,如果参数\(p_H\)取值变成0.6的话,结果观测到连续两次正面朝上的概率比假设\(p_H=0.5\)时更大,也就是说,参数\(p_H\)取0.6要比取成0.5更有说服力,更为"合理"。
总之,似然函数的重要性不是它的具体取值,而是当参数变化时,函数到底变小还是变大。
对同一个似然函数,其所代表的模型中,某项参数值具有多种可能,但如果存在一个参数值,使得它的函数值最爱的话,那么这个值就是这项参数最为“合理”的参数值。
在这个例子中,\(p_H\)取1时,似然函数达到最大值。也即是,当连续观测到两次正面朝上时,假设硬币投掷时正面朝上的概率为1是最合理的。
在上述引用中,我们看到了一个极端的结论,即未来所有的投掷都会是正面向上,这是频率派观点下使用广泛的一种方法,即极大似然法。在上面的观点中(频率派),\(\omega\)被认为是一个固定的参数,它的值通过估计来确定。但是在贝叶斯派观点中,只有一个数据集\(D\)(即实际观测到的数据集),参数的不确定性通过\(\omega\)的概率分布来表达。贝叶斯的观点是对先验概率的包含是很自然的事情,包含先验概率的贝叶斯方法将不会得到上述的极端结论。
另外还有两点需要注意,第一,似然函数不是\(\omega\)的概率分布,关于\(\omega\)的积分并不一定等于1;第二,似然\(\ne\)概率,概率(或然性)用于在已知一些参数的情况下预测接下来的结果,似然性则是在已知某些结果时,对有关参数进行估值。关于第二点,举个例子,如果我有一枚硬币,如果是质地均匀的(已知参数),那么它出现正面朝上的概率为0.5(结果);同样地,如果一枚硬币,我抛了100次,正面朝上52次(结果),那么我认为硬币十有八九是质地均匀的(估计参数)。
2. 极大似然估计(maximum likelihood estimation, MLE)
了解了似然函数,那么极大似然估计是什么就很好理解了,它是一种用来估计一个概率模型参数的方法。根据公式(2),我们一旦获得一个数据集\(D\),那我们就能求得一个关于\(\omega\)的估计,极大似然估计会寻找一个最可能的值(此处的可能是最可能的\(\omega\),这个\(\omega\)可以使出现采样\(D\)的可能性最大化)。
从数学上来讲,我们可以在\(\omega\)的所有取值中,寻找一个值使得似然函数达到最大值,这种估计方法称之为极大似然估计。极大似然估计是样本不变时,关于\(\omega\)的函数。极大似然估计不一定存在,也不一定唯一。
在第1节中预测硬币的质地\(\omega\),是关于极大似然估计的一个经典例子。其他例子可以查看参考文献\(^{[2]}\)。
现在我们看一下极大似然估计在正态分布中的应用:
现在假定我们有一个观测的数据集\(\mathbf{x}=(x_1,\cdots,x_N)^T\),表示标量变量\(x\)的N次观测。我们假定各次观测是独立地从高斯分布中抽取,分布的均值\(\mu\)和方差\(\sigma^2\)未知,我们想根据数据集来确定这些参数。两个独立事件的联合概率可以由各个事件的边缘概率的乘积得到。我们的数据集\(\mathbf{x}\)是独立同分布的,因此给定\(\mu\)和\(\sigma^2\),我们可以给出高斯分布的似然函数:
\[
p(\mathbf{x}|\mu,\sigma^2)=\prod_{n=1}^{N}\mathcal{N}(x_n|\mu,\sigma^2)
\]
为了简化分析和有助于数值运算,我们取似然函数的对数(最大化对数似然等价于最大化似然函数,很容易证明):
\[
ln(\mathbf x|\mu,\sigma^2)=-\frac {1} {2\sigma^2} \sum_{n=1}^{N}(x_n-\mu)^2-\frac {N}{2}ln\sigma^2-\frac{N}{2}ln(2\pi)
\]
关于\(\mu\),最大化对数似然函数,得到\(\mu\)的最大似然解:
\[
\mu_{ML}=\frac {1}{N} \sum_{n=1}^{N}x_n
\]
可看到解为样本均值。同理,方差\(\sigma^2\)的最大似然解为:
\[
\sigma_{ML}^2=\frac {1}{N} \sum_{n=1}^{N}(x_n-\mu_{ML})^2
\]
由此完成了正态分布的极大似然估计。
3. 极大似然的有偏性
极大似然估计方法求解参数有一定局限性\(^{[3]}\),极大似然法除了会得出第1节中关于硬币的极端情况外,还会出现一种情况,有偏估计,就是期望\(\ne\)理想值。最大似然方法会系统化地低估分布的方差。下面进行证明:
均值的估计\(\mu_{ML}\)的期望\(E[\mu_{ML}]\)为:
\[
E(\mu_{ML})=E(\frac{1}{N} \sum_{n=1}^{N}x_n)=\frac {1}{N}E({\sum_{n=1}^{N}x_n})=\frac{1}{N}\sum_{n=1}^{N}E(x_n)=\mu
\]
方差的估计\(\sigma^2\)的期望\(E[\sigma_{ML}^2]\)为:
\[
E[\sigma_{ML}^2]=E(\frac {1}{N} \sum_{n=1}^{N}(x_n-\mu_{ML})^2)=E(\frac{1}{N}\sum_{n=1}^{N}x_n^2-\mu_{ML}^2)=\frac {1}{N}\sum_{n=1}^{N}E(x_n^2)-E(\mu_{ML}^2)
\]
然后求其后两项,正态分布的二阶矩为
\[
E(x_n^2)=\mu^2+\sigma^2
\]
而
\[ E(\mu_{ML}^2)=E((\frac{x_1+x_2+x_3+\cdots+x_n}{n})^2)=\frac{1}{n^2}(n^2\mu^2+n\sigma^2) \]
故:
\[
E[\sigma_{ML}^2]=\frac{n-1}{n}\sigma^2
\]
由此证明了极大似然的有偏性。其中公式(12)和公式(13)的证明可自行参考正态分布的基础知识。
在这里,PRML\(^{[3]}\)给出了更直观地解释,如下图:
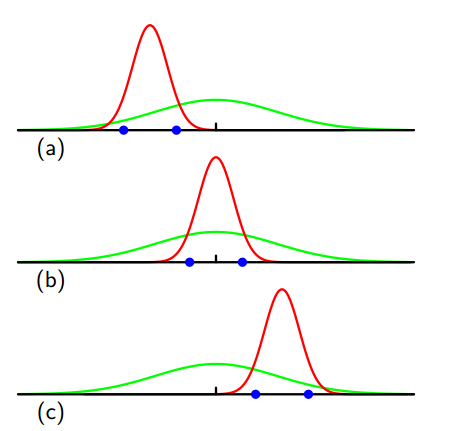
其中,绿色曲线表示真实高斯分布,数据点是根据此概率分布生成,三条红色分别拟合了三个高斯概率分布,每个数据集包含了两个蓝色数据点,对三个数据集求平均,很明显方差被低估了。因为它是相对样本均值进行测量的,而不是相对真实的均值进行测量
4. 后记
极大似然作为机器学习中的一种最常用方法,深刻理解其含义是非常必要且有用的,应该像这对于理解概率论和一些常见的模型有着很大的帮助。当然,极大似然法还有一些性质,如泛函不变性,渐行线行为,限于时间精力和个人水平,没有给出证明,读者可自行参考维基百科\(^{[2]}\)。文章中大部分内容为总结和摘抄,共勉。
参考文献: