条件随机场CRF原理介绍以及Keras实现

本文是对CRF基本原理的一个简明的介绍。当然，“简明”是相对而言中，要想真的弄清楚CRF，免不了要提及一些公式，如果只关心调用的读者，可以直接移到文末。

图示 #

按照之前的思路，我们依旧来对比一下普通的逐帧softmax和CRF的异同。

逐帧softmax #

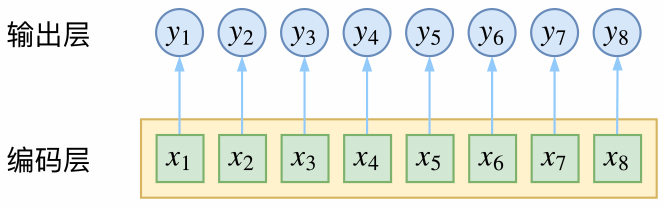
CRF主要用于序列标注问题，可以简单理解为是给序列中的每一帧都进行分类，既然是分类，很自然想到将这个序列用CNN或者RNN进行编码后，接一个全连接层用softmax激活，如下图所示

逐帧softmax并没有直接考虑输出的上下文关联

条件随机场 #

然而，当我们设计标签时，比如用s、b、m、e的4个标签来做字标注法的分词，目标输出序列本身会带有一些上下文关联，比如s后面就不能接m和e，等等。逐标签softmax并没有考虑这种输出层面的上下文关联，所以它意味着把这些关联放到了编码层面，希望模型能自己学到这些内容，但有时候会“强模型所难”。

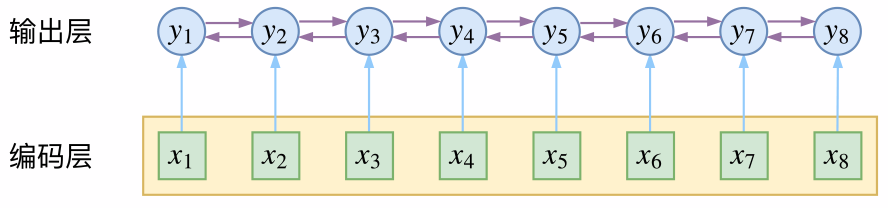
而CRF则更直接一点，它将输出层面的关联分离了出来，这使得模型在学习上更为“从容”：

CRF在输出端显式地考虑了上下文关联

数学 #

当然，如果仅仅是引入输出的关联，还不仅仅是CRF的全部，CRF的真正精巧的地方，是它以路径为单位，考虑的是路径的概率。

模型概要 #

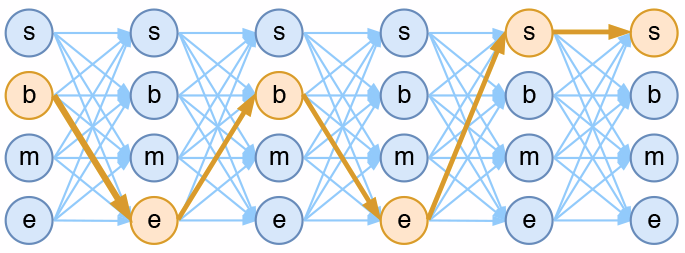
假如一个输入有 $n$ 帧，每一帧的标签有 $k$ 种可能性，那么理论上就有 $k^{n}$ 中不同的输出。我们可以将它用如下的网络图进行简单的可视化。在下图中，每个点代表一个标签的可能性，点之间的连线表示标签之间的关联，而每一种标注结果，都对应着图上的一条完整的路径。

4tag分词模型中输出网络图

而在序列标注任务中，我们的正确答案是一般是唯一的。比如“今天天气不错”，如果对应的分词结果是“今天/天气/不/错”，那么目标输出序列就是bebess，除此之外别的路径都不符合要求。换言之，在序列标注任务中，我们的研究的基本单位应该是路径，我们要做的事情，是从 $k^{n}$ 条路径选出正确的一条，那就意味着，如果将它视为一个分类问题，那么将是 $k^{n}$ 类中选一类的分类问题！

这就是逐帧softmax和CRF的根本不同了：前者将序列标注看成是 $n$ 个 $k$ 分类问题，后者将序列标注看成是 $1$ 个 $k^{n}$ 分类问题。

具体来讲，在CRF的序列标注问题中，我们要计算的是条件概率

P (y 1, \dots, y n | x 1, \dots, x n) = P (y 1, \dots, y n | x), x = (x 1, \dots, x n) (1)

为了得到这个概率的估计，CRF做了两个假设：

假设一 该分布是指数族分布。

这个假设意味着存在函数 $f (y_{1}, \dots, y_{n}; x)$ ，使得

P (y 1, \dots, y n | x) = 1 Z ( x ) exp (f (y 1, \dots, y n; x)) (2)

其中

Z (x)

是归一化因子，因为这个是条件分布，所以归一化因子跟

x

有关。这个

f

函数可以视为一个打分函数，打分函数取指数并归一化后就得到概率分布。

假设二 输出之间的关联仅发生在相邻位置，并且关联是指数加性的。

这个假设意味着 $f (y_{1}, \dots, y_{n}; x)$ 可以更进一步简化为

f (y 1, \dots, y n; x) = h (y 1; x) + g (y 1, y 2; x) + h (y 2; x) + g (y 2, y 3; x) + h (y 3; x) + \dots + g (y n - 1, y n; x) + h (y n; x) (3)

这也就是说，现在我们只需要对每一个标签和每一个相邻标签对分别打分，然后将所有打分结果求和得到总分。

线性链CRF #

尽管已经做了大量简化，但一般来说， $(3)$ 式所表示的概率模型还是过于复杂，难以求解。于是考虑到当前深度学习模型中，RNN或者层叠CNN等模型已经能够比较充分捕捉各个 $y$ 与输入 $x$ 的联系，因此，我们不妨考虑函数 $g$ 跟 $x$ 无关，那么

f (y 1, \dots, y n; x) = h (y 1; x) + + g (y 1, y 2) + h (y 2; x) + \dots g (y n - 1, y n) + h (y n; x) (4)

这时候

g

实际上就是一个有限的、待训练的参数矩阵而已，而单标签的打分函数

h (y_{i}; x)

我们可以通过RNN或者CNN来建模。因此，该模型是可以建立的，其中概率分布变为

P (y 1, \dots, y n | x) = 1 Z ( x ) exp (h (y 1; x) + \sum k = 1 n - 1 [g (y k, y k + 1) + h (y k + 1; x)]) (5)

这就是线性链CRF的概念。

归一化因子 #

为了训练CRF模型，我们用最大似然方法，也就是用

- log P (y 1, \dots, y n | x) (6)

作为损失函数，可以算出它等于

- (h (y 1; x) + \sum k = 1 n - 1 [g (y k, y k + 1) + h (y k + 1; x)]) + log Z (x) (7)

其中第一项是原来概率式的分子的对数，它目标的序列的打分，虽然它看上去挺迂回的，但是并不难计算。真正的难度在于分母的对数

\log Z (x)

这一项。

归一化因子，在物理上也叫配分函数，在这里它需要我们对所有可能的路径的打分进行指数求和，而我们前面已经说到，这样的路径数是指数量级的（ $k^{n}$ ），因此直接来算几乎是不可能的。

事实上，归一化因子难算，几乎是所有概率图模型的公共难题。幸运的是，在CRF模型中，由于我们只考虑了临近标签的联系（马尔可夫假设），因此我们可以递归地算出归一化因子，这使得原来是指数级的计算量降低为线性级别。具体来说，我们将计算到时刻 $t$ 的归一化因子记为 $Z_{t}$ ，并将它分为 $k$ 个部分

Z t = Z (1) t + Z (2) t + \dots + Z (k) t (8)

其中

Z_{t}^{(1)}, \dots, Z_{t}^{(k)}

分别是截止到当前时刻

t

中、以标签

1, \dots, k

为终点的所有路径的得分指数和。那么，我们可以递归地计算

Z (1) t + 1 = Z (2) t + 1 = Z (k) t + 1 = (Z (1) t G 11 + Z (2) t G 21 + \dots + Z (k) t G k 1) H t + 1 (1 | x) (Z (1) t G 12 + Z (2) t G 22 + \dots + Z (k) t G k 2) H t + 1 (2 | x) ⋮ (Z (1) t G 1 k + Z (2) t G 2 k + \dots + Z (k) t G k k) H t + 1 (k | x) (9)

它可以简单写为矩阵形式

Z t + 1 = Z t G \otimes H (y t + 1 | x) (10)

其中

Z_{t} = [Z_{t}^{(1)}, \dots, Z_{t}^{(k)}]

；而

G

是对矩阵

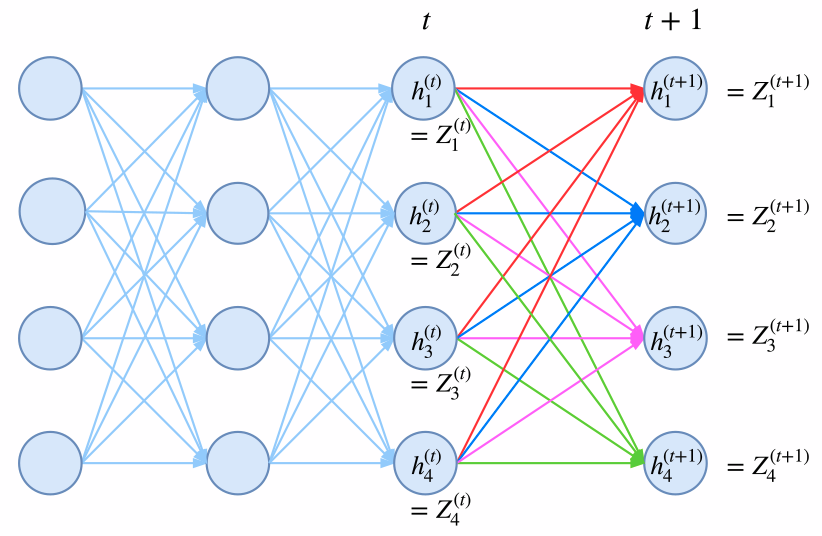
g

各个元素取指数后的矩阵（前面已经说过，最简单的情况下，

g

只是一个矩阵，代表某个标签到另一个标签的分数），即

G_{i j} = e^{g_{i j}}

；而

H (y_{t + 1} | x)

是编码模型

h (y_{t + 1} | x)

（RNN、CNN等）对位置

t + 1

的各个标签的打分的指数，即

H (y_{t + 1} | x) = e^{h (y_{t + 1} | x)}

，也是一个向量。式

(10)

中，

Z_{t} G

这一步是矩阵乘法，得到一个向量，而

\otimes

是两个向量的逐位对应相乘。

归一化因子的递归计算图示。从t到t+1时刻的计算，包括转移概率和j+1节点本身的概率

如果不熟悉的读者，可能一下子比较难接受 $(10)$ 式。读者可以把 $n = 1, n = 2, n = 3$ 时的归一化因子写出来，试着找它们的递归关系，慢慢地就可以理解 $(10)$ 式了。

动态规划 #

写出损失函数 $- \log P (y_{1}, \dots, y_{n} | x)$ 后，就可以完成模型的训练了，因为目前的深度学习框架都已经带有自动求导的功能，只要我们能写出可导的loss，就可以帮我们完成优化过程了。

那么剩下的最后一步，就是模型训练完成后，如何根据输入找出最优路径来。跟前面一样，这也是一个从 $k^{n}$ 条路径中选最优的问题，而同样地，因为马尔可夫假设的存在，它可以转化为一个动态规划问题，用viterbi算法解决，计算量正比于 $n$ 。

动态规划在本博客已经出现了多次了，它的递归思想就是：一条最优路径切成两段，那么每一段都是一条（局部）最优路径。在本博客右端的搜索框键入“动态规划”，就可以得到很多相关介绍了，所以不再重复了～

实现 #

经过调试，基于Keras框架下，笔者得到了一个线性链CRF的简明实现，这也许是最简短的CRF实现了。这里分享最终的实现并介绍实现要点。

实现要点 #

前面我们已经说明了，实现CRF的困难之处是 $- \log P (y_{1}, \dots, y_{n} | x)$ 的计算，而本质困难是归一化因子部分 $Z (x)$ 的计算，得益于马尔科夫假设，我们得到了递归的 $(9)$ 式或 $(10)$ 式，它们应该已经是一般情况下计算 $Z (x)$ 的计算了。

那么怎么在深度学习框架中实现这种递归计算呢？要注意，从计算图的视角看，这是通过递归的方法定义一个图，而且这个图的长度还不固定。这对于pytorch这样的动态图框架应该是不为难的，但是对于tensorflow或者基于tensorflow的Keras就很难操作了（它们是静态图框架）。

不过，并非没有可能，我们可以用封装好的rnn函数来计算！我们知道，rnn本质上就是在递归计算

h t + 1 = f (x t + 1, h t) (11)

新版本的tensorflow和Keras都已经允许我们自定义rnn细胞，这就意味着函数

f

可以自行定义，而后端自动帮我们完成递归计算。于是我们只需要设计一个rnn，使得我们要计算的

Z

对应于rnn的隐藏向量！

这就是CRF实现中最精致的部分了。

至于剩下的，是一些细节性的，包括：

1、为了防止溢出，我们通常要取对数，但由于归一化因子是指数求和，所以实际上是 $\log (\sum_{i = 1}^{k} e^{a_{i}})$ 这样的格式，它的计算技巧是：
$log (\sum i = 1 k e a i) = A + log (\sum i = 1 k e a i - A), A = max {a 1, \dots, a k}$
tensorflow和Keras中都已经封装好了对应的logsumexp函数了，直接调用即可；

2、对于分子（也就是目标序列的得分）的计算技巧，在代码中已经做了注释，主要是通过用“目标序列”点乘“预测序列”来实现取出目标得分；

3、关于变长输入的padding部分如何进行mask？我觉得在这方面Keras做得并不是很好。为了简单实现这种mask，我的做法是引入多一个标签，比如原来是s、b、m、e四个标签做分词，然后引入第五个标签，比如x，将padding部分的标签都设为x，然后可以直接在CRF损失计算时忽略第五个标签的存在，具体实现请看代码。

代码速览 #

纯Keras实现的CRF层，欢迎使用～

# -*- coding:utf-8 -*-

from keras.layers import Layer
import keras.backend as K


class CRF(Layer):
    """纯Keras实现CRF层
    CRF层本质上是一个带训练参数的loss计算层，因此CRF层只用来训练模型，
    而预测则需要另外建立模型。
    """
    def __init__(self, ignore_last_label=False, **kwargs):
        """ignore_last_label：定义要不要忽略最后一个标签，起到mask的效果
        """
        self.ignore_last_label = 1 if ignore_last_label else 0
        super(CRF, self).__init__(**kwargs)
    def build(self, input_shape):
        self.num_labels = input_shape[-1] - self.ignore_last_label
        self.trans = self.add_weight(name='crf_trans',
                                     shape=(self.num_labels, self.num_labels),
                                     initializer='glorot_uniform',
                                     trainable=True)
    def log_norm_step(self, inputs, states):
        """递归计算归一化因子
        要点：1、递归计算；2、用logsumexp避免溢出。
        技巧：通过expand_dims来对齐张量。
        """
        states = K.expand_dims(states[0], 2) # (batch_size, output_dim, 1)
        trans = K.expand_dims(self.trans, 0) # (1, output_dim, output_dim)
        output = K.logsumexp(states+trans, 1) # (batch_size, output_dim)
        return output+inputs, [output+inputs]
    def path_score(self, inputs, labels):
        """计算目标路径的相对概率（还没有归一化）
        要点：逐标签得分，加上转移概率得分。
        技巧：用“预测”点乘“目标”的方法抽取出目标路径的得分。
        """
        point_score = K.sum(K.sum(inputs*labels, 2), 1, keepdims=True) # 逐标签得分
        labels1 = K.expand_dims(labels[:, :-1], 3)
        labels2 = K.expand_dims(labels[:, 1:], 2)
        labels = labels1 * labels2 # 两个错位labels，负责从转移矩阵中抽取目标转移得分
        trans = K.expand_dims(K.expand_dims(self.trans, 0), 0)
        trans_score = K.sum(K.sum(trans*labels, [2,3]), 1, keepdims=True)
        return point_score+trans_score # 两部分得分之和
    def call(self, inputs): # CRF本身不改变输出，它只是一个loss
        return inputs
    def loss(self, y_true, y_pred): # 目标y_pred需要是one hot形式
        mask = 1-y_true[:,1:,-1] if self.ignore_last_label else None
        y_true,y_pred = y_true[:,:,:self.num_labels],y_pred[:,:,:self.num_labels]
        init_states = [y_pred[:,0]] # 初始状态
        log_norm,_,_ = K.rnn(self.log_norm_step, y_pred[:,1:], init_states, mask=mask) # 计算Z向量（对数）
        log_norm = K.logsumexp(log_norm, 1, keepdims=True) # 计算Z（对数）
        path_score = self.path_score(y_pred, y_true) # 计算分子（对数）
        return log_norm - path_score # 即log(分子/分母)
    def accuracy(self, y_true, y_pred): # 训练过程中显示逐帧准确率的函数，排除了mask的影响
        mask = 1-y_true[:,:,-1] if self.ignore_last_label else None
        y_true,y_pred = y_true[:,:,:self.num_labels],y_pred[:,:,:self.num_labels]
        isequal = K.equal(K.argmax(y_true, 2), K.argmax(y_pred, 2))
        isequal = K.cast(isequal, 'float32')
        if mask == None:
            return K.mean(isequal)
        else:
            return K.sum(isequal*mask) / K.sum(mask)

除去注释和accuracy的代码，真正的CRF的代码量也就30行左右，可以说跟哪个框架比较都称得上是简明的CRF实现了吧～

用纯Keras实现一些复杂的模型，是一件颇有意思的事情。目前仅在tensorflow后端测试通过，理论上兼容theano、cntk后端，但可能要自行微调。