预积分皮肤渲染Lut生成实践学习整理

参考：https://zhuanlan.zhihu.com/p/72161323

https://zhuanlan.zhihu.com/p/56052015

https://www.slideshare.net/leegoonz/penner-preintegrated-skin-rendering-siggraph-2011-advances-in-realtime-rendering-course

https://developer.nvidia.com/gpugems/GPUGems3/gpugems3_ch14.html

https://www.w3cschool.cn/ngyasc/q9gm7ozt.html

http://filmicworlds.com/blog/filmic-tonemapping-operators/

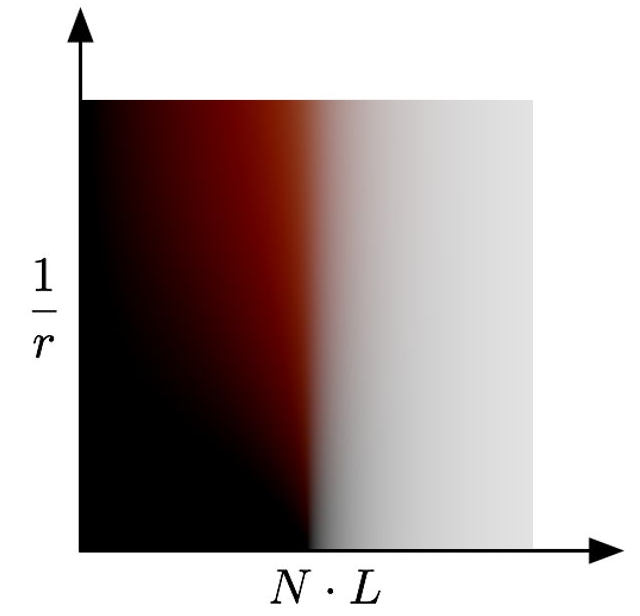
主要讲上面这张图是怎么生成的。

在Pre-integrated Skin Shading（这篇文章收录在《GPU Pro2》和《GPU Gem3》中，还有一个PPT里面说了这张图的来源。

次表面散射

一些说法是，从光源发出的光进入物体内部，经过多次反射、折射、散射及吸收后返回物体表面的光，指的是Diffuse reflection，但在《Real Time Rendering》中把Diffuse Reflection称为Local Subsurface Scattering。

次表面散射，大家都知道是光进入物体内部一通操作后又飞出来，local SSS指的是飞出去的点与最初进入的点之间的距离非常小，可以忽略不计，当作原地飞出。

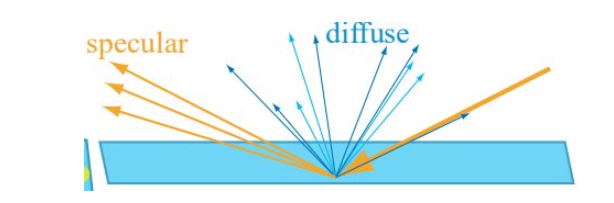
有了local就有Global，Global SSS指的是两点之间的距离无法忽略，比着色的最小单位要大（最小单位可以认为是光栅化后的一个像素）。

如上图，小圈内的是local SSS，大圈内的是Global SSS。

积分

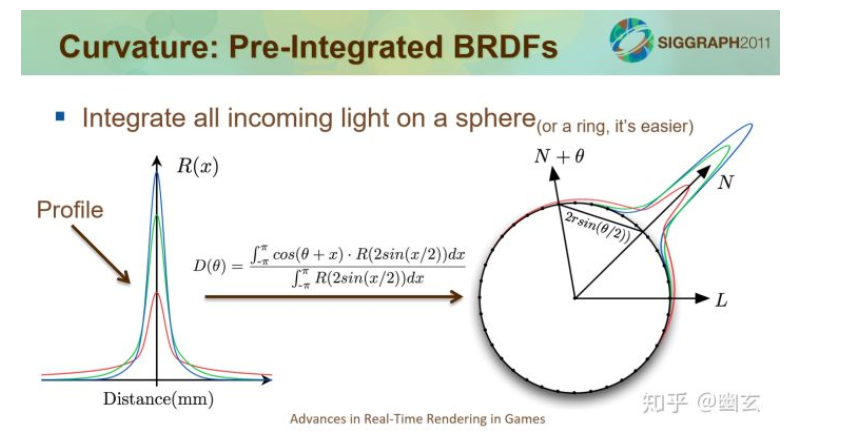
这张图来自这个ppt：https://www.slideshare.net/leegoonz/penner-preintegrated-skin-rendering-siggraph-2011-advances-in-realtime-rendering-course

图上这个方程是

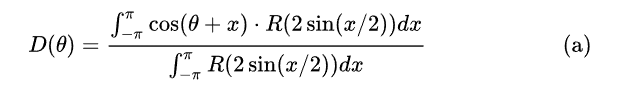
gpu pro2的方程是

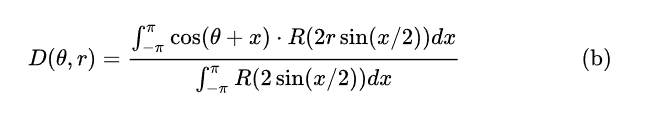
可以看出（2）比（1）多一个r，那么哪个是正确的呢？方程a可能是方程b的r取1时的结果，那么a就先不算错了。

正确方程是

下面来推导，

假设p是屏幕上一点，由于皮肤具有次表面散射的特性，P受到P周围一定范围内的其他点的散射影响，假设是半圆APB的影响。（参考文档2中，认为法线反方向的半球相当于皮肤背面，是不受光照的）。

假设L方向光的辐射度总和位1，取半圆上任意一点Q，则Q点的直接光照亮度为：

法线与OQ之间的夹角为x，法线与L方向的夹角为theta。假设Q点对P点的散射率为q（x），则Q点散射到P点后的亮度为：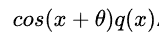

半球上有无限个这样的Q点，我们把这些Q点对P点的贡献做个积分就是P点最后的亮度：

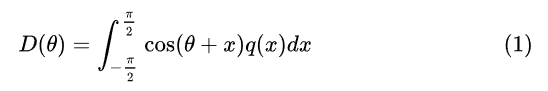
上式（1）中，只有Q点对P点的散射率q（x）是未知的，我们来求q（x）。

根据次表面散射的特征（后面会讲，扩散剖面是与距离有关的），离发射光的点越远的点，受到发射光的点的散射的影响应该越小，所以Q点对P点的散射率应该是一个与距离有关的函数。设d是QP的弦长，则

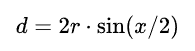
散射是对称的（后面会讲，扩散剖面计算是用的高斯函数，是对称的），也可能是散射是跟距离有关的，所以，Q对P的散射率和P对Q的散射率相等。假设P点受到半圆上其他各点的影响，P点也会影响他周围的半圆上的点。

根据能量守恒定律，P点在整个半圆上的散射率总和应该等于1，所以，实际是一个概率密度函数，满足：

我们的目的是找到q（x），他既满足次表面特征函数（下面会讲，扩散曲面的函数R（d），https://developer.nvidia.com/gpugems/GPUGems3/gpugems3_ch14.html 可参考这篇文章），也要满足能量守恒公式（2）.

但我们不能之间让q（x）=R(d)，因为可能不满足公式（2），即积分不为1。

我们可以令q（x）=kR（d），带入（2），得到：

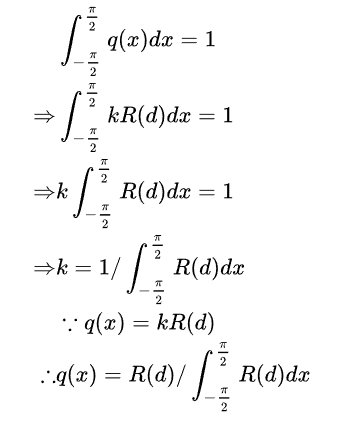
上式代入（1），有

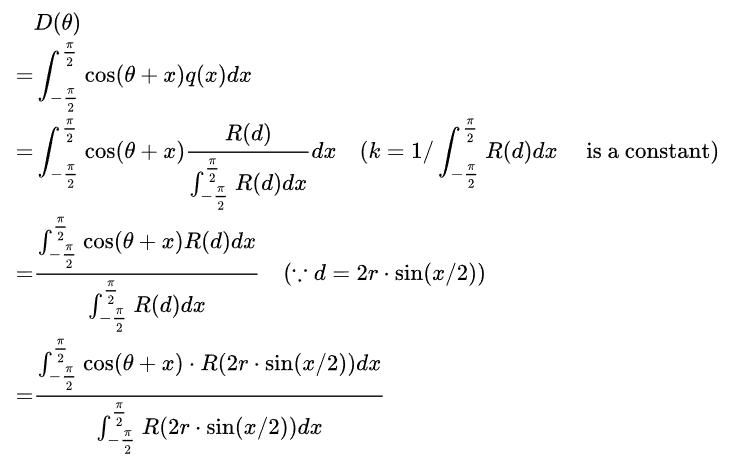
到这儿，就得推导出了开始的公式。

总结：1.得到能量守恒公式（2）的物理解释是关键；2. diffusion profile是基于距离的，不能用弧长代替弦长；3.对x的积分区域为（-pi/2， pi/2）；4.实践中，应该使cos（theta+x）大于0，因为光亮度不应该为负。

扩散剖面

上面提到了diffusion profile，gpu gem3这篇文章说出，高斯函数的和公式被用来近似扩散剖面。对每个扩散剖面R（r），我们用k个不同权重w，不同方差的高斯和表示：

变量v的高斯定义为

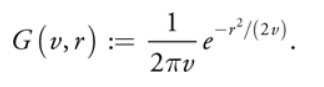
参考链接5中说，

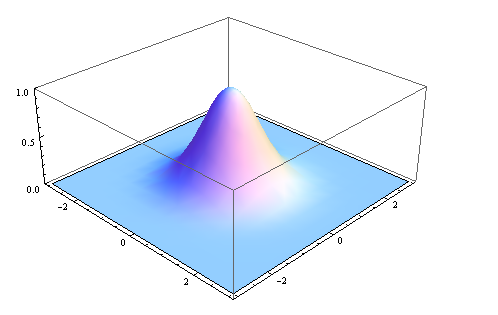
正态分布的密度函数叫做"高斯函数"（Gaussian function）。它的一维形式是：

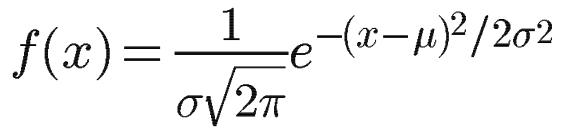
其中，μ是x的均值，σ是x的方差。因为计算平均值的时候，中心点就是原点，所以μ等于0。

根据一维高斯函数，可以推导得到二维高斯函数：

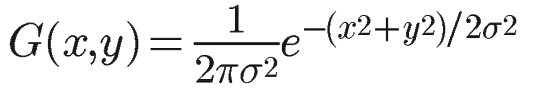
6个高斯的和能精确的模拟皮肤的三层模型。Gaussian参数如下，

6个高斯的方差是相同的，权重不同。r，g，b的权重不同。

看参考文档1中的代码

def G2(Neg_r_2, v):         
    v2 = 2.0 * v
    return 1.0/(v2 * math.pi) * math.exp(Neg_r_2/v2)

# Sum( w * G(v, r)  )
def Cal(distance,G):
    Neg_r_2 = -distance*distance
    rgb = array([0.233,0.455,0.649]) * G(Neg_r_2 , 0.0064)+\
          array([0.100,0.336,0.344]) * G(Neg_r_2 , 0.0484)+\
          array([0.118,0.198,0.000]) * G(Neg_r_2 , 0.1870)+\
          array([0.113,0.007,0.007]) * G(Neg_r_2 , 0.5670)+\
          array([0.358,0.004,0.000]) * G(Neg_r_2 , 1.9900)+\
          array([0.078,0.000,0.000]) * G(Neg_r_2 , 7.4100)
    return rgb

　　G2函数对应高斯公式，v是方差，Cal函数里的每个array代表r、g、b通道的不同权重。

这里求出来的颜色，正是上面D（theta）函数里的R（x），也就是某一点的散射率权重。

filmic-tonemapping

积分求出来后，需要进行filmic-tonemapping，参考这篇文章http://filmicworlds.com/blog/filmic-tonemapping-operators/，

将上面求出来的积分结果，进行如下计算：

float A = 0.15;
float B = 0.50;
float C = 0.10;
float D = 0.20;
float E = 0.02;
float F = 0.30;
float W = 11.2;

float3 Uncharted2Tonemap(float3 x)
{
   return ((x*(A*x+C*B)+D*E)/(x*(A*x+B)+D*F))-E/F;
}

float ExposureBias = 2.0f; float3 curr = Uncharted2Tonemap(ExposureBias*Color); float3 whiteScale = 1.0f/Uncharted2Tonemap(W); float3 color = curr*whiteScale; float3 retColor = pow(color,1/2.2); return float4(retColor,1);

　乘以255.

上面的结果乘以255，返回：

rgb = multiply(rgb,array([255,255,255]))
    return (int(rgb[0]),int(rgb[1]),int(rgb[2]))

　　运行python生成lut贴图

参考文档1中的python文件运行：安装python，安装pip，安装PIL库，安装numpy库(可参考这篇文章https://www.cnblogs.com/Shaojunping/p/11641778.html)，运行，生成lut。它的python代码里用的还是-pi到pi的积分(如果安装参考链接2所说，此处应该改成-pi/2, pi/2).

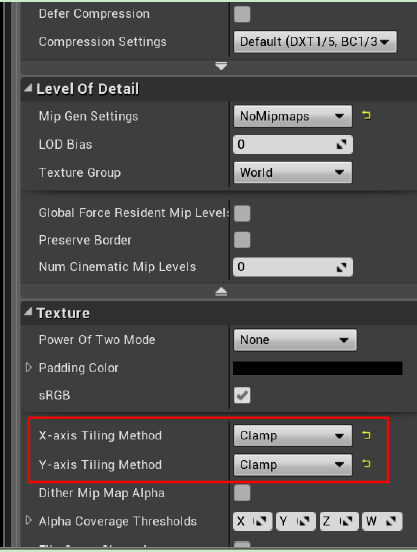
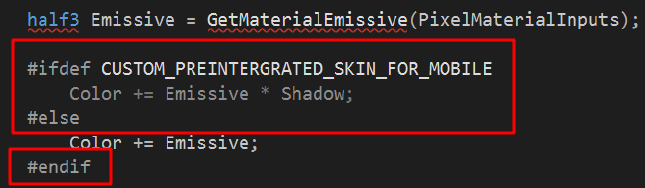
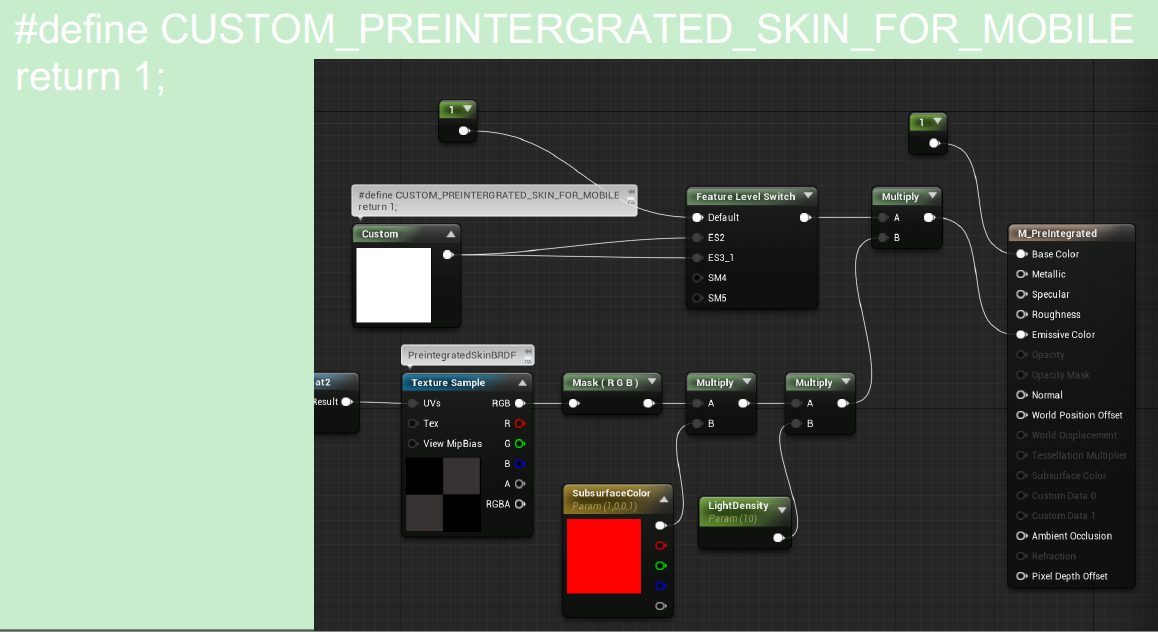
将生成的lut在ue4中使用：

参考uod2019，使用上面生成的lut贴图，加到材质的自发光上：

这张贴图的tiling 模式：

来源：https://www.cnblogs.com/Shaojunping/p/11643695.html

标签

lut