前言
实话是,我不知道自己学了多少遍了……感觉总有些模糊,于是写篇笔记总结一下。
后缀自动机是干啥的?
首先需要知道“自动机”的概念:
有限状态自动机的功能是识别字符串。
令一个自动机 \(A\) ,若它能识别字符串 \(S\) ,则令 \(A(S)=True\) ,否则 \(A(S)=False\)
自动机由五个部分组成——
\(alpha\) :字符集,\(state\) :状态集合,\(init\) :初始状态,\(end\) :结束状态集合,\(trans\) :状态转移函数。
而字符串 \(S\) 的 "后缀自动机" 的作用就是 识别 \(S\) 的所有子串。
这样有什么用呢?
可以掌握 \(S\) 的子串间的一些关系,从而解决问题,如“本质不同的子串数量”、“字符串的最小表示”等等。
而且由于后缀自动机有一些特殊性质,还可解决许多特殊问题。
更具体的,后缀自动机是干啥的?
在一个有向无环图(\(DAG\)) 上表示出 \(S\) 的所有子串。
这个 \(DAG\) 有一些性质:
- 有一个源点,若干个汇点,若干个普通节点。每条从一个节点指向另一节点的有向边上有一个字母。
- 从源点走到任一个汇点的任一条道路上的所有字母依次连起来,形成了 \(S\) 的一个后缀。
- 从源点走到任一个节点的任一条道路上的所有字母依次连起来,形成了 \(S\) 的一个子串。
- \(S\) 的所有子串都可通过 "3." 的方法走出来,且从源点出发,不同的道路形成的子串不同。
一种简单粗暴的实现
建一棵 \(trie\) 树,将 \(S\) 的所有后缀依次插入即可。
只是……时空都是 \(O(n^2)\) 级别的,伤不起伤不起。
于是我们需要尽可能缩小自动机的状态数和转移数。
\(so\) 出现了“后缀自动机” \(SAM\)
子串的一些性质
引入概念—— \(endpos\)
一个串 \(x\) 的 \(endpos\) 是 \(x\) 在字符串 \(S\) 中出现的结束位置的集合。
比方说,\(S=aababba\) ,\(x=ab\) ,那么 \(endpos(x)={3,5}\)
对于 \(endpos\) 相同的两个串,显然在 \(S\) 中,在它们后面可接的字符是一样的,即转移边相同。
把 \(endpos\) 相同的串称为一个等价类。
不妨在 \(SAM\) 中用同一个节点表示它们。
一些性质(比较显然,不证了):
对于任意两个子串 \(s1\) ,\(s2\) ,不妨设 \(length(s1)<length(s2)\)
- \(s1\) 为 \(s2\) 的后缀 \(\Leftrightarrow\) \(endpos(s1) \supseteq endpos(s2)\)
- \(s1\) 不为 \(s2\) 的后缀 \(\Leftrightarrow\) \(endpos(s1) \cap endpos(s2) = \emptyset\)
换句话说,\(s1\) 与 \(s2\) 的 \(endpos\) 间的关系只有两种,要么互不相交,要么一个包含于另一个。
SAM的组成
节点
前面已经提到过了,每一个节点表示 \(endpos\) 相同的所有串。
其实它表示的这些串就是从源点到该节点的所有不同路径形成的不同的子串。
由 \(endpos\) 的性质可证, 每个节点表示的所有串都互为连续的后缀关系
比如 \(S=aababba\) 中,\(endpos={7}\) 的子串有 \(aababba,ababba,babba,abba,bba\)
设每个节点 \(u\) 表示的最长子串为 \(Max(u)\), 最短子串为 \(Min(u)\)。
转移边与有向无环单词图
\(u\) 到 \(v\) 有一条字符为 \(c\) 的转移边,表示 \(u\) 代表的那些串加上字符 \(c\) 后形成的新串可用 \(v\) 代表。
注意, 这个单词图是个 \(DAG\) ,不一定 \(v\) 代表的所有子串都由 \(u\) 转移来
单词图的性质前面提到过了,再粘过来【捂脸】
从源点走到任一个节点的任一条道路上的所有字母依次连起来,形成了 \(S\) 的一个子串。
\(S\) 的所有子串都可这样走出来,且从源点出发,不同的道路形成的子串不同。
后缀链接与前缀树
“节点”处说到,“每个节点表示的所有串都互为连续的后缀关系”
不妨设 \(u\) 可表示的子串集合为 \(Substring(u)\) ,则任意 \(x \in Substring(u)\) ,满足 \(x\) 为 \(Max(u)\) 的后缀。
仍举上面的例子,\(S=aababba\) 中,\(endpos={7}\) 的子串有 \(aababba,ababba,babba,abba,bba\)
这5个子串只是 \(S\) 的后缀的一部分,还有 \(ba\) (\(endpos={4,7}\)) 和 \(a\) (\(endpos={1,2,4,7}\))
设表示 \(endpos={7}\) 的节点为 \(x\), 表示 \(endpos={4,7}\) 的节点为 \(y\),表示 \(endpos={1,2,4,7}\) 的节点为 \(z\)
那么连 后缀链接(或 \(pa\) 边)\(x \to y, y \to z\)
可以发现, \(u\) 的后缀链接连向 \(v\) ,当且仅当 \(|Min(u)|=|Max(v)|+1\) 且 \(v\) 表示的串全为 \(u\) 表示的串的后缀。
每个点的后缀链接只有一条,形成一个树结构,称这个树为 前缀树(或 \(Parent\) 树)
一些性质:
每个点沿着后缀链接往前跳,经过的节点表示的串长度变短,\(endpos\) 中包含的位置变多,最终跳到源点。
具体地:
对于 \(u \to v\) ,有 \(|Min(u)|=|Max(v)|+1\)
对于 \(u\) 可以跳到 \(v\) ,\(v\) 表示的串为 \(u\) 表示的串的后缀,\(endpos(u) \varsubsetneqq endpos(v)\)
SAM的构建
使用“增量法”构造,假设已有字符串 \(S\) 的 \(SAM\),现要添加、修改一些节点,形成 \(S+c\) 的\(SAM\)。
首先,\(SAM\) 的每个节点要存什么?
转移边、后缀链接和 \(|Max(u)|\)(为方便记,设其为 \(Len(u)\))。这些都要实时维护的。
struct node{
node *ch[26],*pa;
int len;
}pool[N*2],*root,*last;
其次,现在我们已有若干汇点,代表 \(S\) 的后缀。
我们要做的是为这些汇点找到表示字符 \(c\) 的转移边,并形成新的若干汇点。
这若干个汇点,相邻的是靠 后缀链接 连接的。
其中最后一个点 \(last\) 一定没有 \(c\) 的转移边,故新建一个节点 \(cur\) 代表 \(endpos={|S|+1}\) 的串,\(last\) 连 \(c\) 的转移边到 \(cur\) 。
依次往前的那些汇点,可能有一部分有 \(c\) 的转移边,有一部分没有。
但注意,假设 \(p\) 为第一个有该转移边的节点,那么它之前的节点一定都有 \(c\) 的转移边。(想一想,问什么)
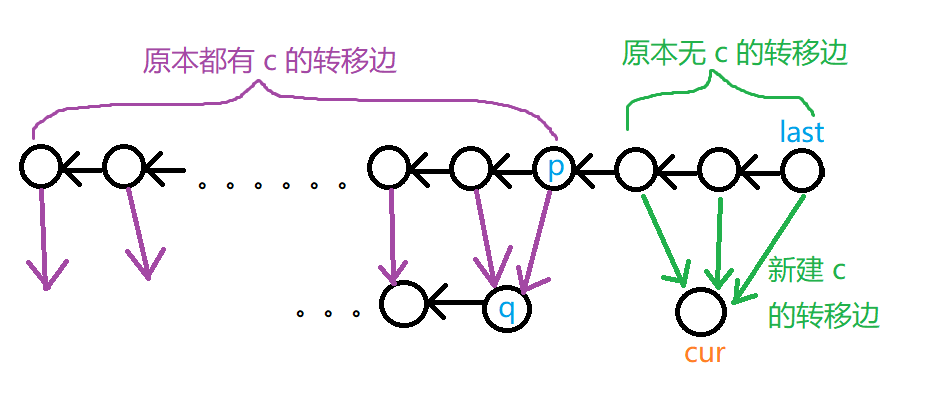
如图,对于原本无该转移边的节点,转移边 \(c\) 连向 \(cur\) 即可。
特殊情况,若这一条链中所有点都没有该转移边,直接 \(c\) 的后缀链接指向源点,结束。
此时所有能转移到 \(cur\) 的点都找齐了,也就能知道 \(Len(cur)=|S|+1\) ,\(|Min(cur)|=Len(p)+2\)
对从 \(p\) 开始往前的点,分情况考虑。设 \(p\) 的转移边 \(c\) 连向的点为 \(q\)。
情况一:\(Len(p)+1=Len(q)\)
直接把 \(cur\) 的后缀链接连向 \(q\) ,其他的都不用变。
(满足 \(|Min(cur)|=Len(p)+2=Len(p)+1+1=Len(q)+1=|Max(q)|+1\))
结束。
情况二: \(Len(p)+1<Len(q)\)
不满足 \(|Min(cur)|=|Max(q)|+1\) ,所以不能直接连后缀链接。
而应新建一个点 \(nq\) ,相当于 \(q\) 的复制点,将 \(q\) 的转移边复制到 \(nq\) 上。
使 \(Len(nq)=Len(p)+1\) ,让 \(cur\) 和 \(q\) 的后缀链接都连向 \(nq\) ,\(nq\) 的后缀链接连向 \(q\) 原先的后缀链接。
将原先转移边连向 \(q\) 的点,转移边连向 \(nq\)。
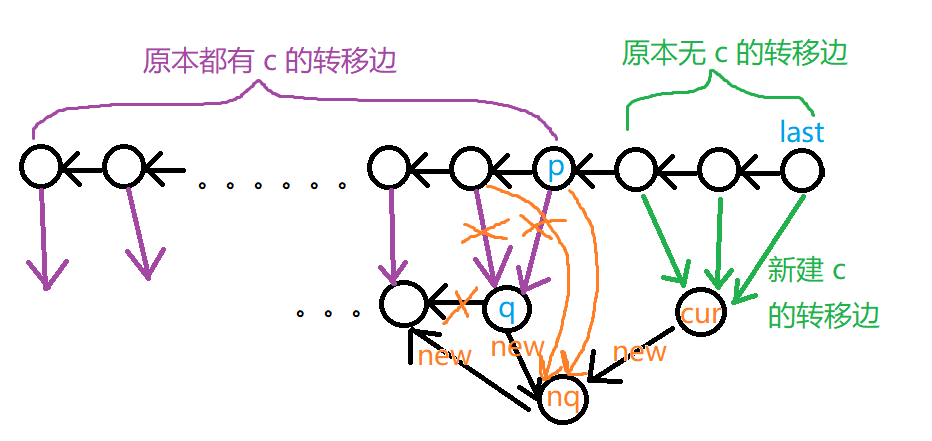
代码很简短。
void insert(int c){
node *p=last,*cur=&pool[++cnt];
cur->len=p->len+1;
for(;p && !p->ch[c];p=p->pa) p->ch[c]=cur;
if(!p) cur->pa=root;
else{
node *q=p->ch[c],*nq;
if(q->len==p->len+1) cur->pa=q;
else{
nq=&pool[++cnt];
nq->len=p->len+1;
for(int i=0;i<26;i++) nq->ch[i]=q->ch[i];
nq->pa=q->pa;
q->pa=cur->pa=nq;
for(;p && p->ch[c]==q;p=p->pa) p->ch[c]=nq;
}
}
last=cur;
}
复杂度证明
\(endpos\) 的等价类个数为 \(O(n)\)
边数为 \(O(n)\)
我犯懒了,参见这篇博客
反正是可证的,但要注意边数数组要开 \(2n\) 。
应用
且听下回分解。