1.Mini-batch 梯度下降（Mini-batch gradient descent)
batch gradient descent :一次迭代同时处理整个train data
Mini-batch gradient descent: 一次迭代处理单一的mini-batch (X{t} ,Y{t})
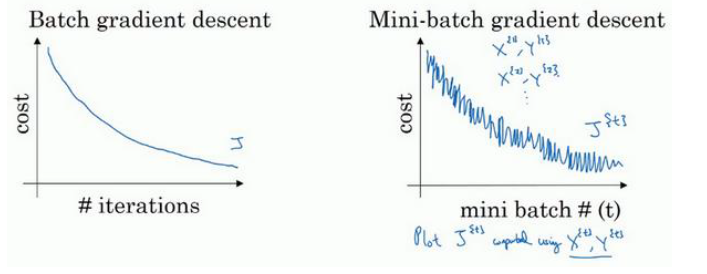
Choosing your mini-batch size : if train data m<2000 then batch ,else mini-batch=64~512 (2的n次方），需要多次尝试来确定mini-batch size
A variant of this is Stochastic Gradient Descent (SGD), which is equivalent to mini-batch gradient descent where each mini-batch has just 1 example. The update rule that you have just implemented does not change. What changes is that you would be computing gradients on just one training example at a time, rather than on the whole training set. The code examples below illustrate the difference between stochastic gradient descent and (batch) gradient descent.
- (Batch) Gradient Descent:
X = data_input
Y = labels parameters = initialize_parameters(layers_dims) for i in range(0, num_iterations): # Forward propagation a, caches = forward_propagation(X, parameters) # Compute cost. cost = compute_cost(a, Y) # Backward propagation. grads = backward_propagation(a, caches, parameters) # Update parameters. parameters = update_parameters(parameters, grads) - Stochastic Gradient Descent:
X = data_input
Y = labels parameters = initialize_parameters(layers_dims) for i in range(0, num_iterations): for j in range(0, m): # Forward propagation a, caches = forward_propagation(X[:,j], parameters) # Compute cost cost = compute_cost(a, Y[:,j]) # Backward propagation grads = backward_propagation(a, caches, parameters) # Update parameters. parameters = update_parameters(parameters, grads)
1 def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
2 """
3 Creates a list of random minibatches from (X, Y)
4
5 Arguments:
6 X -- input data, of shape (input size, number of examples)
7 Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
8 mini_batch_size -- size of the mini-batches, integer
9
10 Returns:
11 mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)
12 """
13
14 np.random.seed(seed) # To make your "random" minibatches the same as ours
15 m = X.shape[1] # number of training examples
16 mini_batches = []
17
18 # Step 1: Shuffle (X, Y)
19 permutation = list(np.random.permutation(m))
20 shuffled_X = X[:, permutation]
21 shuffled_Y = Y[:, permutation].reshape((1,m))
22
23 # Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
24 num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning
25 for k in range(0, num_complete_minibatches):
26 ### START CODE HERE ### (approx. 2 lines)
27 mini_batch_X = shuffled_X[:,k*mini_batch_size:(k+1)*mini_batch_size]
28 mini_batch_Y = shuffled_Y[:,k*mini_batch_size:(k+1)*mini_batch_size]
29 ### END CODE HERE ###
30 mini_batch = (mini_batch_X, mini_batch_Y)
31 mini_batches.append(mini_batch)
32
33 # Handling the end case (last mini-batch < mini_batch_size)
34 if m % mini_batch_size != 0:
35 ### START CODE HERE ### (approx. 2 lines)
36 mini_batch_X =shuffled_X[:,(k+1)*mini_batch_size:m]
37 mini_batch_Y =shuffled_Y[:,(k+1)*mini_batch_size:m]
38 ### END CODE HERE ###
39 mini_batch = (mini_batch_X, mini_batch_Y)
40 mini_batches.append(mini_batch)
41
42 return mini_batches2.指数加权平均数（Exponentially weighted averages):
指数加权平均数的公式：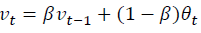
在计算时可视Vt 大概是1/(1-B)的每日温度，如果B是0.9，那么就是十天的平均值，当B较大时， 指数加权平均值适应更缓慢
指数加权平均的偏差修正：
3.动量梯度下降法（Gradinent descent with Momentum)
1 def initialize_velocity(parameters):
2 """
3 Initializes the velocity as a python dictionary with:
4 - keys: "dW1", "db1", ..., "dWL", "dbL"
5 - values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
6 Arguments:
7 parameters -- python dictionary containing your parameters.
8 parameters['W' + str(l)] = Wl
9 parameters['b' + str(l)] = bl
10
11 Returns:
12 v -- python dictionary containing the current velocity.
13 v['dW' + str(l)] = velocity of dWl
14 v['db' + str(l)] = velocity of dbl
15 """
16
17 L = len(parameters) // 2 # number of layers in the neural networks
18 v = {}
19
20 # Initialize velocity
21 for l in range(L):
22 ### START CODE HERE ### (approx. 2 lines)
23 v["dW" + str(l+1)] = np.zeros(parameters["W"+str(l+1)].shape)
24 v["db" + str(l+1)] = np.zeros(parameters["b"+str(l+1)].shape)
25 ### END CODE HERE ###
26
27 return v 1 def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
2 """
3 Update parameters using Momentum
4
5 Arguments:
6 parameters -- python dictionary containing your parameters:
7 parameters['W' + str(l)] = Wl
8 parameters['b' + str(l)] = bl
9 grads -- python dictionary containing your gradients for each parameters:
10 grads['dW' + str(l)] = dWl
11 grads['db' + str(l)] = dbl
12 v -- python dictionary containing the current velocity:
13 v['dW' + str(l)] = ...
14 v['db' + str(l)] = ...
15 beta -- the momentum hyperparameter, scalar
16 learning_rate -- the learning rate, scalar
17
18 Returns:
19 parameters -- python dictionary containing your updated parameters
20 v -- python dictionary containing your updated velocities
21 """
22
23 L = len(parameters) // 2 # number of layers in the neural networks
24
25 # Momentum update for each parameter
26 for l in range(L):
27
28 ### START CODE HERE ### (approx. 4 lines)
29 # compute velocities
30 v["dW" + str(l+1)] = beta*v["dW" + str(l+1)]+(1-beta)*grads["dW" + str(l+1)]
31 v["db" + str(l+1)] = beta*v["db" + str(l+1)]+(1-beta)*grads["db" + str(l+1)]
32 # update parameters
33 parameters["W" + str(l+1)] = parameters["W" + str(l+1)]-learning_rate*v["dW" + str(l+1)]
34 parameters["b" + str(l+1)] = parameters["b" + str(l+1)]-learning_rate*v["db" + str(l+1)]
35 ### END CODE HERE ###
36
37 return parameters, v
#β=0.9 is often a reasonable default.
4.RMSprop算法（root mean square prop）:
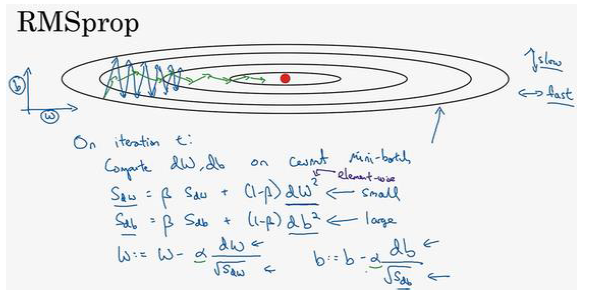
5.Adam 优化算法（Adam optimization algorithm)：
Adam 优化算法基本上就是将Momentum 和RMSprop结合在一起
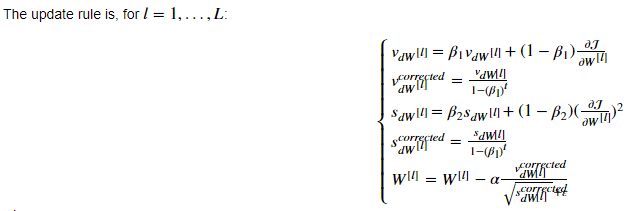
1 def initialize_adam(parameters) :
2 """
3 Initializes v and s as two python dictionaries with:
4 - keys: "dW1", "db1", ..., "dWL", "dbL"
5 - values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
6
7 Arguments:
8 parameters -- python dictionary containing your parameters.
9 parameters["W" + str(l)] = Wl
10 parameters["b" + str(l)] = bl
11
12 Returns:
13 v -- python dictionary that will contain the exponentially weighted average of the gradient.
14 v["dW" + str(l)] = ...
15 v["db" + str(l)] = ...
16 s -- python dictionary that will contain the exponentially weighted average of the squared gradient.
17 s["dW" + str(l)] = ...
18 s["db" + str(l)] = ...
19
20 """
21
22 L = len(parameters) // 2 # number of layers in the neural networks
23 v = {}
24 s = {}
25
26 # Initialize v, s. Input: "parameters". Outputs: "v, s".
27 for l in range(L):
28 ### START CODE HERE ### (approx. 4 lines)
29 v["dW" + str(l+1)] = np.zeros(parameters["W" + str(l+1)].shape)
30 v["db" + str(l+1)] = np.zeros(parameters["b" + str(l+1)].shape)
31 s["dW" + str(l+1)] = np.zeros(parameters["W" + str(l+1)].shape)
32 s["db" + str(l+1)] = np.zeros(parameters["b" + str(l+1)].shape)
33 ### END CODE HERE ###
34
35 return v, s 1 def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01,
2 beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8):
3 """
4 Update parameters using Adam
5
6 Arguments:
7 parameters -- python dictionary containing your parameters:
8 parameters['W' + str(l)] = Wl
9 parameters['b' + str(l)] = bl
10 grads -- python dictionary containing your gradients for each parameters:
11 grads['dW' + str(l)] = dWl
12 grads['db' + str(l)] = dbl
13 v -- Adam variable, moving average of the first gradient, python dictionary
14 s -- Adam variable, moving average of the squared gradient, python dictionary
15 learning_rate -- the learning rate, scalar.
16 beta1 -- Exponential decay hyperparameter for the first moment estimates
17 beta2 -- Exponential decay hyperparameter for the second moment estimates
18 epsilon -- hyperparameter preventing division by zero in Adam updates
19
20 Returns:
21 parameters -- python dictionary containing your updated parameters
22 v -- Adam variable, moving average of the first gradient, python dictionary
23 s -- Adam variable, moving average of the squared gradient, python dictionary
24 """
25
26 L = len(parameters) // 2 # number of layers in the neural networks
27 v_corrected = {} # Initializing first moment estimate, python dictionary
28 s_corrected = {} # Initializing second moment estimate, python dictionary
29
30 # Perform Adam update on all parameters
31 for l in range(L):
32 # Moving average of the gradients. Inputs: "v, grads, beta1". Output: "v".
33 ### START CODE HERE ### (approx. 2 lines)
34 v["dW" + str(l+1)] = beta1* v["dW" + str(l+1)]+(1-beta1)*grads["dW" + str(l+1)]
35 v["db" + str(l+1)] = beta1* v["db" + str(l+1)]+(1-beta1)*grads["db" + str(l+1)]
36 ### END CODE HERE ###
37
38 # Compute bias-corrected first moment estimate. Inputs: "v, beta1, t". Output: "v_corrected".
39 ### START CODE HERE ### (approx. 2 lines)
40 v_corrected["dW" + str(l+1)] = (v["dW" + str(l+1)])/(1-np.power(beta1,t))
41 v_corrected["db" + str(l+1)] = (v["db" + str(l+1)])/(1-np.power(beta1,t))
42 ### END CODE HERE ###
43
44 # Moving average of the squared gradients. Inputs: "s, grads, beta2". Output: "s".
45 ### START CODE HERE ### (approx. 2 lines)
46 s["dW" + str(l+1)] = beta2* s["dW" + str(l+1)]+(1-beta2)*np.power(grads["dW" + str(l+1)],2)
47 s["db" + str(l+1)] = beta2* s["db" + str(l+1)]+(1-beta2)*np.power(grads["db" + str(l+1)],2)
48 ### END CODE HERE ###
49
50 # Compute bias-corrected second raw moment estimate. Inputs: "s, beta2, t". Output: "s_corrected".
51 ### START CODE HERE ### (approx. 2 lines)
52 s_corrected["dW" + str(l+1)] = s["dW" + str(l+1)]/(1-np.power(beta2,t))
53 s_corrected["db" + str(l+1)] = s["db" + str(l+1)]/(1-np.power(beta2,t))
54 ### END CODE HERE ###
55
56 # Update parameters. Inputs: "parameters, learning_rate, v_corrected, s_corrected, epsilon". Output: "parameters".
57 ### START CODE HERE ### (approx. 2 lines)
58 parameters["W" + str(l+1)] = parameters["W" + str(l+1)]-learning_rate*v_corrected["dW" + str(l+1)]/(s_corrected["dW" + str(l+1)]+epsilon)
59 parameters["b" + str(l+1)] = parameters["b" + str(l+1)]-learning_rate*v_corrected["db" + str(l+1)]/(s_corrected["db" + str(l+1)]+epsilon)
60 ### END CODE HERE ###
61
62 return parameters, v, s
6.学习率衰减（Learning rate decay):
加快学习算法的一个办法就是随时间慢慢减少学习率，这样在学习初期，你能承受较大的步伐，当开始收敛的时候，小一些的学习率能让你步伐小一些。
综合练习：
1 def model(X, Y, layers_dims, optimizer, learning_rate = 0.0007, mini_batch_size = 64, beta = 0.9,
2 beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8, num_epochs = 10000, print_cost = True):
3 """
4 3-layer neural network model which can be run in different optimizer modes.
5
6 Arguments:
7 X -- input data, of shape (2, number of examples)
8 Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
9 layers_dims -- python list, containing the size of each layer
10 learning_rate -- the learning rate, scalar.
11 mini_batch_size -- the size of a mini batch
12 beta -- Momentum hyperparameter
13 beta1 -- Exponential decay hyperparameter for the past gradients estimates
14 beta2 -- Exponential decay hyperparameter for the past squared gradients estimates
15 epsilon -- hyperparameter preventing division by zero in Adam updates
16 num_epochs -- number of epochs
17 print_cost -- True to print the cost every 1000 epochs
18
19 Returns:
20 parameters -- python dictionary containing your updated parameters
21 """
22
23 L = len(layers_dims) # number of layers in the neural networks
24 costs = [] # to keep track of the cost
25 t = 0 # initializing the counter required for Adam update
26 seed = 10 # For grading purposes, so that your "random" minibatches are the same as ours
27
28 # Initialize parameters
29 parameters = initialize_parameters(layers_dims)
30
31 # Initialize the optimizer
32 if optimizer == "gd":
33 pass # no initialization required for gradient descent
34 elif optimizer == "momentum":
35 v = initialize_velocity(parameters)
36 elif optimizer == "adam":
37 v, s = initialize_adam(parameters)
38
39 # Optimization loop
40 for i in range(num_epochs):
41
42 # Define the random minibatches. We increment the seed to reshuffle differently the dataset after each epoch
43 seed = seed + 1
44 minibatches = random_mini_batches(X, Y, mini_batch_size, seed)
45
46 for minibatch in minibatches:
47
48 # Select a minibatch
49 (minibatch_X, minibatch_Y) = minibatch
50
51 # Forward propagation
52 a3, caches = forward_propagation(minibatch_X, parameters)
53
54 # Compute cost
55 cost = compute_cost(a3, minibatch_Y)
56
57 # Backward propagation
58 grads = backward_propagation(minibatch_X, minibatch_Y, caches)
59
60 # Update parameters
61 if optimizer == "gd":
62 parameters = update_parameters_with_gd(parameters, grads, learning_rate)
63 elif optimizer == "momentum":
64 parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)
65 elif optimizer == "adam":
66 t = t + 1 # Adam counter
67 parameters, v, s = update_parameters_with_adam(parameters, grads, v, s,
68 t, learning_rate, beta1, beta2, epsilon)
69
70 # Print the cost every 1000 epoch
71 if print_cost and i % 1000 == 0:
72 print ("Cost after epoch %i: %f" %(i, cost))
73 if print_cost and i % 100 == 0:
74 costs.append(cost)
75
76 # plot the cost
77 plt.plot(costs)
78 plt.ylabel('cost')
79 plt.xlabel('epochs (per 100)')
80 plt.title("Learning rate = " + str(learning_rate))
81 plt.show()
82
83 return parameters
来源：oschina
链接：https://my.oschina.net/u/4340851/blog/3712964