我们在训练机器学习模型的时候一般会使用随机梯度下降(SGD)。但SGD有个显著的缺点,那就是到了后期loss会起起伏伏,令我们炼丹师头秃。这个现象其实在深度学习之前的凸问题上就有了,这次介绍
1. 为什么我们在大数据下偏爱SGD;
2. 为什么SGD会不稳、不快;
3. 让SGD更快的一个典型方法——SVRG。
这篇文章来源是这样的:前面的SGD直观解释部分主要是参考本专栏之前的一篇文章[0],后面的SGD公式推导和SVRG部分主要是参考了香港科技大学张潼老师的优化课程的内容,写在这里相当于一个小笔记吧。
本文分成一下几个部分:
Part I: SGD简介
Part II: SGD的方差以及造成的影响
Part II.A: 直观描述
Part II.B: 公式描述、逐渐缩小的步长
Part III: 如何减小SGD的方差——SVRG
如果有啥没有说对的欢迎指出来,因为能力有限,也没有做过SGD相关工作,所以如果有哪里错了请一定指出来免得误导大家。
Part I: SGD简介
在机器学习的问题当中,我们一般要解决的问题长这个样子
其中呢, 是要优化的weights,
就代表了一个个的样本。
梯度下降长这个样子
我们看看这个表达式,它其实并不适合我们今天的“大数据”,因为每次更新的时候都要算一遍所有样本的梯度,如果数据量大了(比如几百万条),这个操作是很耗时间的。由于这种大数据的需求,就有了随机梯度下降,我每次从样本当中采样一条或者几条,然后进行一次梯度下降,这里简单起见就采一条吧
从理论分析上来看呢,SGD在计算复杂度上是可能有好处的

为了有一个直观的比较,我画了一张SGD和GD最小二乘法下的图。
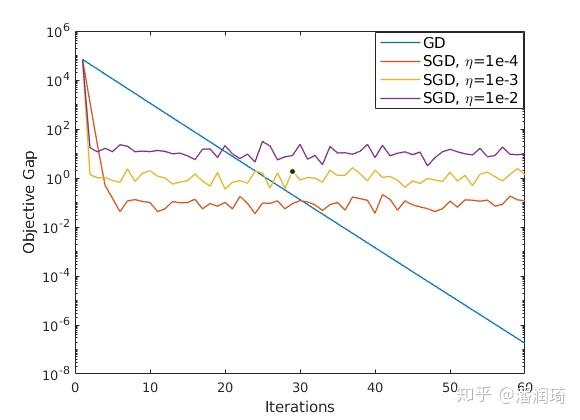
从图中可以看出,在前期精度要求不高的时候,SGD的优势还是比较大的,在后期SGD就慢慢水了下来。步长越大前期越快后期也越水。所以在精度要求不高数据量大的问题里面,SGD的优势还是很明显的。
Part II: SGD的方差以及造成的影响
Part II.A: 直观描述
在从上面的图里面我们可以看出,SGD在前期是很棒的,但是后期就水了起来,这是什么原因呢?这里用[0]里面的描述。
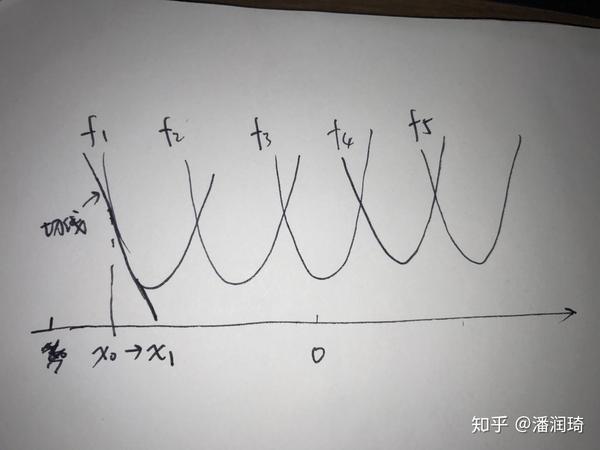
我们首先从直观上描述一下这个问题,假设我们要优化一个二次函数,有五个sample,长这个样子
其中 。
在前期的时候呢,梯度一直是朝着0方向前进的,所以下降是很快的,就像下面这张图
而到了后期,我们离最优解“0”的距离很近,有一些梯度向着0走,有一些梯度远离0走,就像下面这张图
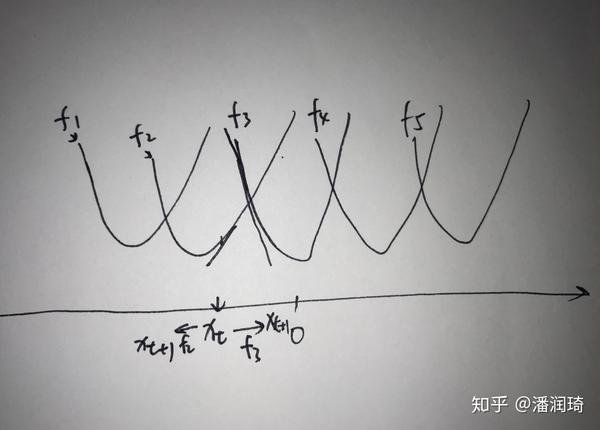
因为每次采样一个样本,我们可能采样到 从而离最优点更近,也可能采样到
离最优点更远,忽远忽近,在收敛图表现为波动,loss卡在了某个点下不去。
Part II.B: 公式描述
上面的介绍给了一个直观上的描述,那要怎么做才能克服这个问题呢,还是要先把问题用数学语言描述然后再去解决。我们顺着GD的推导尝试一下推导一下SGD的收敛性,看看到底是哪里出问题了(这里假设L-smooth -strongly convex)。
我们先看下GD的收敛性,回顾一下L-smooth的条件
我们把 代入到(3)里面就是
回顾一下strongly convex的条件
,我们有
所以有
取
下面顺着这个思路对SGD进行推导,把
两边对i取期望
其中第一项期望呢
我们可以看到和GD的(4)里面一毛一样。我们下面想把第二项期望 也写成(4)里面的形式也就是
,这样也可以依葫芦画瓢得到SGD的收敛性。第二个期望稍微有点难搞,我们定义一个梯度的方差,令
,把V用平方差公式展开有
化简一下就是
把(7)和(8)代入到(6)里面呢,就是
比较一下(9)和(4)呢,我们发现多了一项 ,因为有这一项的存在,固定步长的SGD的loss会卡在某一个点,并且步长越大卡在的那个点离最优点也就越远,这就解释了上面那张最小二乘法实验的现象。
那么如何解决这个问题呢,我们尝试取一个步长使得(9)右边最小
因为这是一个关于
随着迭代次数的增加,因为最优点 所以
,因为最优点并不是每个样本的梯度都是0(
)所以V并不会趋于0。综上,最优的步长
选取是一个逐渐趋于0的步长 。做一下最小二乘法的实验发现用固定步长会卡在某个点,逐渐趋于0的步长会一直下去。
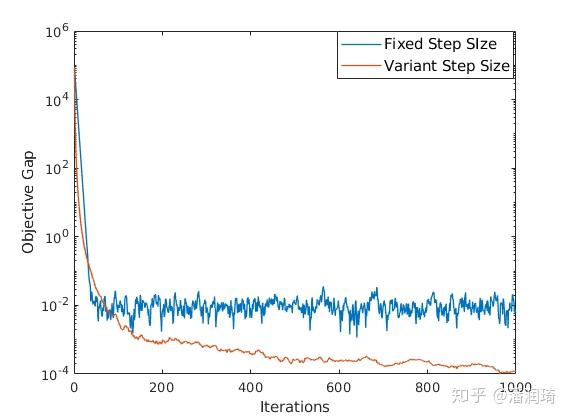
这也是我们在炼丹的时候需要过段时间减小一下step size的原因。但步长逐渐趋于0也带来了一个问题,就是到后面走得越来越少,收敛越来越慢,最快也只能达到 的收敛速度[1](证明在[1]的25-26页),并不能达到指数收敛,所以到大后期还是很水。

Part III: 如何减小SGD的方差——SVRG
那要怎么做才能使得收敛速度超过 呢,那就得用更长的步长。想想梯度下降有两个参数,一个是方向,一个是步长。既然我们得用比较大的步长,那我们就改下降的方向让(10)里面的V也趋于0就行了,这也是SVRG的想法。
在SVRG当中我们每隔m次迭代留一下自变量 估计一下整体的梯度
定义一个新的函数
也可以写成
的求和形式,即
SVRG每次sample一个
直观理解一下,在非常靠近最优点的地方有
计算一下呢就是(详细的计算过程在[2]的第四页的(8)的下面几行)
趋于
,V也会趋于0,这就允许了我们采用一个更加aggressive的步长。SVRG具体算法是这个样子的

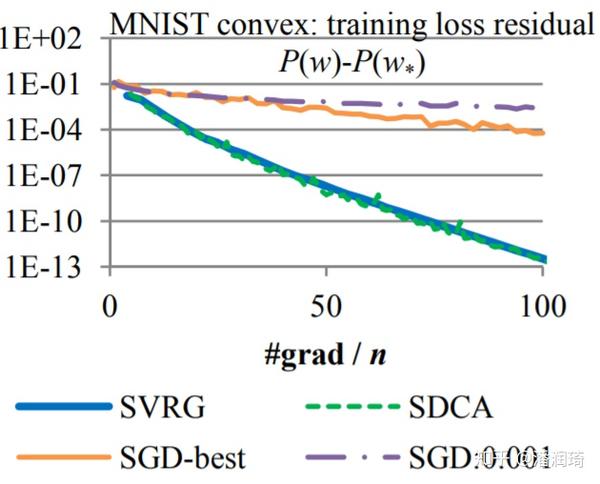
可以证明SVRG在smooth strongly convex情况下可以指数收敛,证明也也非常简洁只有一页纸([2]的第四页)。

实验图长这个样子,我们看到它的收敛速度远远快于SGD。
总结一下就是
- 在样本数量大的时候SGD比GD有优势;
- SGD前期很快,但后期因为方差大所以变水了,可以通过调小步长让loss进一步下降;
- SVRG通过gradient aggragation减小方差使得SGD更快收敛。
最后欢迎大家关注专栏 非凸优化学习之路,这里还有更多的关于优化的和面试的小知识。
也欢迎关注我的新专栏 图神经网络实战,这里会更新GNN最新的paper以及代码解读。
[1] Stochastic gradient methods
[2] Accelerating Stochastic Gradient Descent using Predictive Variance Reduction
来源:oschina
链接:https://my.oschina.net/u/4380417/blog/4428209