自己动手写一个简单正则表达式解析器(待续，未完成)

1.状态机及形式语言基础

2. 版本1：仅仅匹配一个？

3. 版本2：如何匹配*？

4. 如何实现*, ?的匹配？

5. 如何实现根据输入的pattern，生成DFA状态机？

1. 状态机及形式语言基础

1.1 语言和文法

在计算机中存在下面两个比较重要的问题，一个问题提出之后，能否使用计算机来执行，如果能够执行的话，那么该怎么执行？这些都是计算模型需要解决的问题，为解决山这些问题，需要来首先了一下什么是形式语言，相对于自然语言而言，如何去描述一个形式语言(文法)？

自然语言就是日常的口头语言，将一个自然语言翻译成另外的一种自然语言的问题引出了“形式语言”的概念。下面就是一个迭代的定义：

1. 字母表V：含有有限元素的非空集合，其中包含终结符号（无法被替换的符号）记为T；非终结符号（简单的将是能够被替换的元素），记为N;定义开始符S为推导的开始。

2. 单词：定义在字母表V上的单词定义为V中元素组成的有限长度的字串。

3. 空串：没有符号的串，记为λ

4. V上所有单词的集合记为V* 

5. 指明V*中的串能够被什么样的串替换的表达式称之为“产生式”

6. 有了上面的基础开始定义什么是文法：文法是由下面的是是部分组成：G = < V, T, S, P >，其中字母表V，有V上的所有的终结符组成的集合T，S为推导的开始符，P为产生式的集合。

7. 下面定义什么是语言L，由G生成的语言是由S能够推导出的所有终结符号构成的集合。

显然通过上面的定义同时类比自然语言：字母表相当于英语的26个字母。单词类似于自然语言的英语单词；文法就相当于英语的语法规则，例如(名词 + 动词 + 形容词, i am happy)。通过这些文法进而能够推导出英语的一系列句子，即是语言。这是一个简单的例子：

定义词汇表V ={S, A, a, b}，定义终结符号T = { a, b }，开始符号定义为S，产生式如下：

 S -> aA S -> b A -> aa，那么通过上述文法说能够表达的语言的集合如下：

 S -> aA -> aaa这是语言的其中之一，另外S -> b是另外一个，所以L(G) = { b, aaa }

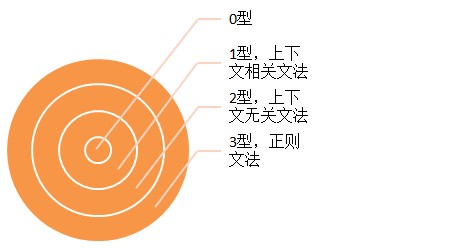
1.2 文法的分类

文法存在着多种分类方式，常见的是乔姆斯基分类方法。该方法将文法分为0型文法：对产生式没有要求；1型文法，存在两种产生式w1->w2，且|w1| > |w2|，或者是w1->λ；2型文法，只存在w1->w2的表达式，并且w1是一个非终结符的单个符号;3型文法，只存在w1->w2的形式，并且满足w1=A, 并且w2=aB或者w2=a，或者满足w1=S, w2=λ.通过上面的定义可以看出要求是越来越严格。其中1型文法也称之为上下文相关文法（如果想要使用某个产生是进行推导的话，必须要根据推导公式的上下文），2型文法同时也称为上下文无关文法。

 

1.3 有限状态机简介

1.3.1 定义

 有限状态机M={S, I, O, f, g, s0}

S：有限状态集合

I：输入字母表

O:  输出字母表

f：状态转换函数

g：输出函数

s0：初始状态 

状态机可以使用状态转换图或者是状态转换表来表示，状态转换图比较直观，状态转换表的话，比较容易编写程序。

1.3.2 NFA

NFA表示对于某个状态state和输出input的话，NFA的下一个状态不唯一 ，而是存在形成一个状态集合。

1.3.3 DFA

 和NFA不同在于，DFA的下一个状态是唯一的。 

1.3.4 如何将正则表达式转换成NFA？

只需按照下面的方法(Thompson)，即可将正则表达式转换成NFA（http://tech.idv2.com/2006/05/08/parse-regex-with-DFA/）:

1. 对于空记号ε，生成下面的NFA

 

2. 对于V的字母表中的元素a，生成下面的NFA

 

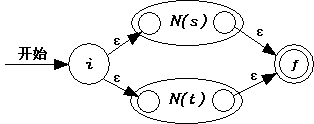
3.  令正则表达式s和t的NFA分别为N(s)和N(t) 

3.1  对于s|t，按照以下的方式生成NFA N(s|t)

 

3.2  对于st，按照以下的方式生成NFA N(st)

 

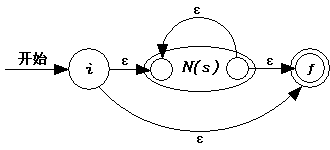
3.3 对于s*，按照以下的方式生成NFA N(s*) 

 

3.4 对于(s)，使用s本身的NFA N(s) 

下面是一个具体的例子：

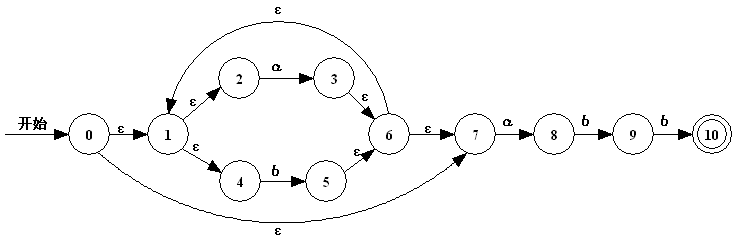
正则表达式r=(a|b)*abb转换成NFA之后，如下：

 

1.3.5 如何将NFA转换成DFA？ 

输入 NFA N

输出 能够接受与N相同语言的DFA D

方法本算法生成D对应的状态迁移表Dtran。DFA的各个状态为NFA的状态集合， 对于每一个输入符号，D模拟N中可能的状态迁移。

 

定义以下的操作。

操作 说明

ε-closure(s) 从NFA的状态s出发，仅通过ε迁移能够到达的NFA的状态集合

ε-closure(T) 从T中包含的某个NFA的状态s出发，仅通过ε迁移能够到达的NFA的状态集合

move(T, a) 从T中包含的某个NFA的状态s出发，通过输入符号a迁移能够到达的NFA的状态集合

 

令 Dstates 中仅包含ε-closure(s), 并设置状态为未标记;

while Dstates中包含未标记的状态T do

begin

  标记T;

  for 各输入记号a do

  begin

    U := ε-closure(move(T, a));

    if U不在Dstates中 then

      将 U 追加到 Dstates 中，设置状态为未标记;

    Dtrans[T, a] := U;

  end

end

ε-closure(T)的计算方法如下：

将T中的所有状态入栈;

设置ε-closure(T)的初始值为T;

while 栈非空 do

begin

  从栈顶取出元素t;

  for 从t出发以ε为边能够到达的各个状态u do

    if u不在ε-closure(T)中 then

    begin

      将u追加到ε-closure(T)中;

      将u入栈;

    end

end 

1.4 如何进行语言识别简单通用模块？程序代码块结构。

基本的代码（示意代码，不准确）块如下：根据上面的状态机定义，首先定义初始状态state，定义输入ch，开始循环，如果没有到结尾，开始状态转换。

 

2. 版本1，如何识别一个？

---

 // 简单正则表达式匹配函数

#include <iostream>

using namespace std;

// 匹配函数，仅仅是实现？的匹配，并且假定现在的

// pattern是固定的“a?b”，其中?可以匹配任意一个字符

bool match1(char* essay, char* pattern)

{

    // 定义初始状态

    int state = 0;

    int i = 0;  // essay中的游标

    char ch;    // essay中的下一个字符

    int firstMatch = -1;

    while(true)

    {

        ch = essay[i];

        if (ch == '\0') // 字符串结尾

            return false;

        // 状态转换函数，控制i的移动

        if ( (state == 0) && (ch == 'a') )

        {

            state = 1;   // 状态1

            firstMatch = i;

            ++i;

        }

        else if( (state == 1) )  // 任意字符

        {

            state = 2;   // 状态2

            ++i;

        }

        else if( (state == 2) && (ch == 'b') )

        {

            state = 3;  // 状态3，表明是最终状态

            ++i;

        }

        else if (state != 0)    // 回退

        {

            state = 0;

            // 将游标回退

            i = firstMatch + 1;

        }

        else

        {

            state = 0;

            ++i;

        }

        if (state == 3) // 最终状态

            return true;

    }

}

int main()

{

    ////////////////////手动构造自动机/////////////

    // 定义变量

    char* essay =  "aadfgdfgdfgdgdfgasbfb";

    char* pattern = "a?b";

    // 调用匹配函数

    bool found = match1(essay, pattern);

    cout << ( found ? "found" : "not found" ) << endl;

    ///////////////////////////////////////////////

    return 0;

}

---

 

来源：https://www.cnblogs.com/xuqiang/archive/2011/03/25/1995542.html