蓝桥杯算法练习笔记(13)__背包问题

14.背包问题

1.0-1背包问题

例如：有5件物品，体积分别为[2,2,6,5,4]，价值分别为[6,3,5,4,6]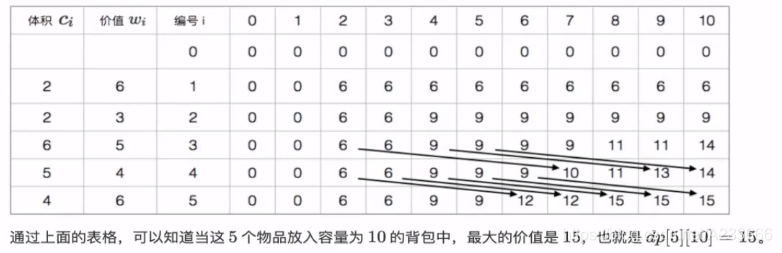

//0-1背包问题
#include<iostream>
#include<cstdio>
using namespace std;

int c[105];//每件物品的体积
int w[105];//每件物品的价值
int dp[105][105]; 

int main(){
	
	int n,v;//n件物品 最大可用体积为v 
	cin>>n>>v;
	for(int i=1;i<=n;i++){
		cin>>w[i]>>c[i];
	}
	
	for(int i=1;i<=n;i++){ //前i个物品
		for(int j=0;j<=v;j++){ //总重量不超过j
			if(j>=c[i]){ // 最大价值 dp[i][j]
				dp[i][j]=max(dp[i-1][j-c[i]]+w[i],dp[i-1][j]);
			}else{ //不放，继承上一次数据
				dp[i][j]=dp[i-1][j];
			}
		}
	}
	 
	cout<<dp[n][v]<<endl;
	return 0;
} 

/*
--cin: 
5 10 //数量 体积 
2 1 //单件价值 重量 
3 5
2 5
3 4
4 3
--cout: //最大价值 
9
*/

//空间/时间复杂度 O(VN)

#include<iostream>
#include<cstdio>
using namespace std;

int dp[1005];
int w[105],c[105];

int main(){
	int n,v;
	cin>>n>>v;
	for(int i=1;i<=n;i++){
		cin>>w[i]>>c[i];
	}
	for(int i=1;i<=n;i++){
		for(int j=v;j>=c[i];j--){
			dp[j]=max(dp[j-c[i]]+w[i],dp[j]);
		}
	}
	cout<<dp[v]<<endl;
	return 0;
}
/*
--cin:
5 10
6 2
3 2
5 6
4 5
6 4
--cout:
15
*/

// 01背包问题魔改
/* 用 价值/体积 得到单位体积物品的价值量
   并 从高到低 进行排序，在总体积允许的范围内
   尽可能选择 单位价值 更高的物品 
*/ 
#include<iostream>
#include<algorithm>
using namespace std;

struct Bao{
	int w;//价值 
	int c;//体积
};

double cmp(Bao a,Bao b){ // 价值/体积 升序 
	return a.w/a.c>b.w/b.c;
}

int main(){
	int n,v;
	cin>>n>>v;
	Bao bao[n];
	for(int i=0;i<n;i++){
		cin>>bao[i].w>>bao[i].c;
	} 
	sort(bao,bao+n,cmp);
	
	int sumw=0,sumc=0;
	for(int i=0;i<n;i++){
		int tc=sumc+bao[i].c;
		int tw=sumw+bao[i].w;
		if(tw>sumw && tc<v){
			sumw=tw;
			sumc=tc;
		}
	}
	
	cout<<sumw<<endl;
	
	return 0;
}

2.多重背包

有N种物品，第i种物品的体积是Ci ，价值是Wi，每种物品有 Ni 件，有体积为V的背包，求最大价值

01背包就是特殊的多重背包（多重背包里面Ni件物品相当于01背包中Ni件相同的物品）

//多重背包
#include<iostream>
#include<cstring>
using namespace std;

int dp[21][1010];
int w[21],c[21],n[21];

int main(){
	int N,V;
	cin>>N>>V;
	for(int i=1;i<=N;i++){
		cin>>w[i]>>c[i]>>n[i];
	}
	for(int i=1;i<=N;i++){
		for(int j=0;j<=V;j++){
			for(int k=0;k<=n[i];k++){
				if(j>=c[i]*k){
					dp[i][j]=max(dp[i-1][j-c[i]*k]+w[i]*k,dp[i][j]);
				}
			}
		}
	}
	
	cout<<dp[N][V]<<endl;
	return 0;
}
/*
--cin:
5 10 // N V 
2 1 2 //价值，体积，个数 
3 5 3
2 5 1
3 4 2
4 3 8
--cout:
14
----
取 体积为3 价值为4的 3个
取 体积为1 价值为2的 1个
*/

//多重背包--空间优化 
#include<iostream>
#include<cstring> 
using namespace std;

int dp[1010]; 
int w[21],c[21],n[21];
int main(){
	int N,V;
	cin>>N>>V;
	for(int i=1;i<=N;i++){
		cin>>w[i]>>c[i]>>n[i]; 
	}
	for(int i=1;i<=N;i++){
		for(int j=V;j>=0;j--){
			for(int k=0;k<=n[i];k++){
				if(j>=c[i]*k){
					dp[j]=max(dp[j-c[i]*k]+w[i]*k,dp[j]);
				}
			}
		}
	}
	cout<<dp[V]<<endl;
	return 0; 
}

3.完全背包

当前有N中物品，第i中物品的体积是Ci ，价值是 Wi

每种物品的数量是无限的，可以选若干件，

有容量为 V 的背包，求最大价值

#include<iostream>
#include<cstring>
using namespace std;

int dp[21][1010];
int w[21],c[21];

int main(){
	int N,V;
	cin>>N>>V;
	for(int i=1;i<=N;i++){
		cin>>w[i]>>c[i]; 
	}
	for(int i=1;i<=N;i++){
		for(int j=0;j<=V;j++){
			if(j>=c[i]){
				dp[i][j]=max(dp[i][j-c[i]]+w[i],dp[i-1][j]);
			}else{
				dp[i][j]=dp[i-1][j];
			}
		}
	}
	
	cout<<dp[N][V]<<endl;
	return 0;
} 

/*
--cin:
5 10
2 1
3 5
2 5
3 4
4 3
--cout:
20

*/

#include<iostream>
#include<cstring>
using namespace std;

int dp[1010];
int w[21],c[21];

int main(){
	int N,V;
	cin>>N>>V;
	for(int i=1;i<=N;i++){
		cin>>w[i]>>c[i]; 
	}
	//空间优化 
	for(int i=1;i<=N;i++){
		for(int j=c[i];j<=V;j++){
			dp[j]=max(dp[j-c[i]]+w[i],dp[j]);
		}
	}
	
	cout<<dp[V]<<endl;
	return 0;
} 

4.二进制优化多重背包

//多重背包的二进制优化 
#include<iostream>
using namespace std;
int n[110],c[110],w[110];
int nc[1000],nw[1000];
int dp[5010]; 
int main(){
	int N,V;
	cin>>N>>V;
	for(int i=1;i<=N;i++){
		cin>>w[i]>>c[i]>>n[i];
	}
	int ncnt=0;
	for(int i=1;i<=N;i++){
		int k;
		for(k=1;n[i]-(1<<k)+1>0;++k){
			nc[ncnt]=(1<<(k-1))*c[i];
			nw[ncnt]=(1<<(k-1))*w[i];
			++ncnt;
		}
		--k;
		nc[ncnt]=(n[i]-(1<<k)+1)*c[i];
		nw[ncnt]=(n[i]-(1<<k)+1)*w[i];
		++ncnt;
	}
	for(int i=0;i<ncnt;++i){
		for(int j=V;j>=nc[i];--j){
			dp[j]=max(dp[j],dp[j-nc[i]]+nw[i]);
		}
	}
	cout<<dp[V]<<endl;
	
	return 0;
}
/*
--cin:
5 10
2 1 2
3 5 3
2 5 1
3 4 2
4 3 8
--cout:
14
*/

来源：CSDN

作者：耿鬼不会笑

链接：https://blog.csdn.net/A233666/article/details/104835952