SVM是英文Support Vector Machine首字母缩写,中文名支持向量机。
是机器学习领域最顶尖的存在,应用领域广、预测效果好,被誉为万能分类器,正是这样,SVM的理解和学习也比其他的算法要难一些。也是本人数据挖掘专栏的终结篇。
为了能更好的让大家理解,这里我们对里面设计的知识点进行分解处理,所以在真正学习SVM之前,先介绍一下向量与平面、拉格朗日乘子法。
目录
一、向量与平面
1、向量
对于一个向量a,只需要关心它的方向和大小(长短),即终点坐标-起点坐标,不需要关心位置。
假设有两个向量a,b
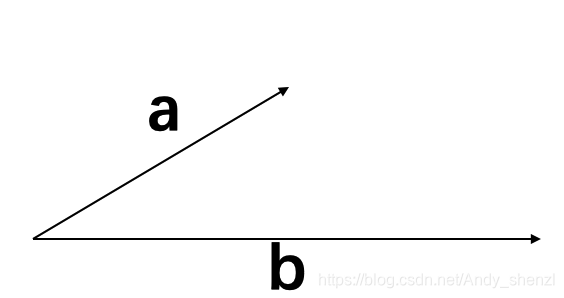
a=(a1,a2)
b= (b1,b2)
根据高中知识可以得到这两个向量的内积公式
a∙ b =a1b1+a2b2=‖ a ‖ ‖ b ‖cosa
我们做一个简单的变换
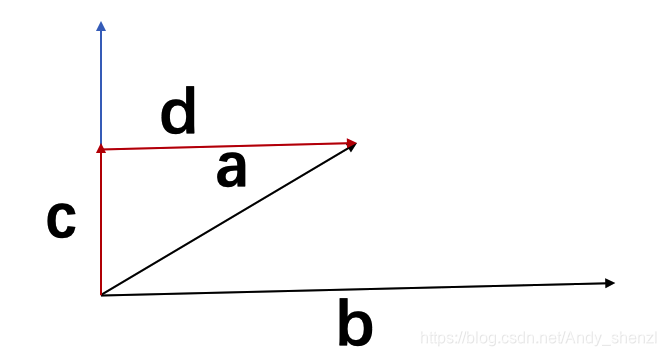
我们再加入两个向量c、 d
a= c + d, c⊥b 且 d//b
那么我们又可以得到
a∙ b
=(c+d) ∙ b
=c∙ b + d ∙ b
= ‖d‖ ‖b‖
这是最基本的公式,接下来会用到
2、平面
超平面的理解
假定W和x是n维向量(vector):
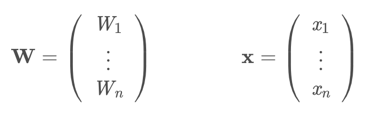
平面方程可以写为:Wx=b或Wx+b=0
二维空间中,满足a1x1 + a2x2 + c = 0 的所有点 (x1, x2) 在几何上是一条直线(类似于 y = k1x + k2)。
三维空间中,满足a1x1 + a2x2 + cx2 = d 的所有点 (x1, x2, x3) 在几何上是空间的一张平面。
n维空间中,满足n元一次方程 a1x1 + a2x2 + … + anxn = b 的所有点 (x1, x2, …, xn) 称为空间的一张超平面(即广义平面)。
点到平面的距离计算
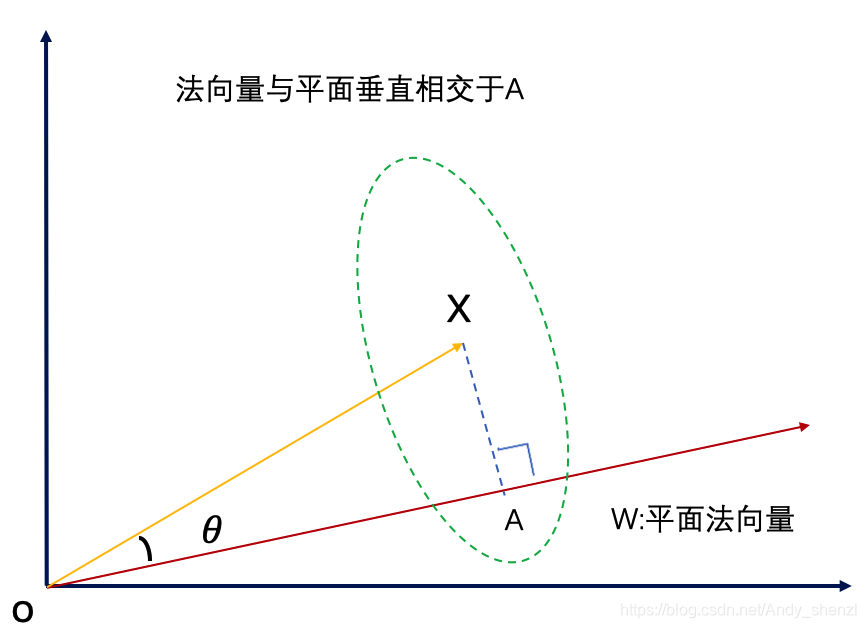
对于:WX=b
这里, W和X表示两个向量, WX即两个向量的内积同时表示向量点集,根据内积公式
 =cosθ ‖x ‖ ‖W ‖
=cosθ ‖x ‖ ‖W ‖
从图中可以看出,cosθ‖ x ‖是向量X 在 W 上的投影(也就是图中 OA = cosθ‖ x ‖ )
也就是说向量点集 WX是 X 在 W 上的投影乘上 W 的长度‖ W ‖ 。
WX = b 的几何意义表示——所有在W上投影长度为 OA的向量集合
进一步我们可以得到
 =OA‖W ‖
=OA‖W ‖

接下来继续
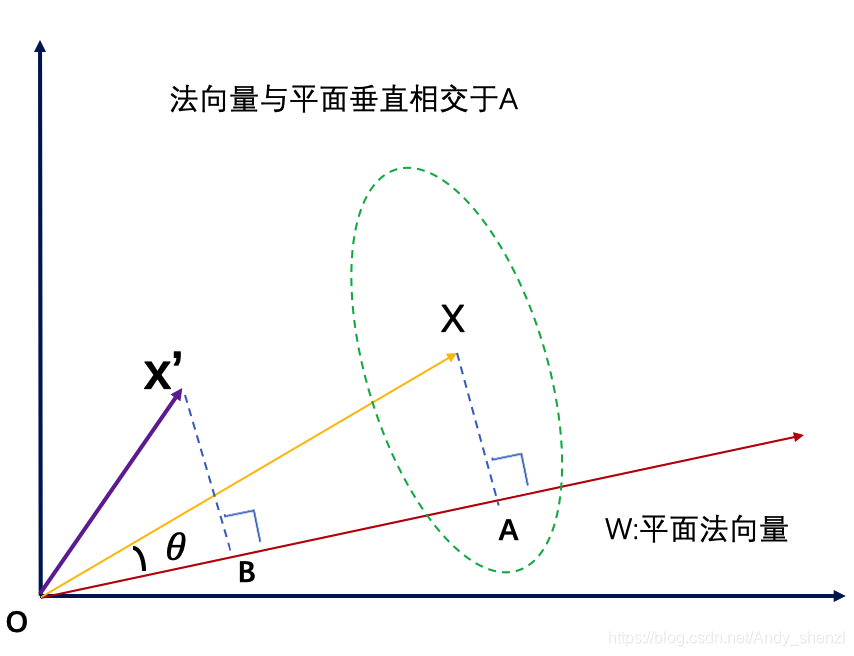
空间中一点x′(也就是向量)到超平面的距离 d
我们做x’到法向量的垂线,相交于B

在SVM的求解中我们就直接引用这个距离公式进行求解
二、拉格朗日乘子法
拉格朗日出生于1736年
这个时期对应的中国,正值清朝,在这前一年雍正去世,爱新觉罗·弘历登基,1736正式改元乾隆
接下来的几十年里形成了鲜明的对比
乾隆皇帝写了4万首诗,并大量搜集诗画在上面盖章,当他在西湖河畔吟着“一片一片又一片,两片三片四五片,六片七片八九片”,苦于无法想出最后一句的时候,浑不知西方的一位数学巨星正在冉冉升起
要理解拉格朗日乘子法,我们要从一个故事入手
the"milkmaid problem”--挤奶女佣问题
在很久很久以前,在农场挤奶的时候,有一个挤牛奶的女仆被送到田间获取当天的牛奶。她很想和一个英俊的年轻牧羊男子约会,所以她想尽快完成工作。但是,在收集牛奶之前,她必须冲洗附近河流中的水桶。
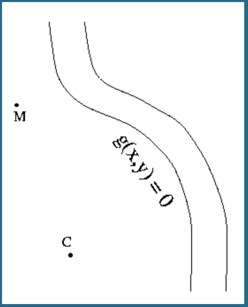
当她到达M点时,我们的女主角发现了那头母牛,需要一直走到C点。因为赶时间,她想走一条尽可能短的路,从M到河再到牛。那么,河岸上冲洗水桶的最佳点P是什么?(为简单起见,我们假定场是平坦且均匀的,并且河岸上的所有点都一样好。)
假设:
河流曲线满足方程 g(x,y) = 0 用P表示河边上的任意P(x,y)点,
用d(M,P)表示M,P之间距离,
那么问题可以描述为:
min f(P) = d(M,P) + d(P,C), 约束条件g(P)= 0
灵感
在高中我们学习过椭圆方程,椭圆方程有一个特性,就是椭圆上任意一点到两个焦点的距离是相等的我们在看这个问题,我们要求MP+CP的最小值,我们可以画出以M和C两点为焦点的椭圆方程
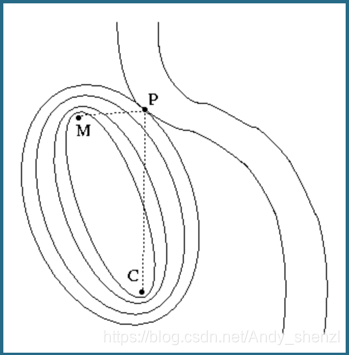
那么椭圆就等于距离的等值线,我们假定椭圆方程f(x,y)
显然,f(x,y)的等值线与河边曲线的交点P即为我们想求的点。
我们需要解决的问题就是: 这样的点满足何种性质?(如果没有性质也就无法列出关系式进行求解,而且这么特殊的点极有可能存在良好某种特性)
最直观的性质:f(x,y)与g(x,y)在P点相切,即等值线(椭圆)在P点的法向量n与河边曲线的法向量m平行:
n =λ m
而在多元微积分中,一个函数f在某一点P的梯度是点P所在等值线(面)
的法向量,即 n =∇𝑓(P),所以对于函数f , g :
![]()
fx= λ gx ----1
fy=λ gy ----2
即由相切点的性质我们得到了2个关系式(因为是二维平面,对于三维则可以得到三个关系式,以此类推)
再加上我们的约束条件:
g(x,y)= 0 ----3
一共3个关系式,由线性代数中知识可知3个关系式,3个未知量(x,y,λ)极有可能有唯一解(如果P在MC所在的直线上,就有无穷个解)
回到我们最初的问题:
minf(P) = d(M,P) + d(P,C)
s.t. g(P) = 0
在多元微积分中如果想求一个函数的极值一般的做法是把∇𝑓(P)=0,如何把这个公式和我们的约束条件∇g(P)=0 统一在一起呢?
试着引入一个λ,定义一个新的函数F(P, λ)= 𝑓(P)-λg(P)
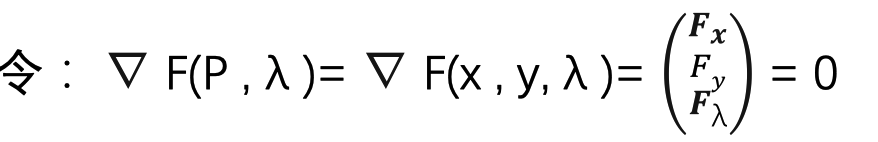
我们可以发现与我们要求解的优化问题是等价的
因为: Fλ=g(P) = g(x, y) = 0 就是前面的约束条件
并且在相切的条件下,F(P , λ)= 𝑓(P)-λ*0=𝑓(P)
即拉格朗日函数 F(P)与我们的目标函数 𝑓(P) 取相同值。用拉格朗日函数把目标函数和约束条件统一在了一起。
到这里我们发现拉格朗日真是天才,看起来很复杂的问题,就这样给解决了

同理可以推导高纬度和多限制条件
三、SVM
接下里要正式进入SVM了
1、线性SVM
通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。
关于SVM,流传着一个关于天使与魔鬼的故事。
传说魔鬼和天使玩了一个游戏,魔鬼在桌上放了两种颜色的球。魔鬼让天使用一根木棍将它们分开。这对天使来说,似乎太容易了。天使不假思索地一摆,便完成了任务。魔鬼又加入了更多的球如下图所示。

SVM实际上是在为天使找到木棒的最佳放置位置,使得两边的球都离分隔它们的木棒足够远。依照SVM为天使选择的木棒位置,魔鬼即使按刚才的方式继续加入新球,木棒也能很好地将两类不同的球分开。
看到这个问题大家很容易想到感知机算法,但是感知机有两个致命的缺点:
第一,区分两类点的直线或者超平面不唯一,而且很难求得最优解(取决于初始参数);
第二,不能解决线性不可分的问题。
什么是最优解呢?如下图
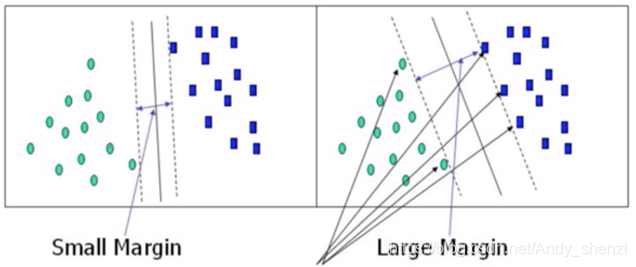
两个分类器都完全正确的区分了两类点,但是我们看到右边的直线分类的效果直觉上要比左边的好。
右边所有的样本不光可以被超平面分开,还和超平面保持一定的函数距离,那么这样的分类超平面是比感知机的分类超平面优的。而且可以证明,这样的超平面只有一个。
假设我们找到了最优的超平面,那么我们也可以找到两类点到超平面距离最近的点(当然有可能是一个也可能是多个),如下图所示;
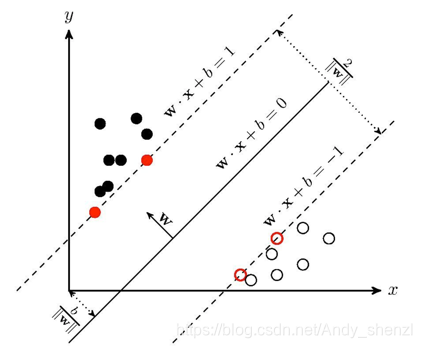

因为距离是正的,所以我们把yi乘到上式,就可以不用考虑正负号问题,去掉绝对值就可以进行化简了
解释:
前面我们为什么把距离平面最近的点距离设为1呢?
答案是为了后面简化方便,那么会不会影响结果呢?
我们来看一下,
比如我们拿离平面最近的正例点xi,那么它距离平面的距离肯定是大于0的,我们可以假定这个距离是γ′
即:Yi=
xi+b=γ′
那么其他的正例点都大于γ′
所以,正例点都满足
xi+b ≥ γ′
两边都比上γ′,
我们可以对比下面两个简单的方程:
x + y = 1
2x + 2y = 2
虽然两个方程的前面的系数不一样,但它们代表相同的直线方程
大家也可以了解下几何间隔与函数间隔的区别
接下来我们优化目标函数
目标:找到距离超平面最近的点,求能使得决策边界最大
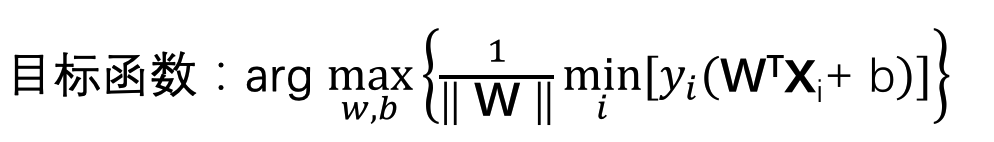
Min里面是指找到最近的点,max是找到最宽的边界
前面我们说了
 xi+b≥ 1
xi+b≥ 1
所以最小值就是1,这样我们就可以把min里面直接拿出来(这就是我们为什么前面把距离假定为1的原因)
也就是我们只需要化简:
![]()
由于我们更习惯于求解最小值,所以我们可以对上面的式子进行等价变换
求解 min 1/2‖W‖2 ,前面加1/2 是为了后面好化简,并不影响结果
这是一个含有不等式约束的凸二次规划问题,可以对其使用拉格朗日乘子法得到其对偶问题
我们将有约束的原始目标函数转换为无约束的新构造的拉格朗日目标函数
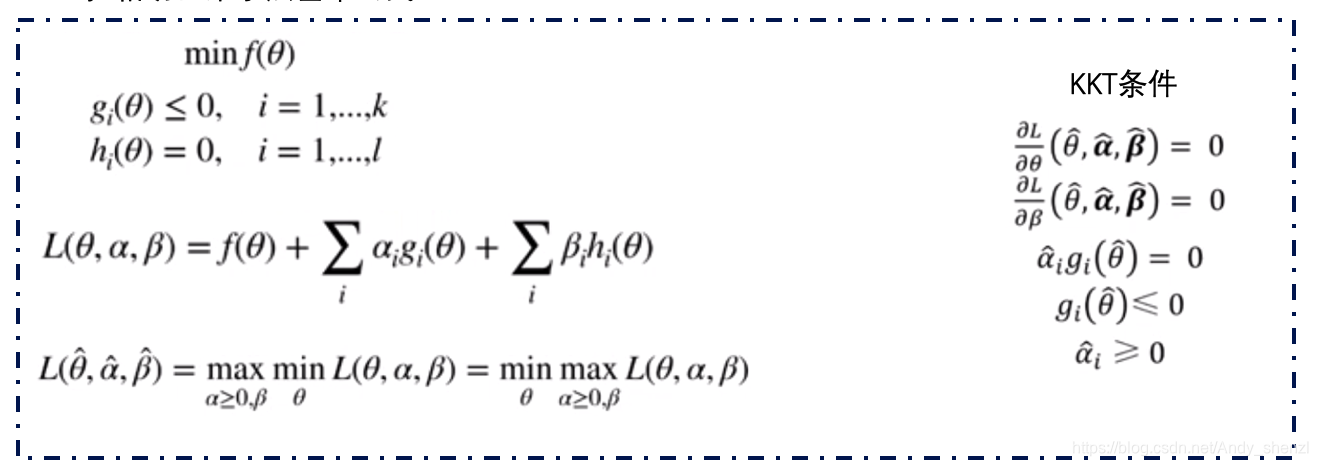

根据KKT条件进行求解:
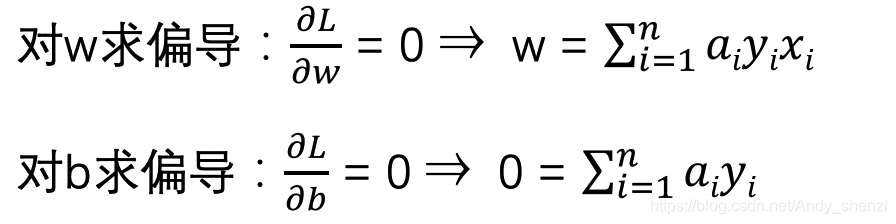
从上两式子可以看出,我们已经求得了w和α的关系,只要我们后面接着能够求出优化函数极大化对应的α,就可以求出我们的w了,至于b,由于上两式已经没有b,而且我们带入后会发现b也会消除掉,我们到后面再说。
下面我们就把w的公式带入带入优化函数L(w,b,α)消去w进行求解α
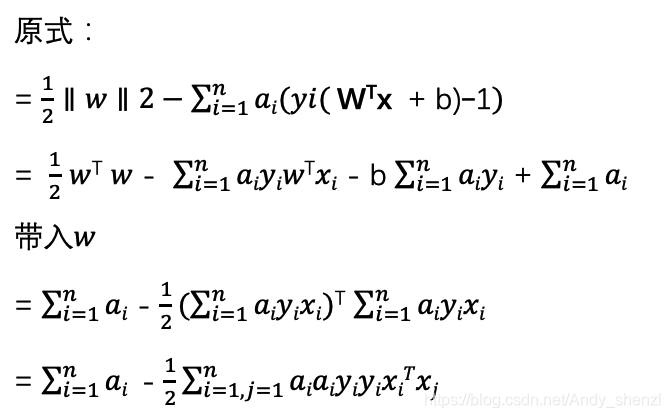
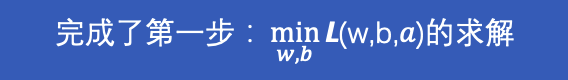
![]()
接下来我们需要求"a"的极大值,根据我们一贯的思维,遇到求极大值,就要想办法转换为求极小值
这里我们只需要加一个负号就可以了
![]()
举例
为了能让大家更好的理解,这里加入一个实例来实际的计算一下
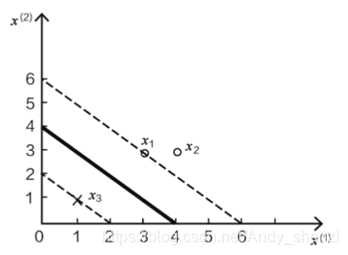
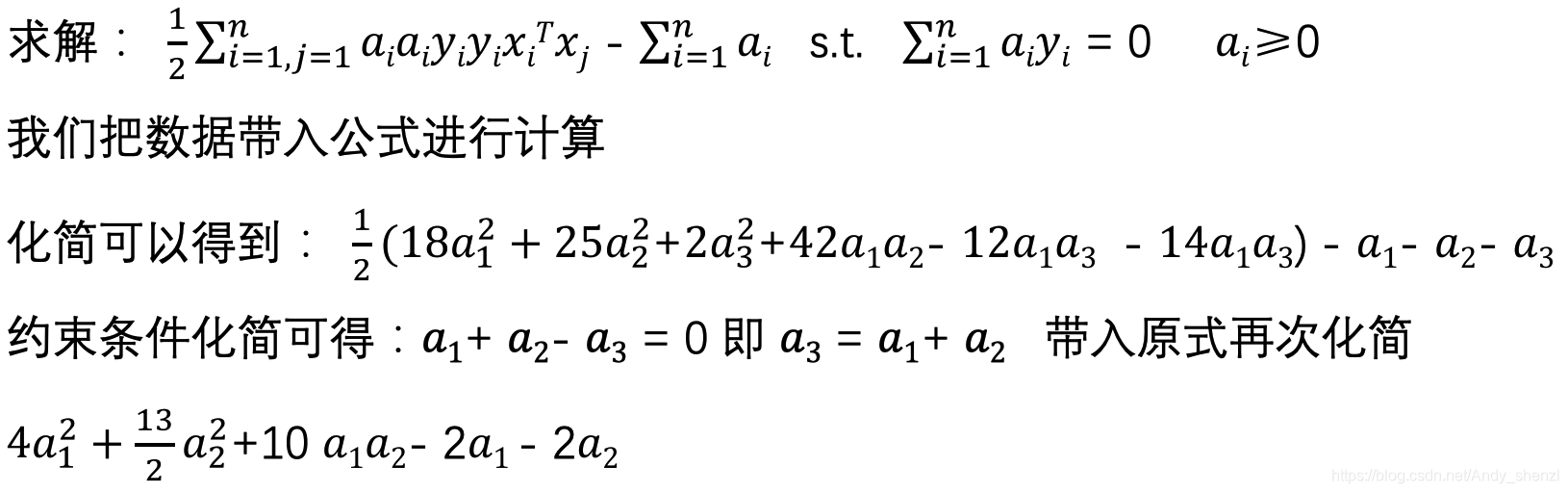
接下来求上式的极小值,即求a1和a2的偏导等于0
![]()
对a1求偏导:8a1+10a2–2=0
对a2求偏导:13a2+10a1–2=0
化简可得:a1=1.5 a2=-1
这里我们发现a2=-1不满足ai ≥0的条件,所以我们需要换一个思维考虑一下
根据条件ai≥0,我们不妨把边界点a1=0或者a2=0 带入进行求解
把a2=0 带入a1求偏导:8a1+10a2–2=0 求得a1=0.25
把a1=0带入a2求偏导:13a2+10a1–2=0求得a2=2/13
带入原式可得当a1=0.25 a2=0 时原式的值最小,同时可以得到a3=0.25
前面我们已经得到了w与a的关系,那么我们带入a,就可以得到w和b
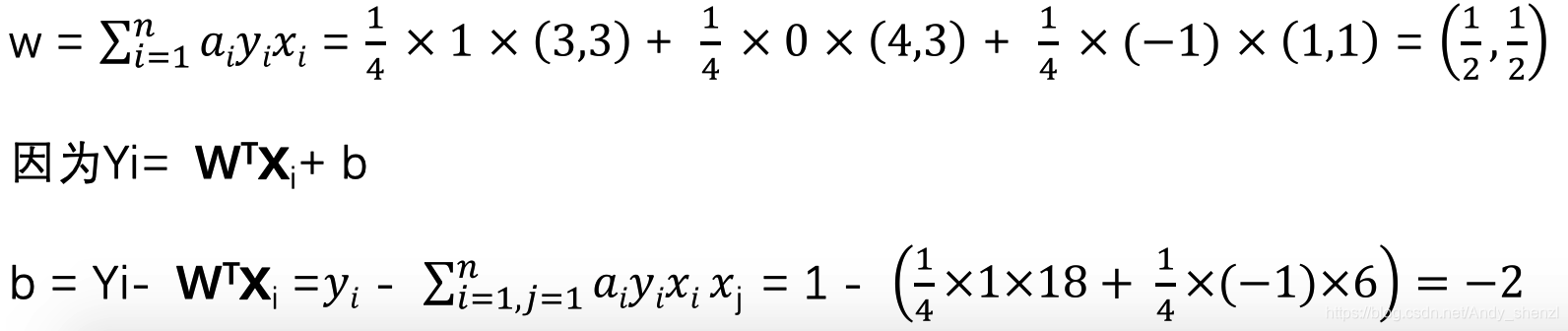
我们把w和b带入方程就可以得到超平面的方程,因为我们计算的是二维所以就是一条直线
即:0.5x1+0.5x2=2
下图中红线即为结果
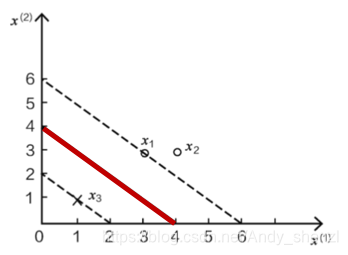
这里我们只有三个样本点,当样本点多的时候我们很难直接带入求解
一般需要用到SMO算法,两两进行求解,这里不进行展开
为什么叫支持向量机?
我们注意到我们求的3个a值中,其中a2=0
同时与a2相关的x,y都没有对结果(w和b)产生影响,
即x2(4, 3)这个点对结果影响的权重为0
只有ai≠ 0时,对应的数据点才会对结果产生作用
(我们也可以证明在经过x1虚线上面和经过x3虚线下面的点都不会对结果产生影响)
而且我们从图上可以看到,x1和x3都是边界上的点,也是距离我们要求的超平面最近的点
我们就把x1和x3这样的点称为支持向量
2、软间隔
如下图:当我们不考虑点A时,可以按照上面的推到得到虚线进行区分
但是当我们加入一个噪声点A时,我们再按照之前的算法进行区分的话,
决策边界就变成了图中的实线,这时可以发现决策边界的宽度窄了很多
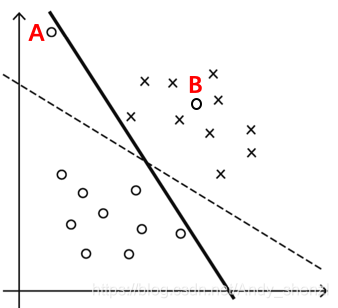
因为我们前面设定了yi˙y(xi) ≥ 0,模型为了满足所有点成立得到了上图的实线
现在我们再加入一个点B,那么现在我们根据之前的假定,就无法得到解
也就是说,我们如果为了满足个别的离群点或者噪音点,反而使得模型过拟合甚至没有解。
所以,为了解决上面的两种情况,可以在一定的程度上降低对模型的要求
引入一个松弛变量或者叫松弛因子𝝃
yi ˙y(xi)=yi( WTx+b)≥1-𝝃
对比硬间隔最大化,可以看到我们对样本到超平面的函数距离的要求放松了,之前是一定要大于等于1,现在只需要加上一个大于等于0的松弛变量能大于等于1就可以了。当然,松弛变量不能白加,这是有成本的,每一个松弛变量ξi,对应了一个代价ξi,这个就得到了我们的软间隔最大化的SVM学习条件如下:
![]()
这里,C>0为惩罚参数,可以理解为我们一般回归和分类问题正则化时候的参数。我们要求上式的最小值,前半部分跟之前一样,但看后边,求最小值的话:
C越大,那么𝝃就必须越小,才能使整体取得极小值,也就是对误分类的惩罚越大,当C趋近于无穷大,那么𝝃趋近于0,则此时求的解就是我们上面求的硬间隔
C越小,那么𝝃的值可以大一点,对误分类的惩罚越小,意味着模型可以有更大的错误容忍度。
那么此时我们的目标函数虽然发生了变化,依然可以根据拉格朗日函数进行转换
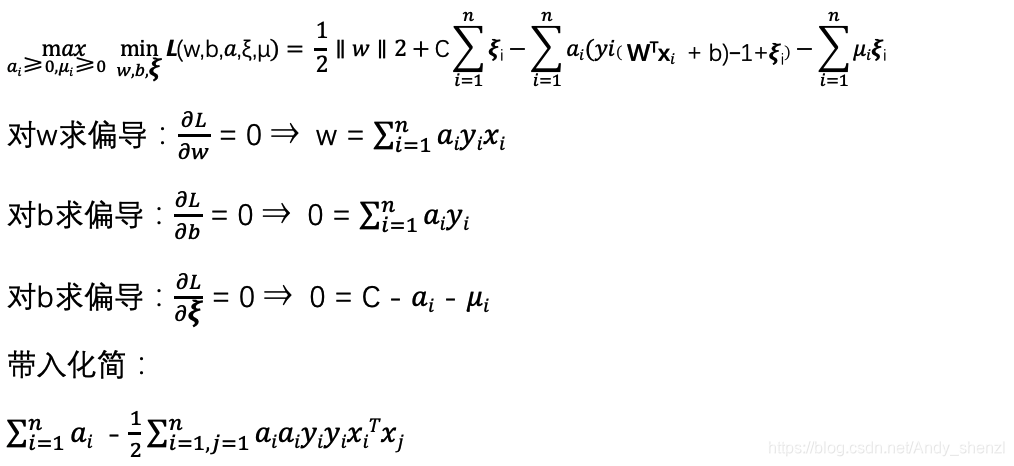
最大值问题转化成求最小值
![]()
3、核函数
再回到我们SVM最开始的位置,恶魔与天使的游戏续:
看到天使已经很好地解决了用木棒线性分球的问题,魔鬼又给了天使新的挑战,如下图所示。

我们发现随着球的增多,以及无规则的摆放越来越不好分了,世界上貌似没有一根木棒可以将它们完美分开。但天使毕竟有法力,他一拍桌子,便让这些球飞到了空中,然后凭借念力抓起一张纸片,插在了两类球的中间。
后来,“无聊”的科学家们把这些球称为“数据”,把木棍称为“分类面”,找到最大间隔的木棒位置的过程称为“优化”,拍桌子让球飞到空中的念力叫“核映射”,在空中分隔球的纸片称为“分类超平面”。这便是SVM的童话故事。
故事讲完了,接下里需要我们想办法学习“法力”了
这个法力就是接下里要讲的就是核函数
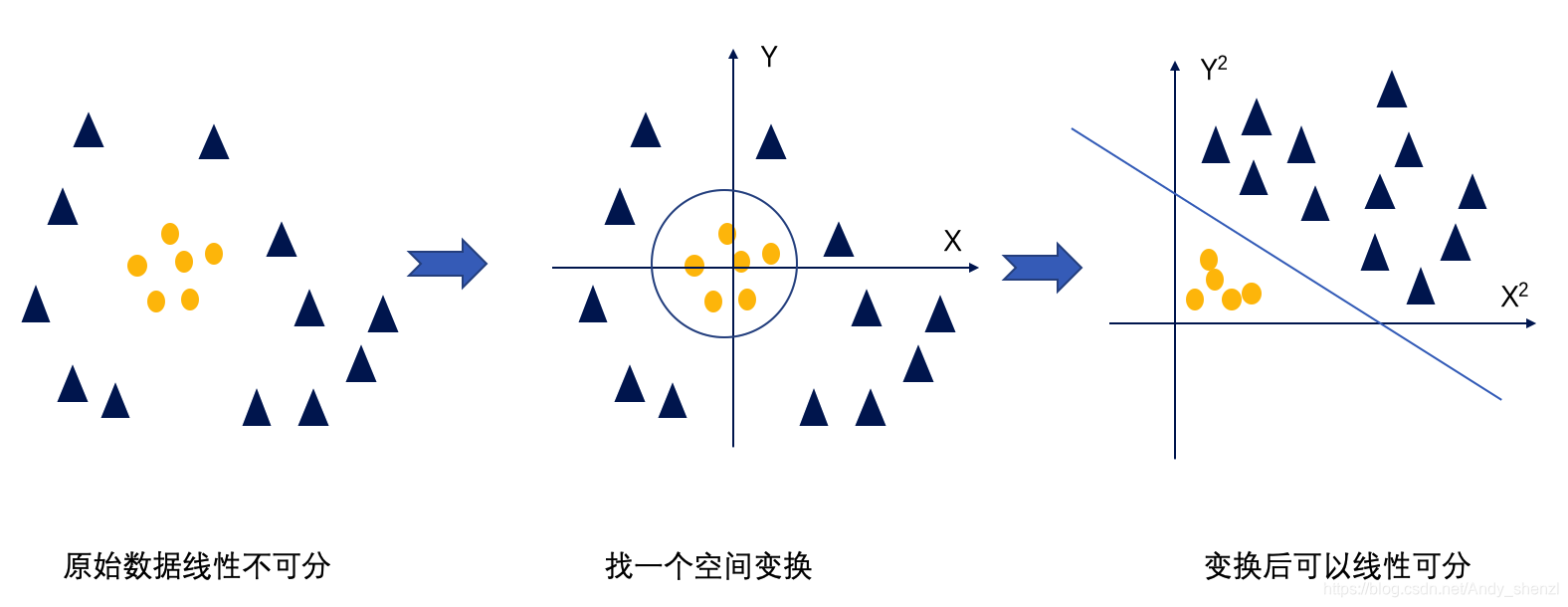
这里会有两个问题,一个是变换函数很难定义(上面的是比较简单的),其次运算复杂度会增大(一般要升维)
核函数就是为了解决这样的问题
假设ϕ是一个从低维的输入空间χ(欧式空间的子集或者离散集合)到高维的希尔伯特空间的H映射。那么如果存在函数K(x,z),对于任意x,z∈χ,都有:
K(x,z)=ϕ(x)∙ϕ(z)
那么我们就称K(x,z)为核函数。
简单举个例子:

核函数简单来说就是只需要在低维空间进行计算,再把结果映射到高维
虽然通过核函数进行了空间变换得到了更多的特征信息,但是计算复杂度没有发生根本变化。
在我们日常使用中,比较常见的核函数:
线性核函数,即我们前面讲的线性可分的情况,可以使用线性核函数;
其次用的比较多的就是高斯核函数,在SVM中也称为径向基核函数(RadialBasis Function,RBF),它是非线性分类SVM最主流的核函数。libsvm默认的核函数就是它。
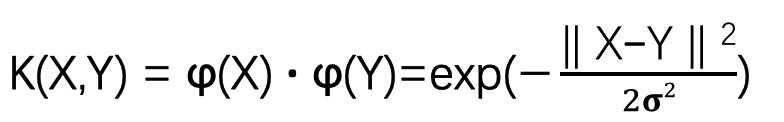
对于高斯核函数,其本身数学内容比较复杂,不展开说明。
直白的理解就是,对于原始数据,先计算两两样本之间的相似度,让其用距离的度量表述数据特征。如果相似结果为1,不相似结果为0。如果进行泰勒展开,可以映射到无限维度。
通过下图来看下,不同核函数是怎么进行分类的
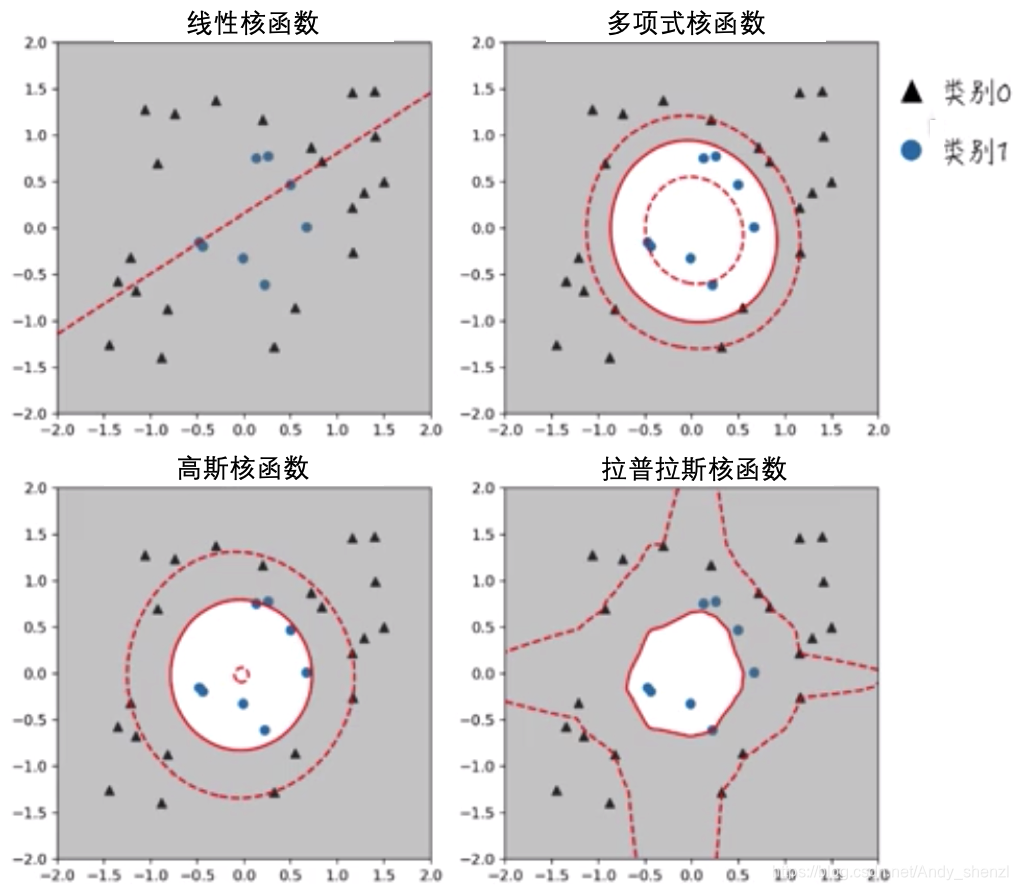
四、python实战
1、线性可分
我们调用iris数据集进行演示
from sklearn import datasets
iris = datasets.load_iris()
X = iris['data'][:,(2,3)]
y = iris['target']
#取其中两种分类
select = (y==0)|(y==1)
X = X[select]
y = list(y[select])
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.plot(X[:,0][y==1],X[:,1][y==1],'bs' ,marker="o")
plt.plot(X[:,0][y==0],X[:,1][y==0],'rs', marker="^")
数据如下
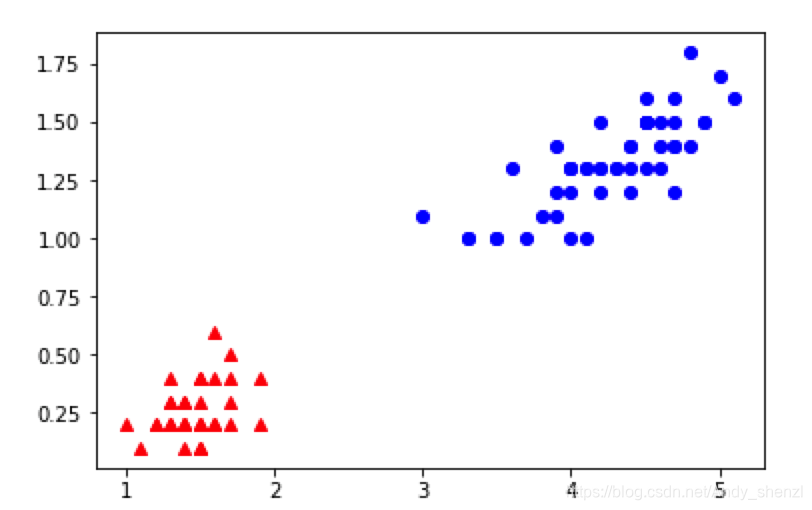
直接调取sklearn中SVC进行分类
from sklearn.svm import SVC
svm_clf = SVC(kernel='linear',C=float('inf'))
svm_clf.fit(X,y)
w = svm_clf.coef_[0]
b = svm_clf.intercept_[0]
x0 = np.linspace(0, 5.5, 200)
decision_boundary = - w[0]/w[1] * x0 - b/w[1]
margin = 1/w[1]
gutter_up = decision_boundary + margin
gutter_down = decision_boundary - margin
plt.plot(X[:,0][y==1],X[:,1][y==1],'bs' ,marker="o")
plt.plot(X[:,0][y==0],X[:,1][y==0],'rs', marker="^")
plt.plot(x0,decision_boundary,'k-',linewidth=2)
plt.plot(x0,gutter_up,'k--',linewidth=2)
plt.plot(x0,gutter_down,'k--',linewidth=2)
svs = svm_clf.support_vectors_
plt.scatter(svs[:,0],svs[:,1],s=180,facecolors='#FFAAAA')
plt.axis([0,5.5,0,2])
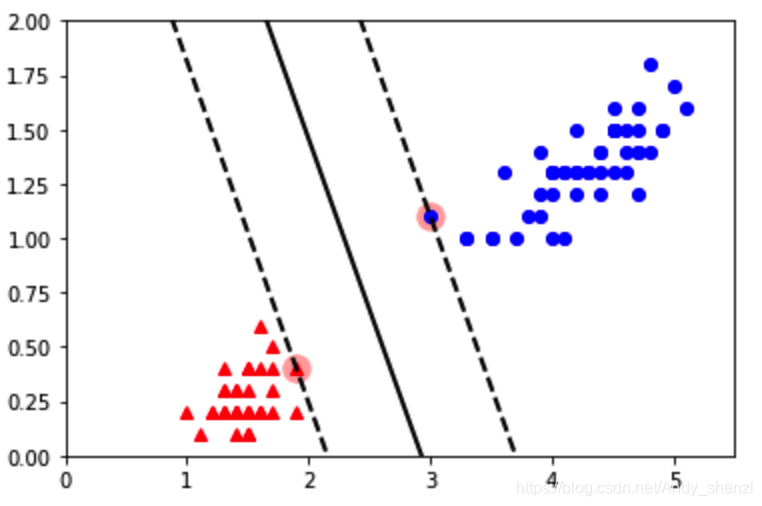
2、软间隔
加入一个噪声点
y= [[0]] * 50 + [[1]] * 50
data = np.concatenate((y, X), axis=1)
data = pd.DataFrame(data, columns=["y", "x1", "x2"])
hardMargin = [[0,2.5, 1.25]]
hardMargin = pd.DataFrame(hardMargin, columns=["y", "x1", "x2"])
data = data.append(hardMargin)
plt.plot(data[data["y"]==0]["x1"],data[data["y"]==0]["x2"],'bs' ,marker="o")
plt.plot(data[data["y"]==1]["x1"],data[data["y"]==1]["x2"],'rs', marker="^")
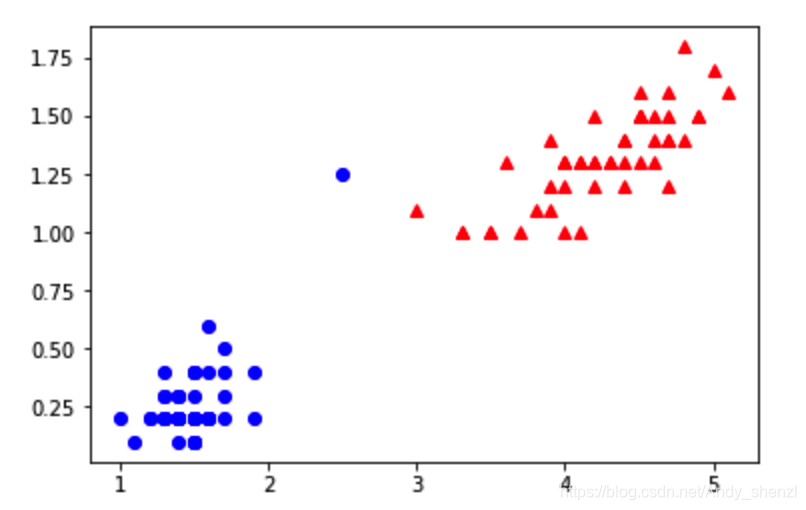
再进行分类
from sklearn.svm import SVC
svm_clf = SVC(kernel='linear',C=float('inf'))
svm_clf.fit(data[["x1", "x2"]], data["y"])
w = svm_clf.coef_[0]
b = svm_clf.intercept_[0]
print (w)
x0 = np.linspace(0, 5.5, 200)
decision_boundary = - w[0]/w[1] * x0 - b/w[1]
margin = 1/w[1]
gutter_up = decision_boundary + margin
gutter_down = decision_boundary - margin
plt.plot(data[data["y"]==0]["x1"],data[data["y"]==0]["x2"],'bs' ,marker="o")
plt.plot(data[data["y"]==1]["x1"],data[data["y"]==1]["x2"],'rs', marker="^")
plt.plot(x0,decision_boundary,'k-',linewidth=2)
plt.plot(x0,gutter_up,'k--',linewidth=2)
plt.plot(x0,gutter_down,'k--',linewidth=2)
svs = svm_clf.support_vectors_
plt.scatter(svs[:,0],svs[:,1],s=180,facecolors='#FFAAAA')
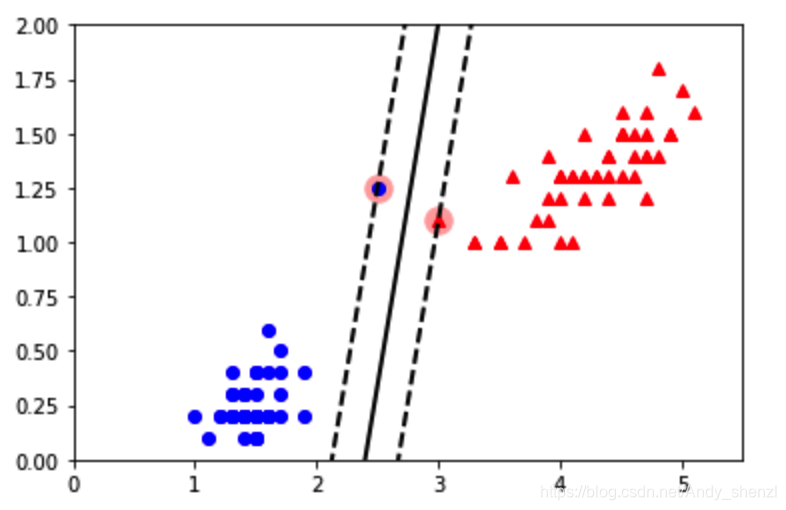
可以看到间隔明显小了很多
我们引入松弛因子,即调整参数C
from sklearn.svm import SVC
svm_clf = SVC(kernel='linear',C=1)
svm_clf.fit(data[["x1", "x2"]], data["y"])
w = svm_clf.coef_[0]
b = svm_clf.intercept_[0]
print (w)
x0 = np.linspace(0, 5.5, 200)
decision_boundary = - w[0]/w[1] * x0 - b/w[1]
margin = 1/w[1]
gutter_up = decision_boundary + margin
gutter_down = decision_boundary - margin
plt.plot(data[data["y"]==0]["x1"],data[data["y"]==0]["x2"],'bs' ,marker="o")
plt.plot(data[data["y"]==1]["x1"],data[data["y"]==1]["x2"],'rs', marker="^")
plt.plot(x0,decision_boundary,'k-',linewidth=2)
plt.plot(x0,gutter_up,'k--',linewidth=2)
plt.plot(x0,gutter_down,'k--',linewidth=2)
svs = svm_clf.support_vectors_
plt.scatter(svs[:,0],svs[:,1],s=180,facecolors='#FFAAAA')
plt.axis([0,5.5,0,2])
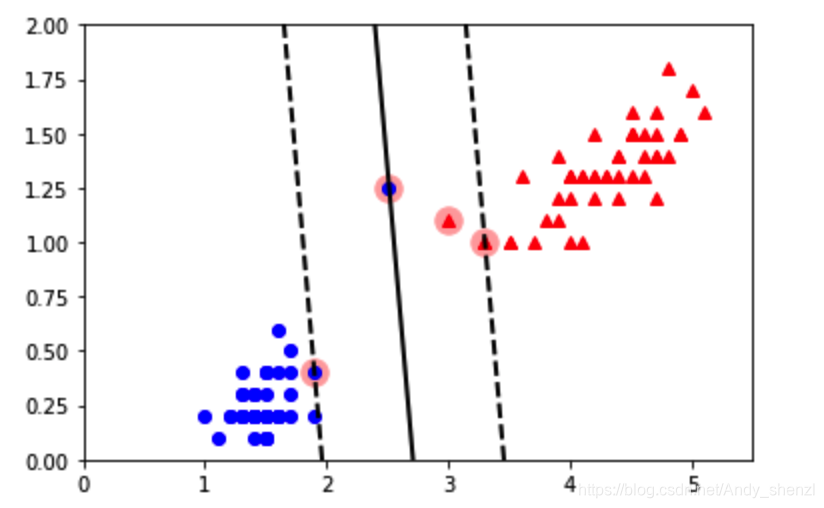
我们发现,排除了噪声点,间隔变大
3、核函数
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)
plt.plot(X[:, 0][y==0], X[:, 1][y==0] ,'bs' ,marker="o")
plt.plot(X[:, 0][y==1], X[:, 1][y==1],'rs', marker="^")
plt.axis([-1.5, 2.5, -1, 1.5])
plt.grid(True, which='both')
plt.show()
rbf= SVC(kernel='rbf', gamma=1)
rbf.fit(X,y)
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)
plt.plot(X[:, 0][y==0], X[:, 1][y==0] ,'bs' ,marker="o")
plt.plot(X[:, 0][y==1], X[:, 1][y==1],'rs', marker="^")
plt.axis([-1.5, 2.5, -1, 1.5])
plt.grid(True, which='both')
x0s = np.linspace(-1.5,2.5,100)
x1s = np.linspace(-1,1.5,100)
x0,x1 = np.meshgrid(x0s,x1s)
X = np.c_[x0.ravel(),x1.ravel()]
y_pred = rbf.predict(X).reshape(x0.shape)
plt.contourf(x0,x1,y_pred,cmap=plt.cm.brg,alpha=0.2)
五、总结:
1、SVM就是要找到一个超平面把两类点进行最优分类;
2、如果数据中有噪音点,为了避免过拟合需要引入松弛因子进行软间隔分类;
3、对于线性不可分的数据,要引入核函数进行分类。
来源:CSDN
作者:Andy_shenzl
链接:https://blog.csdn.net/Andy_shenzl/article/details/104856607
 xi+b=γ′
xi+b=γ′
 xi+b ≥ γ′
xi+b ≥ γ′
