Khan_Computer Science_Algorithms

1. Intro to algorithms

1.1 What is an algorithm and why should you care?

What is an algorithm? One definition might be a set of steps to accomplish a task. You might have an algorithm for getting from home to school, for making a grilled cheese sandwich, or for finding what you're looking for in a grocery store.

In computer science, an algorithm is a set of steps for a computer program to accomplish a task. Algorithms put the science in computer science. And finding good algorithms and knowing when to apply them will allow you to write interesting and important programs.

Let's talk about a few famous algorithms. How does Google Hangouts transmit live video across the Internet so quickly? They use audio and video compression algorithms.

How does Google Maps figure out how to get from Dallas, Texas to Orlando, Florida so that you can get to Disney World? They use a route finding algorithm.

How does Nasa choose how to arrange the solar panels on the International Space Station and when to rearrange them? They use an optimization and a scheduling algorithm.

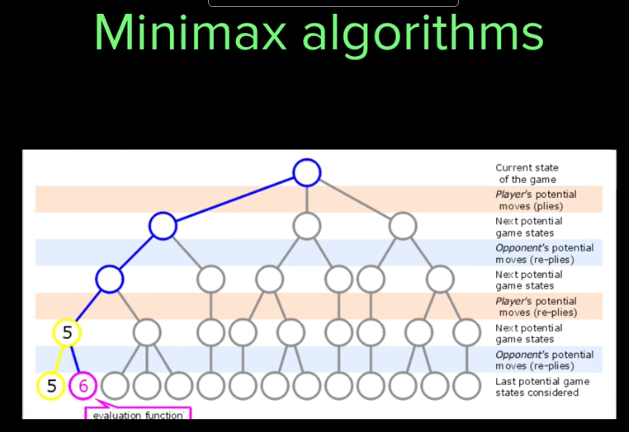
For example, let's say that you're writing a game and you want the user to be able to play against the computer. Well, you could look at checkers games for inspiration. Computer scientists have figured out how to write checkers programs that never lose by using the minimax search algorithm to search through the huge tree of possible moves. If your game is similar to checkers, then you might be able to use algorithms based on these techniques. If not, then knowing the limitations of those algorithms might lead you to redesign your game if it requires having a skilled computer player.

1.2 A guessing game

Let's play a little game to give you an idea of how different algorithms for the same problem can have wildly different efficiencies. The computer is going to randomly select an integer from 1 to 16. You'll keep guessing numbers until you find the computer's number, and the computer will tell you each time if your guess was too high or too low:

Maybe you guessed 1, then 2, then 3, then 4, and so on, until you guessed the right number. We call this approach linear search, because you guess all the numbers as if they were lined up in a row. It would work. But what is the highest number of guesses you could need?

you can start off by guessing 8. If the number that the computer selected is less than 8, then because you know that 8 is too high, you can eliminate all the numbers from 8 to 16 from further consideration. If the number selected by the computer is greater than 8, then you can eliminate 1 through 7. Either way, you can eliminate about half the numbers. On your next guess, eliminate half of the remaining numbers. Keep going, always eliminating half of the remaining numbers. We call this halving approach binary search,

2. Binary search

In order to implement an algorithm in a programming language, you will need to understand an algorithm down to the details. What are the inputs to the problem? The outputs? What variables should be created, and what initial values should they have? What intermediate steps should be taken to compute other values and to ultimately compute the output? Do these steps repeat instructions that can be written in simplified form using a loop?

2.1 Binary Search

Binary search is an efficient algorithm for finding an item from a sorted list of items. It works by repeatedly dividing in half the portion of the list that could contain the item, until you've narrowed down the possible locations to just one.

One of the most common ways to use binary search is to find an item in an array. For example, the Tycho-2 star catalog contains information about the brightest 2,539,913 stars in our galaxy. Suppose that you want to search the catalog for a particular star, based on the star's name. If the program examined every star in the star catalog in order starting with the first, an algorithm called linear search, the computer might have to examine all 2,539,913 stars to find the star you were looking for, in the worst case. If the catalog were sorted alphabetically by star names, binary search would not have to examine more than 22 stars, even in the worst case.

The next few articles discuss how to describe the algorithm carefully, how to implement the algorithm in JavaScript, and how to analyze efficiency.

Describing binary search

When describing an algorithm to a fellow human being, an incomplete description is often good enough. Some details may be left out of a recipe for a cake; the recipe assumes that you know how to open the refrigerator to get the eggs out and that you know how to crack the eggs. People might intuitively know how to fill in the missing details, but computer programs do not. That's why we need to describe computer algorithms completely.

Let's look at how to describe binary search carefully. The main idea of binary search is to keep track of the current range of reasonable guesses. Let's say that I'm thinking of a number between one and 100, just like the guessing game. If you've already guessed 25 and I told you my number was higher, and you've already guessed 81 and I told you my number was lower, then the numbers in the range from 26 to 80 are the only reasonable guesses. Here, the red section of the number line contains the reasonable guesses, and the black section shows the guesses that we've ruled out:

In each turn, you choose a guess that divides the set of reasonable guesses into two ranges of roughly the same size. If your guess is not correct, then I tell you whether it's too high or too low, and you can eliminate about half of the reasonable guesses. For example, if the current range of reasonable guesses is 26 to 80, you would guess the halfway point,

For the guessing game, we can keep track of the set of reasonable guesses using a few variables. Let the variable

Here's a step-by-step description of using binary search to play the guessing game:

Let
Guess the average of
If you guessed the number, stop. You found it!
If the guess was too low, set
If the guess was too high, set
Go back to step two.

We could make that description even more precise by clearly describing the inputs and the outputs for the algorithm and by clarifying what we mean by instructions like "guess a number" and "stop." But this is enough detail for now.

Next up, we'll see how we can use binary search on an array, and discuss how to turn descriptions of algorithms into actual working code.

2.4 Running time of binary search

We know that linear search on an array of

The key idea is that when binary search makes an incorrect guess, the portion of the array that contains reasonable guesses is reduced by at least half. If the reasonable portion had 32 elements, then an incorrect guess cuts it down to have at most 16. Binary search halves the size of the reasonable portion upon every incorrect guess.

If we start with an array of length 8, then incorrect guesses reduce the size of the reasonable portion to 4, then 2, and then 1. Once the reasonable portion contains just one element, no further guesses occur; the guess for the 1-element portion is either correct or incorrect, and we're done. So with an array of length 8, binary search needs at most four guesses.

What do you think would happen with an array of 16 elements? If you said that the first guess would eliminate at least 8 elements, so that at most 8 remain, you're getting the picture. So with 16 elements, we need at most five guesses.

By now, you're probably seeing the pattern. Every time we double the size of the array, we need at most one more guess. Suppose we need at most

Let's look at the general case of an array of length

Fortunately, there's a mathematical function that means the same thing as the number of times we repeatedly halve, starting at

\log2​n, but you may also see it written as \lg nlgn in computer science writings. (Want to review logarithms? Learn more here.)

Here's a table showing the base-2 logarithms of various values of

We can view this same table as a graph:

Zooming in on smaller values of n:

The logarithm function grows very slowly. Logarithms are the inverse of exponentials, which grow very rapidly, so that if

\log_2 n = xlog2​n=x, then n = 2^xn=2x. For example, because \log_2 128 = 7log2​128=7, we know that 2^7 = 12827=128.

That makes it easy to calculate the runtime of a binary search algorithm on an

(\log_2 128 + 1log2​128+1) guesses.

What if

2^{9}29. We can thus estimate that \log_2 1000log2​1000 is a number greater than 9 and less than 10, or use a calculator to see that its about 9.97. Adding one to that yields about 10.97. In the case of a decimal number, we round down to find the actual number of guesses. Therefore, for a 1000-element array, binary search would require at most 10 guesses.

For the Tycho-2 star catalog with 2,539,913 stars, the closest lower power of 2 is

2^{21}221 (which is 2,097,152), so we would need at most 22 guesses. Much better than linear search!

Compare

\log _{2} nlog2​n below:

In the next tutorial, we'll see how computer scientists characterize the running times of linear search and binary search, using a notation that distills the most important part of the running time and discards the less important parts.

3. Asymptotic notation

3.1 Asymptotic notation

4. Selection sort

5. Insertion sort

6. Recursive algorithms

7. Towers of Hanoi

8. Merge sort

9. Quick sort

10. Graph representation

11. Breadth-first search

12. Further learning