贝叶斯分类器中的涉及到的数学知识基本上是概率论与数理统计，其计算步骤倒是不难，西瓜书上的公式表示可能让人没有看下去的欲望，博主最开始学的时候也就是直接拿个例子计算一遍，然后再去看看西瓜书上的公式。贝叶斯中的核心计算公式就是条件概率的计算公式。
先看看条件概率的计算公式：
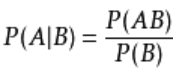
上面这个公式指的是事件A在事件B发生的条件下发生的概率。同理：P(B|A) = P(AB)/P(A)。这样上面也可以写成
。
接下来，我们直接看个例子，以西瓜书上的例子来看：
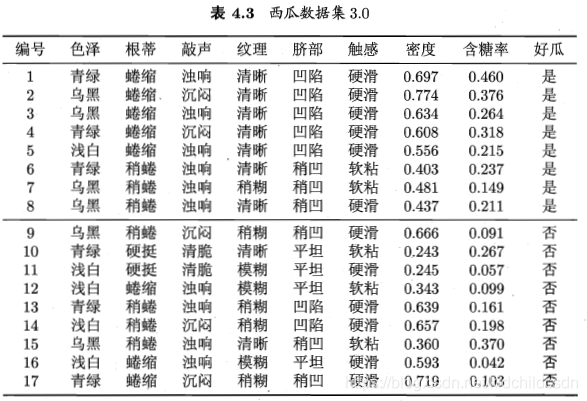
使用以上数据集作为训练集来训练贝叶斯分类器。 现在来了一个新的数据：
根据新样本的属性值，我们需要判断这个样本是好瓜的概率有多大。很明显我们需要计算：P(好瓜 | 色泽=青绿，根蒂=蜷缩，敲声=浊响，纹理=清晰，脐部=凹陷，密度=0.697，含糖率=0.460)，这些属性值的条件下，好瓜的概率。将条件概率的公式代入：P(好瓜 | 色泽=青绿，根蒂=蜷缩，敲声=浊响，纹理=清晰，脐部=凹陷，密度=0.697，含糖率=0.460) =
P(色泽=青绿，根蒂=蜷缩，敲声=浊响，纹理=清晰，脐部=凹陷，密度=0.697，含糖率=0.460，好瓜) / P(色泽=青绿，根蒂=蜷缩，敲声=浊响，纹理=清晰，脐部=凹陷，密度=0.697，含糖率=0.460) =
P(好瓜) X P(色泽=青绿，根蒂=蜷缩，敲声=浊响，纹理=清晰，脐部=凹陷，密度=0.697，含糖率=0.460 | 好瓜) / P(色泽=青绿，根蒂=蜷缩，敲声=浊响，纹理=清晰，脐部=凹陷，密度=0.697，含糖率=0.460)。
所以我们需要计算P(好瓜) 、P(色泽=青绿，根蒂=蜷缩，敲声=浊响，纹理=清晰，脐部=凹陷，密度=0.697，含糖率=0.460 | 好瓜)、P(色泽=青绿，根蒂=蜷缩，敲声=浊响，纹理=清晰，脐部=凹陷，密度=0.697，含糖率=0.460)，这些如何计算？？？ 从我们的训练集中计算。
从训练集中统计数据，很明显，P(好瓜) = 8/17。我们这里有个前提是假设属性条件独立，意味着每个属性对分类结果产生的影响互不相关，这样使得我们的计算更加方便。有了这个前提：
P(色泽=青绿，根蒂=蜷缩，敲声=浊响，纹理=清晰，脐部=凹陷，密度=0.697，含糖率=0.460 | 好瓜) = P(色泽=青绿 | 好瓜) X P(根蒂=蜷缩 | 好瓜) X P(敲声=浊响 | 好瓜) X P(纹理=清晰 | 好瓜) X P(脐部=凹陷 | 好瓜) X P(密度=0.697 | 好瓜) X P(含糖率=0.460 | 好瓜)
P(色泽=青绿 | 好瓜) 就是在好瓜的前提下，色泽是青绿的概率，我们可以从训练集中看出，有8个是好瓜，其中色泽青绿的有3个，所以P(色泽=青绿 | 好瓜) = 3/8，同理，P(根蒂=蜷缩 | 好瓜) 、 P(敲声=浊响 | 好瓜) 、 P(纹理=清晰 | 好瓜) 、 P(脐部=凹陷 | 好瓜)这些都可以算出来。然而，P(密度=0.697 | 好瓜) 和 P(含糖率=0.460 | 好瓜) 涉及到了连续属性，就不单单是简单的像离散属性那样统计个数那么简单。所以引入了高斯分布，其大意就是，在同一类别中，连续属性的属性值符合某一正态分布：
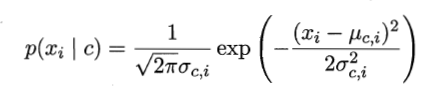
其中c是类别，
是连续属性，剩下的就是计算均值和方差，只要有训练集，计算均值和方差不难。 根据上面的公式可以计算P(密度=0.697 | 好瓜) 和 P(含糖率=0.460 | 好瓜)：
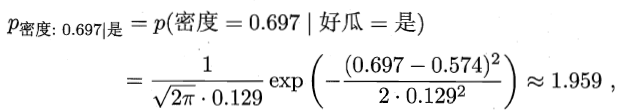
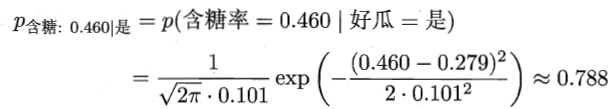
如此一来，就只剩下P(色泽=青绿，根蒂=蜷缩，敲声=浊响，纹理=清晰，脐部=凹陷，密度=0.697，含糖率=0.460)需要计算，因为其中的属性条件独立，所以P(色泽=青绿) = P(根蒂=蜷缩) X P(敲声=浊响) X P(纹理=清晰) X P(脐部=凹陷) X P(密度=0.697) X P(含糖率=0.460) 。这些都可以从训练集中计算出来，离散属性统计个数计算就行，如P(根蒂=蜷缩) = 8/17,17个样本中只有8个样本的根蒂是蜷缩的，同理，其他的离散属性的概率值均可计算出。对于P(密度=0.697)和P(含糖率=0.460)来说，需要借助上面引入的正态分布函数，这个时候就是计算整个训练集中的平均值和均值，代入上面的正态分布函数中，而不是仅仅计算某一类别的。
通过上面这个例子，可以知道贝叶斯分类器的大致工作原理。
来源：CSDN
作者：Lavender-csdn
链接：https://blog.csdn.net/kidchildcsdn/article/details/104798859