机器学习-线性回归

机器学习-线性回归算法简单理解

一、基本含义

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为y = w’x+e，e为误差服从均值为0的正态分布。
回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

二、拟合方程

我们所采用的拟合方程为最小二乘法，可以计算出对于y=bx+a的直线。
可以计算出对于y=bx+a的直线。同时可以表示为y = x.T*w , x = [x0 x1].T , w = [b w].T;

三、损失函数

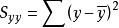
其原理为真实值与预测值的差值

实现过程

一、导入相关模块

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import random

二、生成数据集

x,y= [],[]
for i in range(1,100):
    x.append([1,2*(i+random.uniform(-0.3,0.3))+3+random.random()])
    y.append([i+random.uniform(-5,5)])
x = np.matrix(x)
y = np.matrix(y)

三、可视化数据，观察变化特性

plt.scatter(y.A,x[:,1].A,c='b',s=5)
plt.show()

四、计算参数矩阵

xtx = x.T*x;
if(np.linalg.det(xtx)==0): #判断行列式是否等于0，如果等于0则不可逆，求伪逆
	ws = np.linalg.pinv(xtx) * (x.T*y)
else ws = xtx.I * (x.T*y)

其中依据的数学公式为：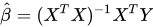

五、绘制结果图像

yhat = x*ws;#计算预测的y值
plt.scatter(x[:,1].A,y.A,c='b',s=5)
plt.plot(x[:,1],yhat,"r")
plt.show()

通过观察图像，拟合效果还是相当不错的。但是对于大多数模型，还需要细化和修改。

局部加权线性回归：https://editor.csdn.net/md?articleId=104757030

来源：CSDN

作者：xavier_zw

链接：https://blog.csdn.net/xavieraa/article/details/104756013