罗德里格斯旋转方程是从角度和向量计算出相应的旋转矩阵,这个旋转方程在很多方面有重要的应用,这里简要概述一下方程的推导过程。
主要参考资料是维基百科,其实基本上就是翻译一下,自己走一遍这个推导过程,这里把链接贴出来。
推导过程:
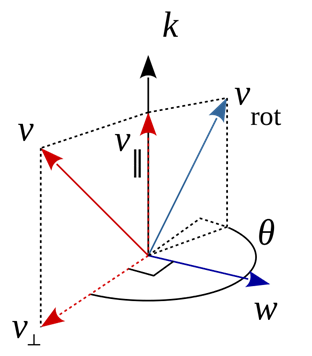
整个推导过程都是围绕上面的图片开展的,进行向量推导。
首先,定义向量k是旋转轴的单位矢量,向量v是绕向量k旋转角度θ的任意向量(旋转方向遵循右手定则,图中逆时针)。
使用点乘和叉乘,向量v可以分解成与轴k平行和垂直的分量,
$\mathbf{v}=\mathbf{v}_{\parallel}+\mathbf{v}_{\bot}$ (1-1)
与k平行的分量是
$\mathbf{v}_{\parallel}=\left( \mathbf{v}\cdot \mathbf{k} \right) \mathbf{k}$ (1-2)
向量v在k上的向量投影,垂直于k的分量为
$\mathbf{v}_{\bot}=\mathbf{v}-\mathbf{v}_{\parallel}=\mathbf{v}-\left( \mathbf{k}\cdot \mathbf{v} \right) \mathbf{k}=-\mathbf{k}\times \left( \mathbf{k}\times \mathbf{v} \right) $ (1-3)
矢量$\mathbf{k}\times \mathbf{v}$可以看作是$\mathbf{v}_{\bot}$绕k逆时针旋转90°的副本,所以它们的大小相等,但是方向是垂直的。同样,向量 $\mathbf{k}\times \left( \mathbf{k}\times \mathbf{v} \right) $是$\mathbf{v}_{\bot}$绕k逆时针旋转180°的副本,使得$\mathbf{k}\times \left( \mathbf{k}\times \mathbf{v} \right) $和$\mathbf{v}_{\bot}$的大小相等,但方向相反(因此符号相反)。
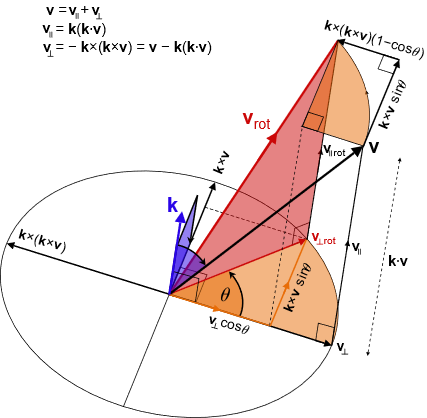
平行于轴的分量在旋转时不会改变幅度和方向:
$\mathbf{v}_{\parallel rot}=\mathbf{v}_{\parallel}$ (1-4)
根据以上分析,垂直分量在旋转时会改变方向,但保持其大小:
$\left| \left. \mathbf{v}_{\bot \text{rot}} \right| \right. =\left| \left. \mathbf{v}_{\bot} \right| \right. $ (1-5)
并且由于k和$\mathbf{v}_{\parallel}$是平行的,所以它们的叉积是零 k×$\mathbf{v}_{\parallel}$ = 0,因此
$\mathbf{k}\times \mathbf{v}_{\bot}=\mathbf{k}\times \left( \mathbf{v}-\mathbf{v}_{\parallel} \right) =\mathbf{k}\times \mathbf{v}-\mathbf{k}\times \mathbf{v}_{\parallel}=\mathbf{k}\times \mathbf{v}\\\mathbf{v}_{\parallel \text{rot}}=\mathbf{v}_{\parallel}$ (1-6)
因此
$\mathbf{v}_{\bot \text{rot}}=\cos \theta \,\,\mathbf{v}_{\bot}+\sin \theta \,\,\mathbf{k}\times \mathbf{v}_{\bot}$ (1-7)
这种旋转是正确的,因为矢量$\mathbf{v}_{\bot}$和k×v具有相同的长度,并且k×v是$\mathbf{v}_{\bot}$围绕k逆时针旋转90°。使用三角函数正弦和余弦对v⊥和k×v进行适当乘积可以得到旋转的垂直分量。旋转分量的形式类似于笛卡尔基的2D平面极坐标(r,θ)中的径向向量
$\mathbf{r}=r\cos \theta \boldsymbol{e}_x+r\sin \theta \boldsymbol{e}_y$ (1-8)
其中$\boldsymbol{e}_x$,$\boldsymbol{e}_y$是它们指示方向上的单位向量。
现在完整的旋转矢量
![]() (1-9)
(1-9)
用上述结果中的和的定义代替
 (1-10)
(1-10)
矩阵表示上式,将v和k×v表示为列矩阵,叉积可以表示为矩阵乘积。
已知,对于两个向量,a, b有:
$\boldsymbol{a}=\left( x_1,y_1,z_1 \right) \\\boldsymbol{b}=\left( x_2,y_2,z_2 \right) \\\boldsymbol{a}\times \boldsymbol{b}=\left| \begin{matrix} \boldsymbol{i}& \boldsymbol{j}& \boldsymbol{k}\\ x_1& y_1& z_1\\ x_2& y_2& z_2\\\end{matrix} \right|=\left( y_1z_2-y_2z_1 \right) \boldsymbol{i}+\left( x_1z_2-x_2z_1 \right) \boldsymbol{j}+\left( x_1y_2-x_2y_1 \right) \boldsymbol{k}$
则的(1-10)可以用矩阵表示为:
$\left[ \begin{array}{c} \left( \mathbf{k}\times \mathbf{v} \right) _x\\ \left( \mathbf{k}\times \mathbf{v} \right) _y\\ \left( \mathbf{k}\times \mathbf{v} \right) _z\\\end{array} \right] =\left[ \begin{array}{c} k_yv_z-k_zv_y\\ k_zv_x-k_xv_z\\ k_xv_y-k_yv_x\\\end{array} \right] =\left[ \begin{matrix} 0& -k_z& k_y\\ k_z& 0& -k_x\\ -k_y& k_x& 0\\\end{matrix} \right] \left[ \begin{array}{c} v_x\\ v_y\\ v_z\\\end{array} \right] $ (1-11)
令矩阵K表示单位向量k的“反对称矩阵"(有时被称作为叉积矩阵):
$\mathbf{K}=\left[ \begin{matrix} 0& -k_z& k_y\\ k_z& 0& -k_x\\ -k_y& k_x& 0\\\end{matrix} \right] =\mathbf{k}^{\land}$ (1-12)
矩阵方程可以表示为
$\mathbf{Kv}=\mathbf{k}\times \mathbf{v}\,\,=\,\,\mathbf{k}^{\land}\mathbf{v}$ (1-13)
对于任何向量v(实际上,矩阵K是具有特征值0和±i)。
迭代右边的叉乘,相当于乘以左边的反对称矩阵,如下
$\mathbf{KKv}=\mathbf{K}^2\mathbf{v}=\mathbf{k}\times \left( \mathbf{k}\times \mathbf{v} \right) \,\,=\mathbf{k}^{\land}\mathbf{k}^{\land}\mathbf{v}$ (1-14)
而且,由于k是单位向量,所以k具有单位2-范数。 因此旋转公式(1-10)可以表示为
$\mathbf{v}_{\text{rot}}=\mathbf{v}+\sin \theta \,\,\mathbf{Kv}+\left( 1-\cos \theta \right) \mathbf{K}^2\mathbf{v}, \lVert \mathbf{K} \rVert _2=1$ (1-15)
补充一下推导过程:
矢量三重叉积,链接了平行分量和垂直分量。对于给定任意三个向量a,b,c,参考公式为:
$a×\left( b×c \right) =\left( a·c \right) b-\left( a·b \right) c$
(1-10)到(1-15)都点跨度比较大,其实中间经过了下面一个步骤:
$\mathbf{v}_{\text{rot}}=\cos \theta \mathbf{v}+\left( 1-\cos \theta \right) \left( \mathbf{k}\cdot \mathbf{v} \right) \mathbf{k}+\sin \theta \,\,\mathbf{k}\times \mathbf{v}_{\bot}\\=\mathbf{v}-\left( 1-\cos \theta \right) \left( \mathbf{k}\cdot \mathbf{k} \right) \mathbf{v}+\left( 1-\cos \theta \right) \left( \mathbf{k}\cdot \mathbf{v} \right) \mathbf{k}+\sin \theta \,\,\mathbf{k}\times \mathbf{v}\\=\mathbf{v}+\left( 1-\cos \theta \right) \left( \left( \mathbf{k}\cdot \mathbf{v} \right) \mathbf{k}-\left( \mathbf{k}\cdot \mathbf{k} \right) \mathbf{v} \right) +\sin \theta \,\,\mathbf{K}\times \mathbf{v}$
再根据矢量三重叉积就可以获得(1-15)。
将v用紧凑表达式表达
$\mathbf{v}_{\text{rot}}=\mathbf{Rv}$ (1-16)
最后获得罗德里格斯旋转方程:
$\mathbf{R}=\mathbf{I}+\sin \theta \,\,\mathbf{K}\,\,+\left( 1-\cos \theta \right) \,\,\mathbf{K}^2$ (1-17)
矩阵R是上SO(3) 旋转群(《视觉SLAM十四讲》中,将其称作为特殊正交群)中的一个元素。K是那个李群上的李代数中的一个元素。
用矩阵的指数表示:
$\mathbf{R}=\exp \left( \theta \mathbf{K} \right) =\exp \left( \theta \mathbf{k}^{\land} \right) $
为了证明最后一个等式成立,我们注意到:
$\mathbf{R}\left( \theta \right) \mathbf{R}\left( \phi \right) =\mathbf{R}\left( \theta +\phi \right) , \mathbf{R}\left( 0 \right) =\mathbf{I}$
characteristic of a one-parameter subgroup, i.e. exponential, and that the formulas match for infinitesimal θ.
For an alternative derivation based on this exponential relationship, see exponential map from$\mathfrak{s}\mathfrak{o}\left( 3 \right) $ to SO(3). For the inverse mapping, see log map from SO(3) to $\mathfrak{s}\mathfrak{o}\left( 3 \right) $.
Note that the Hodge dual of the rotation R is just $\mathbf{R}^*=-\sin \left( \theta \right) \mathbf{k}$ which allows the extraction of both the axis of rotation and the sine of the angle of the rotation from the rotation itself, with the usual ambiguity:
$\sin \left( \theta \right) =\sigma |\mathbf{R}^*|\\\mathbf{k}=-\sigma \mathbf{R}^*/|\mathbf{R}^*|$
where . The above simple expression results from the fact that the Hodge dual of$\mathbf{I}$and $\mathbf{K}^2$ are zero, and $\mathbf{K}^*=-\mathbf{k}$.
参考资料:
维基百科-罗德里格斯方程, 2020.3.7

来源:https://www.cnblogs.com/arxive/p/12439235.html