深入理解floyd算法

先上floyd算法的代码，本质上是动态规划问题
本质就是DP含有动态规划的思想，满足重叠子问题和最优子结构
dis[k][i][j]=min(dis[k-1][i][j],dis[k-1][i][k]+dis[k-1][k][j]);
我们可以发现他其实是由前k-1的状态来推出第k个点的状态之后你就会发现f[k]只与f[k-1]有关然后我们可以根据这个性质解决很多问题

for (k = 1; k <= n; k++) {
        for (i = 1; i <= n; i++) {
            for (j = 1; j <= n; j++) {
                if (dis[i][k] + dis[k][j] < dis[i][j]) {
                    dis[i][j] = dis[i][k] + dis[k][j];
                }
            }
        }
    }

这个经典代码的难点在于理解为什么k的循环在外面，这里附上一波知乎的高赞解释
在这里插入图片描述
可能部分大佬看到这段抽象的解释之后已经豁然开朗，如果还有部分大佬没有看懂的话，本菜鸡尝试用通俗的语言来翻译一下
这里给出一张简单的有向图
1->5,5->6,6->3的距离均为1，如果按照k值在最内部进行循环的话
dist[1][3]的距离无法更新，因为dist[1][3] = dist[1][6] + dist[6][3],
而dist[1][6] = dist[1][5]+dist[5][6]
即先要更新dist[1][6]之后，才能再更新dist[1][3]，而由于i，j在外侧
对于dist[1][3] 的访问先于对于dist[1][6]的访问，所以要更新dist[1][3]时,dist[1][6]还是不可达状态，也就是动态规划中的前面状态未达到最优状态就进行后续的动态规划
k在内层时先更新1，3，再更新1，6 当k在外层的时候
在这里插入图片描述 k = 5时,dist[1][5] = 1,dist[5][6] = 1,所以dist[1][6] = 1,然后更新k=6
k = 6时,dist[1][6] = 2,dist[6][3] = 1,所以dist[1][3] = 3,更新dist[1][3]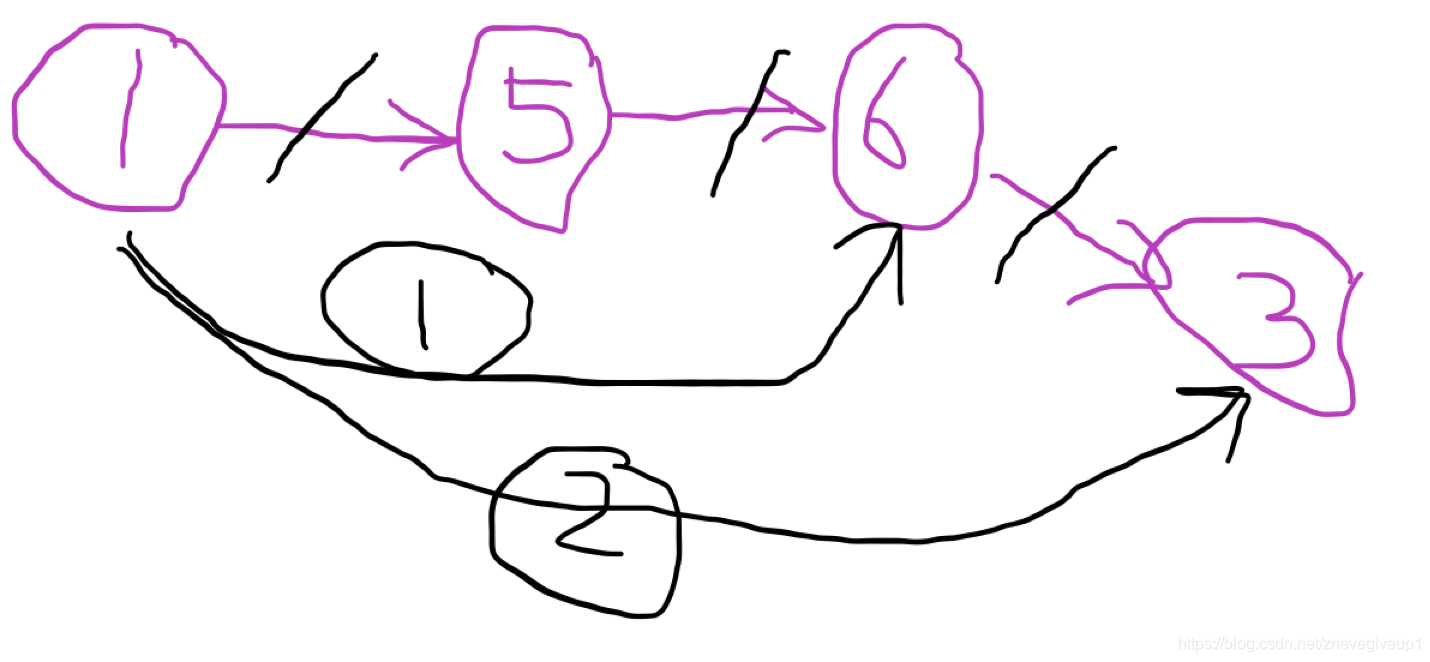
先更新以节点5为中点的最优值，再更新以节点6为中点的最优值
如果 5与6的位置倒过来，如图所示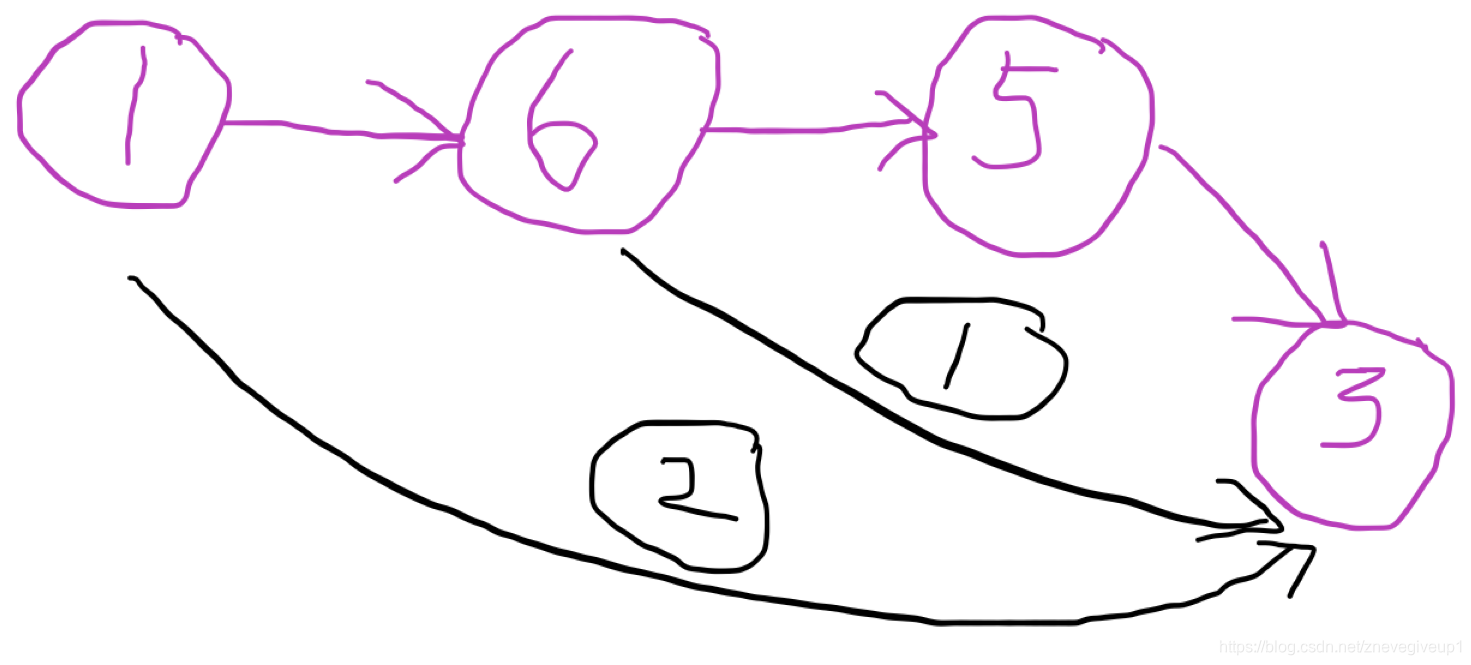
在这里插入图片描述
先更新以5为中点的最优值，得到dist[6][3],再更新以6为重点的最优值,得到dist[1][3]

来源：CSDN

作者：白袍侠客

链接：https://blog.csdn.net/znevegiveup1/article/details/104689834

标签

k-1

动态规划算法

floyd算法