总的来说这篇论文提出了ResNet架构,让训练非常深的神经网络(NN)成为了可能。
什么是残差?
“残差在数理统计中是指实际观察值与估计值(拟合值)之间的差。”如果回归模型正确的话, 我们可以将残差看作误差的观测值。”更准确地,假设我们想要找一个 xx,使得 f(x)=bf(x)=b,给定一个 xx 的估计值 x0x0,残差(residual)就是 b−f(x0)b−f(x0),同时,误差就是 x−x0x−x0
为什么需要堆叠更深的NN呢?
论文阐述道
-- 深度神经网络自然的集成了低、中、高阶特征,同时随着网络深度的提升,这些特征也会随之丰富,这些丰富的特征对于最后执行的分类或回归任务来说都是很有意义的,一般认为可以获得更好的结果;
但是,论文又指出一些问题,堆叠深层的NN存在一些问题:
-- 堆叠深层的网络后,网络的学习会变得更加的不容易,因为存在着梯度消失/爆炸问题(BN一定程度解决),会妨碍模型的收敛,使得模型不能得到很好的学习;
-- 通过实验发现,堆叠更深的网络存在着退化问题,即随着深度的增加,在分类任务中的正确率会饱和并开始迅速的下降,并且会得到更大的训练损失;
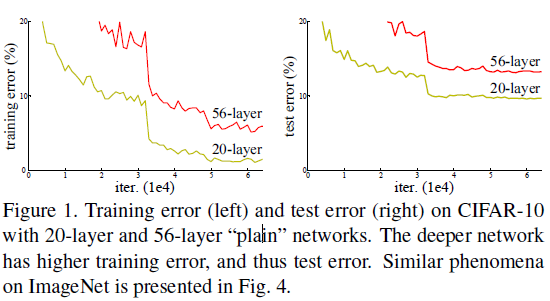
所以可以得到想要优化深层的网络结果并不容易,那么现有解决方法是怎么构造更深层的模型呢?
作者阐述了一种方法就是:增添的网络层都是恒等映射网络,同时其他的层是从已经学习的较浅的层复制而来的结构。
-- 因为都是恒等映射和从浅层模型中复制而来的,所以就可以推导出这样构造的更深层的结构的训练损失并不会高于与它对应的浅层结构;
但是同时指出: 我们现有的解决方案无法找到比构造的解决方案更好或更好的解决方案。那么有没有方法既可以有深层的网络结构,又便于网络进行训练学习呢?所以作者提出了自己的解决方案:
-- 提出了深度残差学习(deep resdual learning)架构去解决由于网络深度增加而出现的退化问题;
-- 提出网络拟合一个残差映射而不是直接拟合一个想得到的潜在的映射的思路;
具体的:
定义$\textit{H}(\textbf{x})$为想得到的潜在的映射;
堆叠非线性层去拟合另一个映射:$\textit{F}(\textbf{x}):=\textit{h}(\textbf{x})\text{}-\text{}\textbf{x}.$
那么原先的映射被重映射为:$\textit{F}(\textbf{x})\text{}+\text{}\textbf{x}.$
-- 那么如果假设一个恒等映射是做优的,那么结合上面的公式可以得到,那么直接将残差推向0比通过一些非线性层的堆叠拟合一个恒等映射更加轻松;
-- $\textit{F}(x)+x$能够通过前向神经网络和跳跃连接的结构实现,这种结构能够简单的实现恒等映射,并且不会对模型增加额外的参数和计算复杂度,能够通过SGD进行端到端的反向传播。
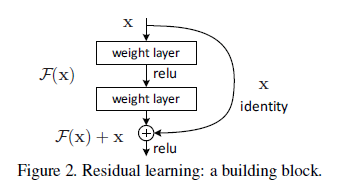
-- 深度残差网络更容易去优化,而与它相对应的朴素网络会随着深度的增加表现出更加高的训练损失;同时,深度残差网络能够更加容易的享有深度增加而带来的精确率的提升效果;
残差学习(residual learning)
--$\textit{H}(x)是作为潜在的映射而被一些堆叠的网络层就行拟合$,其中的$x$代表这些层的第一层的输入,假设多层的非线性层能够渐进的逼近复杂的函数。
--之后,之后对等的假设能够逼近残差函数,$\textit{H}(x)-x$。
-- 相比希望堆叠这些网络层去逼近$\textit{H}(x)$,我们显式的让这些网络层去逼近一个残差函数$F(x):=H(x)-x$,那么原先的函数就变成了$F(x)+x$,所以虽然这两种形式都应该能够渐进地逼近所需的函数(假设的那样),但学习的容易程度可能有所不同。
-- 图一产生的违反直觉的退化问题,我们可以根据一些推断,比如更深的网络增加的都是恒等映射表现应该不会低于相对应的浅层网络的,但是发现还是退化了,所以可以大胆的猜想,网络对于拟合恒等映射是有困难的,但是对于残差学习来说,如果恒等映射是最优的只需要把多层非线性的权重推向0就可。
-- 真实世界中,恒等映射是很难的,但是这个残差的形式或许有助于修复这个问题。
-- 如果最优函数更接近于恒等映射而不是零映射,那么求解者应该更容易找到与恒等映射相关的扰动,而不是将函数作为一个新的函数来学习。
恒等映射by shortcuts
$y = F(x,{W_{i}}+x)$
$F(x,{W_{i}})$代表残差映射而被学习,注意的是,如果输入和输出不相等的话,可以进行一个线性的映射$W_{s}$去匹配维度。
$y = F(x, {W})+W_{s}x$
残差函数$F$可以由两层或者多层表示:

整体网络结构

如虚线所示,当维度出现增加时,有两种处理办法:
-- 使用上文所提及的线性映射的方法,使用1*1的卷积去匹配维度
-- 仍然进行恒等映射,只不过使用额外的整体填充去增加维度,这样不导致额外的参数;
-- 如上图所示,当特征图进行变化时,步长都变为2;
Why resdual networks works?
梯度可以到达每一层,而在每一层之间只有少量的层,它需要进行微分,一定程度上缓解了梯度消失现象
梯度会越来越小,随着梯度的反向传播,shortcut可以帮助梯度到达每一层,反向的距离为原先的一半。

让梯度更加平缓,增强梯度传播
有点集成学习的意思,泛化性好一些
来源:https://www.cnblogs.com/ChenKe-cheng/p/11367730.html