二叉树的性质:
完全二叉树和满二叉树的概念:
二叉树的广义表表现形式: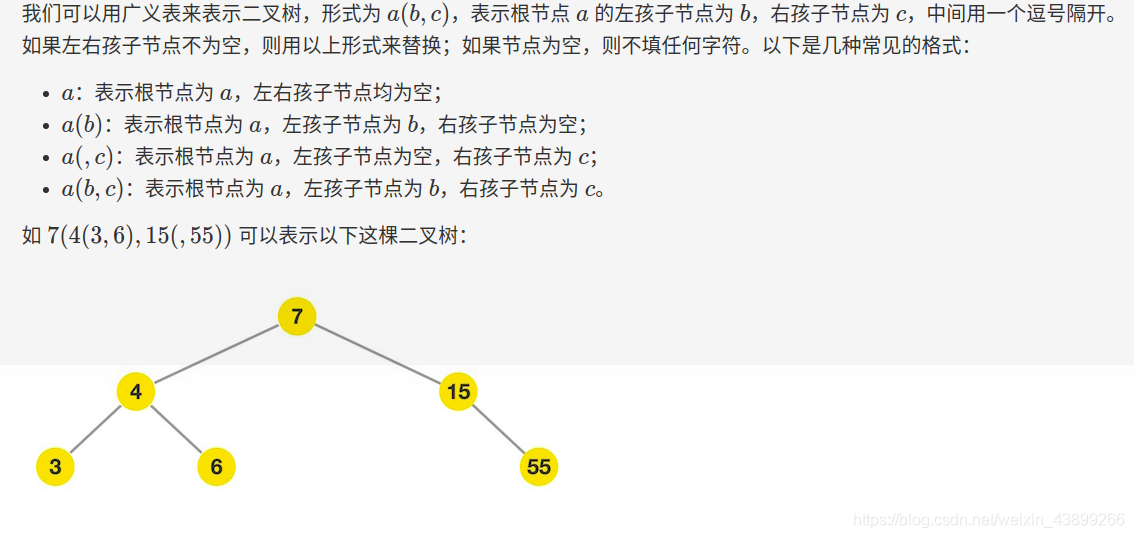
将广义表转换为二叉树(伪代码):
设置一个标记变量 k,初始为 -1;
设置一个标记节点 p;
循环遍历存储广义表的字符串 str:
如果 str[i] 是左括号:
则设置 k 为 0;
把 p 压入栈中。
否则如果 str[i] 是逗号:
则设置 k 为 1。
否则如果 str[i] 是右括号:
则栈顶元素出栈。
否则如果 str[i] 是一个字母,用节点 temp 来存储:
如果 k 为 -1:
则把 temp 作为根节点并压入栈中。
如果 k 为 0:
如果此时栈顶节点是 p,则先出栈;
然后将 temp 作为栈顶节点的左孩子;
再把 temp 压入栈中。
如果 k 为 1:
栈顶元素出栈;
将 temp 作为栈顶节点的右孩子;
再把 temp 压入栈中。
输出二叉树的广义表形式伪代码:
输出节点存储的值;
如果左孩子不为空:
输出 “(”;
递归输出左子树;
如果右孩子为空:
输出 “)”。
如果右孩子不为空:
如果左孩子为空:
输出 “(”。
输出 “,”;
递归输出右子树;
输出 “)”。
根据先序遍历和中序遍历,输出二叉树,
Node *build(char pre_str[], char in_str[], int len){
Node *p = init(pre_str[0] - ‘0’);
int pos = strchr(in_str, pre_str[0]) - in_str;
if(pos > 0){
p->lchild = build(pre_str + 1, in_str, pos);
}
if(len - pos - 1 > 0){
p->rchild = build(pre_str + pos + 1, in_str + pos + 1, len - pos - 1);
}
return p;
}
来源:CSDN
作者:algo▪Tempest
链接:https://blog.csdn.net/weixin_43899266/article/details/104338502