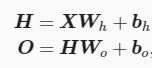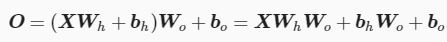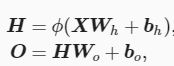多层感知机
线性回归和 softmax 回归是单层神经网络。多层感知机 (multilayer perceptron,MLP) 是多层神经网络。如图展示了一个多层感知机的神经网络图。
该网络输入和输出个数分别为4和3,含有一个隐藏层,该层中有5个隐藏单元。输入层不涉及计算,图中多层感知机的层数为2。其中隐藏层中的神经元和输入层中各个输入完全连接,输出层中的神经元和隐藏层中的各个神经元也完全连接。因此,多层感知机中的隐藏层和输出层都是全连接层。
具体来说,给定一个小批量样本 X∈R^(n×d) ,其批量大小为 n ,输入个数为 d 。假设多层感知机只有一个隐藏层,其中隐藏单元个数为 h 。记隐藏层的输出(也称为隐藏层变量或隐藏变量)为 H ,有 H∈R^(n×h) 。因为隐藏层和输出层均是全连接层,可以设隐藏层的权重参数和偏差参数为 Wh∈R^(d×h)和 bh∈R^(1×h) ,输出层的权重和偏差参数分别为 Wo∈R^(h×q) 和 bo∈R^(1×q) 。
含单隐藏层的多层感知机的设计。其输出 O∈R^(n×q) 的计算为:
也就是将隐藏层的输出直接作为输出层的输入。如果将以上两个式子联立起来,可以得到:
从联立后的式子可以看出,虽然神经网络引入了隐藏层,却依然等价于一个单层神经网络:其中输出层权重参数为 WhWo ,偏差参数为 bhWo+bo 。不难发现,即便再添加更多的隐藏层,以上设计依然只能与仅含输出层的单层神经网络等价。
激活函数
上述问题的根源在于全连接层只是对数据做仿射变换,而多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法是引入非线性变换,例如对隐藏变量使用按元素运算的非线性函数进行变换,然后再作为下一个全连接层的输入。这个非线性函数被称为激活函数。
早期研究神经网络主要采用sigmoid函数或者tanh函数,输出有界,很容易充当下一层的输入。
近些年Relu函数及其改进型(如Leaky-ReLU、P-ReLU、R-ReLU等)在多层神经网络中应用比较多。
关于激活函数的选择
ReLu函数是一个通用的激活函数,目前在大多数情况下使用。但是,ReLU函数只能在隐藏层中使用。用于分类器时,sigmoid函数及其组合通常效果更好。由于梯度消失问题,有时要避免使用sigmoid和tanh函数。在神经网络层数较多的时候,最好使用ReLu函数,ReLu函数比较简单计算量少,而sigmoid和tanh函数计算量大很多。在选择激活函数的时候可以先选用ReLu函数如果效果不理想可以尝试其他激活函数。
多层感知机就是含有至少一个隐藏层的由全连接层组成的神经网络,且每个隐藏层的输出通过激活函数进行变换。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。以单隐藏层为例并沿用本节之前定义的符号,多层感知机按以下方式计算输出:
其中 ϕ 表示激活函数。在分类问题中,我们可以对输出 O 做softmax运算,并使用softmax回归中的交叉熵损失函数。 在回归问题中,我们将输出层的输出个数设为1,并将输出 O 直接提供给线性回归中使用的平方损失函数。
来源:CSDN
作者:P_B_Y
链接:https://blog.csdn.net/P_B_Y/article/details/104311783