[python机器学习及实践(6)]Sklearn实现主成分分析（PCA）

1.PCA原理

主成分分析（Principal Component Analysis，PCA），是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。

PCA算法：

2.PCA的实现

数据集：

64维的手写数字图像

代码：

#coding=utf-8
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from matplotlib import pyplot as plt
from sklearn.svm import LinearSVC
from sklearn.metrics import classification_report

#1.初始化一个线性矩阵并求秩
M = np.array([[1,2],[2,4]])   #初始化一个2*2的线性相关矩阵
np.linalg.matrix_rank(M,tol=None)  # 计算矩阵的秩

#2.读取训练数据与测试数据集。
digits_train = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tra', header=None)
digits_test = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/optdigits/optdigits.tes', header=None)
print digits_train.shape   #(3823, 65)    3000+个样本，每个数据由64个特征，1个标签构成
print digits_test.shape    #(1797, 65)

#3将数据降维到2维并可视化

# 3.1 分割训练数据的特征向量和标记
X_digits = digits_train[np.arange(64)]         #得到64位特征值
y_digits = digits_train[64]                    #得到对应的标签

#3.2 PCA降维：降到2维
estimator = PCA(n_components=2)
X_pca=estimator.fit_transform(X_digits)

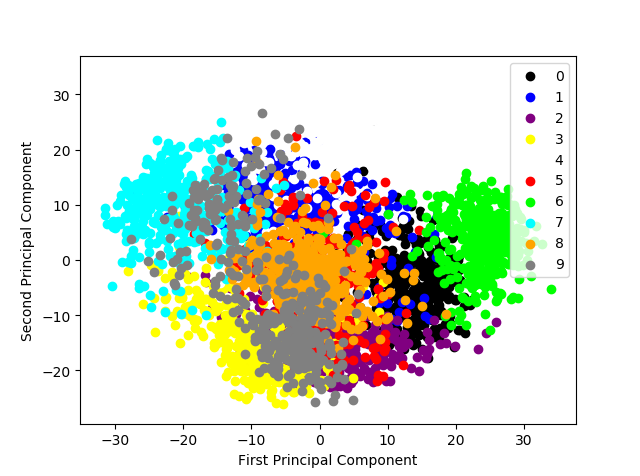
#3.3 显示这10类手写体数字图片经PCA压缩后的2维空间分布
def plot_pca_scatter():
    colors = ['black', 'blue', 'purple', 'yellow', 'white', 'red', 'lime', 'cyan', 'orange', 'gray']
    for i in xrange(len(colors)):
        px = X_pca[:, 0][y_digits.as_matrix() == i]
        py = X_pca[:, 1][y_digits.as_matrix() == i]
        plt.scatter(px, py, c=colors[i])
    plt.legend(np.arange(0, 10).astype(str))
    plt.xlabel('First Principal Component')
    plt.ylabel('Second Principal Component')
    plt.show()
plot_pca_scatter()

# 4.用SVM分别对原始空间的数据（64维）和降到20维的数据进行训练，预测

# 4.1 对训练数据／测试数据进行特征向量与分类标签的分离
X_train = digits_train[np.arange(64)]
y_train = digits_train[64]
X_test = digits_test[np.arange(64)]
y_test = digits_test[64]

#4.2 用SVM对64维数据进行进行训练
svc = LinearSVC()  # 初始化线性核的支持向量机的分类器
svc.fit(X_train,y_train)
y_pred = svc.predict(X_test)

#4.3 用SVM对20维数据进行进行训练
estimator = PCA(n_components=20)   # 使用PCA将原64维度图像压缩为20个维度
pca_X_train = estimator.fit_transform(X_train)   # 利用训练特征决定20个正交维度的方向，并转化原训练特征
pca_X_test = estimator.transform(X_test)

psc_svc = LinearSVC()
psc_svc.fit(pca_X_train,y_train)
pca_y_pred = psc_svc.predict(pca_X_test)

#5.获取结果报告
#输出用64维度训练的结果
print svc.score(X_test,y_test)
print classification_report(y_test,y_pred,target_names=np.arange(10).astype(str))

#输出用20维度训练的结果
print psc_svc.score(pca_X_test,y_test)
print classification_report(y_test,pca_y_pred,target_names=np.arange(10).astype(str))

运行结果：

1）将数据压缩到两维，在二维平面的可视化。

2）SVM对64维和20维数据的训练结果

0.9220923761825265
precision recall f1-score support

0 0.99 0.98 0.99 178
1 0.97 0.76 0.85 182
2 0.99 0.98 0.98 177
3 1.00 0.87 0.93 183
4 0.95 0.97 0.96 181
5 0.90 0.97 0.93 182
6 0.99 0.97 0.98 181
7 0.99 0.90 0.94 179
8 0.67 0.97 0.79 174
9 0.90 0.86 0.88 180

avg / total 0.94 0.92 0.92 1797

0.9248747913188647
precision recall f1-score support

0 0.97 0.96 0.96 178
1 0.88 0.90 0.89 182
2 0.96 0.99 0.97 177
3 0.99 0.91 0.95 183
4 0.92 0.96 0.94 181
5 0.87 0.96 0.91 182
6 0.98 0.97 0.98 181
7 0.98 0.89 0.93 179
8 0.91 0.83 0.86 174
9 0.83 0.88 0.85 180

avg / total 0.93 0.92 0.93 1797

结论：降维后的准确率降低，但却用了更少的维度。

3.PCA的优缺点

PCA算法的主要优点有：

1）仅仅需要以方差衡量信息量，不受数据集以外的因素影响。　

2）各主成分之间正交，可消除原始数据成分间的相互影响的因素。

3）计算方法简单，主要运算是特征值分解，易于实现。

PCA算法的主要缺点有：

1）主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。

2）方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。

来源：https://www.cnblogs.com/youngsea/p/9334773.html

标签