冒泡排序

算法思想

冒泡排序是最简单的排序算法之一，在给定的序列中，依次的比较两个数字，如果顺序错误就交换两个数字的位置。然后重复步骤，直到整个给定的序列符合要求位置。

算法步骤:

比较相邻的两个数字，如果第一个比第二个数字大，那么交换两个数字的位置；否则，继续下一个位置的比较
对每一对相邻的元素做同样的工作，遍历完整个序列以后，最后的数字一定是最大的数字
针对所有的数字，重复以上步骤，除了最后一个（这里的最后一个不是特指所有给出的序列的最后一个，而是相对于上次比较的最后一个，是相对的位置）
重复1~3，直到整个给定的序列排序完成

下面结合动画，可以更加清楚的理解上述的算法步骤：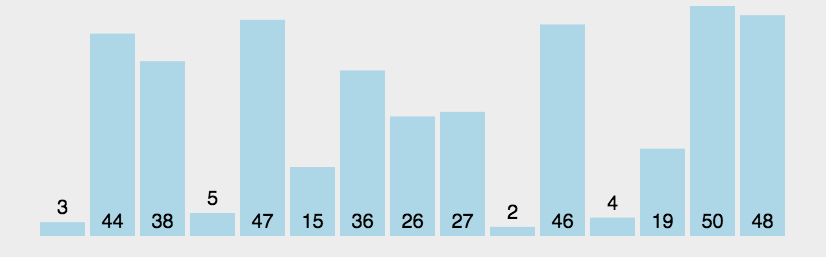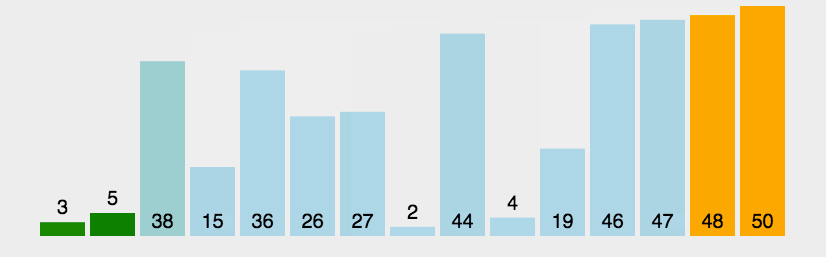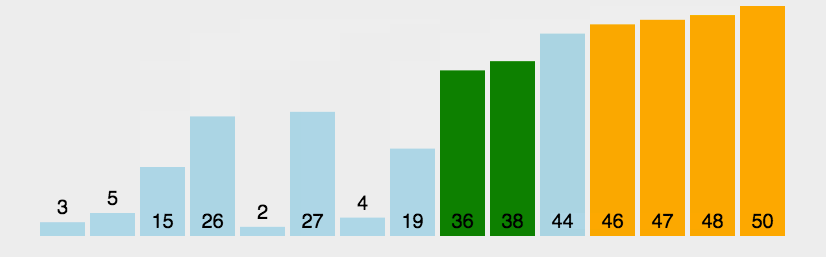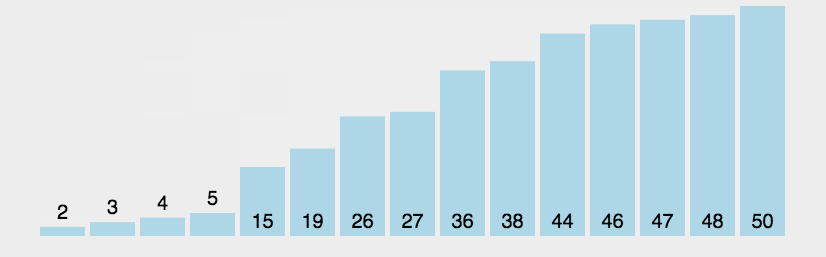
在这里插入图片描述
从上面的算法步骤及动画中，可以分析冒泡排序的时间复杂度是 $O(n^2)$ ，并且是一种稳定的排序算法（如何决定算法是否稳定，如果有两个相同的数字，比如 arr=[3,4,1,3]，如果排序完成以后，下标为0的3，仍然在下标为3的3的前面，就表示是稳定的），整个排序过程中只需要有限个临时遍历用于数据的交换，所以空间复杂度为 $O(1)$ 。

代码实现

#include <iostream>
#include <vector>

using namespace std;

void bubbleSrot(vector<int>& vec) {
	// 如果序列的长度小于2个，那么表示不需要排序，直接返回
    if (vec.size() < 2) {
		return;
	}
	// 外层循环表示需要排序的元素的长度，内层循环表示从开始一直到外层循环的长度才终止比较
	for (int i = vec.size() - 1; i > 0; i--) {
		for (int j = 0; j < i; j++) {
            // 如果前一个数字比较大，那么把两个数字的位置交换
			if (vec[j] > vec[j + 1]) {  
				int temp = vec[j];
				vec[j] = vec[j + 1];
				vec[j + 1] = temp;
			}
		}
	}
}

/*
* 验证算法
*/
int main() {
	vector<int> arr = { 3,44,38,5,47,15,36,26,27,2,46,4,19,50,48 };
	bubbleSrot(arr);
    // 输出排序结果
	for (int i = 0; i < arr.size(); i++) {
		cout << arr[i] << " ";
	}
	cout << endl;

	return 0;
}

冒泡排序优化

试想一下，如果有这样一个序列 arr=[6,1,2,3,4,5]，执行一轮循环以后，最后一个元素是最大的，并且冒泡排序是一种稳定的算法，所以第一轮的输出结果是 arr=[1,2,3,4,5,6]，此时整个序列已经完成排序了，但是根据我们上述的算法步骤，它还是需要继续向下执行。那么是否可以优化一下，当数字已经完成排序的时候结束循环呢？答案是肯定的嘛，如果不可以我还怎么写下面的内容 😄.

其实优化的方法很简单，只需要定义一个标志位，判断该轮循环的过程中数据时候还有交换，如果没有交换那么表示整个序列已经排序完成，即arr=[6,1,2,3,4,5]，经过一个外层循环最有一个位置的数字已经拍好了，那么待排序的数字为[1,2,3,4,5]，这个序列很明显是拍好了，不需要交换，那么标志位就没有办法置位，通过检测标志位的状态就可以提前结束循环，下面可以看一下代码，很简单，只需要添加一个变量。

代码如下：

#include <iostream>
#include <vector>

using namespace std;

void bubbleSrotImprove(vector<int>& vec) {
	// 如果数据的数量小于2，表示不需要排序直接返回
    if (vec.size() < 2) {
		return;
	}

	int time = 1; // 记录循环的次数
	for (int i = vec.size() - 1; i > 0; i--) {
		cout << "第" << time << "次循环" << endl;  // 输出需要的次数
		bool flag = true;     // 定义一个标志位，用于记录是否有数据交换
		for (int j = 0; j < i; j++) {
			if (vec[j] > vec[j + 1]) {
				flag = false;    // 标志位置位
				int temp = vec[j];
				vec[j] = vec[j + 1];
				vec[j + 1] = temp;
			}
		}
        // 判断是否排序完成
		if (flag) {
			cout << "第" << time << "次排序，数据已经排列完成" << endl;
			break;
		}
		time++;  // 循环次数加1
	}

}


int main() {
	vector<int> arr = { 6,1,2,3,4,5 };
	bubbleSrotImprove(arr);
	for (int i = 0; i < arr.size(); i++) {
		cout << arr[i] << " ";
	}
	cout << endl;

	return 0;
}

输出的结果如下：
在这里插入图片描述
去掉打印信息，优化的冒泡排序函数，代码如下：

void bubbleSrotImprove(vector<int>& vec) {
	if (vec.size() < 2) {
		return;
	}

	for (int i = vec.size() - 1; i > 0; i--) {
		bool flag = true;
		for (int j = 0; j < i; j++) {
			if (vec[j] > vec[j + 1]) {
				flag = false;
				int temp = vec[j];
				vec[j] = vec[j + 1];
				vec[j + 1] = temp;
			}
		}
		if (flag) {
			break;
		}
	}
}

总结

稳定性：稳定
时间复杂度： $O(n^2)$
空间复杂度： $O(1)$

欢迎大家关注我的个人公众号，同样的也是和该博客账号一样，专注分享技术问题，我们一起学习进步
在这里插入图片描述

来源：CSDN

作者：黑暗主宰

链接：https://blog.csdn.net/EngineerHe/article/details/104107058

标签

冒泡排序