BFS
什么时候使用BFS
- 图的遍历 traversal in graph
1.1 层级遍历 level order traversal
1.2 由点及面 connected component
1.3 拓扑排序 topological sorting - 最短路径 shortest path in simple graph
2.1 仅限简单图求最短路径
2.2 即,途中每条边长度都是 1,且没有方向
最短路径问题可以用BFS或者DP解决
最长路径问题可以用DFS或者DP解决
BFS还有一个东西很重要就是是否需要分层遍历,如果需要分层遍历,需要添加一行代码同时添加一个 for loop。比如说例题 Zombie in Matrix, 例题 Knight shortest path
补充知识
BFS采用 FIFO Queue 实现,DFS采用 Stack 实现。
在JAVA中,Queue 是一个接口,具体实现可以采用LinkedList.
LinkedList API
remove(), Item, Retrieves and removes the head (first element) of this list.
size(), int, Returns the number of elements in this list
isEmpty(), boolean, Returns whether the list is empty
offer(Item), boolean, Adds the specified element as the tail (last element) of this list.
poll(), Item, Retrieves and removes the head (first element) of this list.
利用LinkedList 实现 FIFO Queue 可以使用 offer(), poll()组合,从最后面加入元素,从最前面取出元素;或者使用 add(), add 和 offer() 是一样的。
add(Item), boolean, Appends the specified element to the end of this list.
add(index, Item), void, Inserts the specified element at the specified position in this list.
1 BFS in binary tree
例题 102. Binary Tree Level Order Traversal
Given a binary tree, return the level order traversal of its nodes’ values. (ie, from left to right, level by level).
For example:
Given binary tree [3,9,20,null,null,15,7],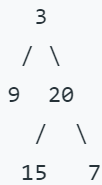
return its level order traversal as:
[
[3],
[9,20],
[15,7]
]
solution
采用FIFO Queue实现BFS,需要注意的是在每一次确定每一层的大小时,int size = fifo.size();,必须放在 for 循环的外面
for 循环确保了分层输出 List 结果,如果去掉 for 循环,其实得到的结果是一样的,但是不能明确分层
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> result = new ArrayList<>();
if (root == null) return result;
// fifo queue
Queue<TreeNode> fifo = new LinkedList<>();
fifo.offer(root);
while (!fifo.isEmpty()) {
int size = fifo.size();
ArrayList<Integer> list = new ArrayList<>();
for (int i = 0; i < size; i++) {
TreeNode cur = fifo.poll();
if (cur.left != null) {
fifo.offer(cur.left);
}
if (cur.right != null) {
fifo.offer(cur.right);
}
list.add(cur.val);
}
result.add(list);
}
return result;
}
}
还可以采用 recursion 的解法
class Solution {
List<List<Integer>> levels = new ArrayList<List<Integer>>();
public void helper(TreeNode node, int level) {
// start the current level
if (levels.size() == level)
levels.add(new ArrayList<Integer>());
// fulfil the current level
levels.get(level).add(node.val);
// process child nodes for the next level
if (node.left != null)
helper(node.left, level + 1);
if (node.right != null)
helper(node.right, level + 1);
}
public List<List<Integer>> levelOrder(TreeNode root) {
if (root == null) return levels;
helper(root, 0);
return levels;
}
}
例题 binary tree 序列化 serialization
序列化就是指将内存中结构化的数据变成字符串的过程,反之,反序列化就是把字符串变成结构化数据的过程
2 BFS in graph
和树的区别是:
路径上存在区别,tree 中总是从 root 到 leaf,但是 graph 中不存在 parent-child 关系。所以在遍历 graph 的时候需要存储一下当前已经 visit 的节点。
图中有 N 个点 M 条边
时间复杂度
,其中 M 最大为 ,所以最坏情况下的世家复杂度为
例题 261. Graph Valid Tree
Given n nodes labeled from 0 to n-1 and a list of undirected edges (each edge is a pair of nodes), write a function to check whether these edges make up a valid tree.
Example 1:
Input: n = 5, and edges = [[0,1], [0,2], [0,3], [1,4]]
Output: true
Example 2:
Input: n = 5, and edges = [[0,1], [1,2], [2,3], [1,3], [1,4]]
Output: false
Note: you can assume that no duplicate edges will appear in edges. Since all edges are undirected, [0,1] is the same as [1,0] and thus will not appear together in edges.
tree 的条件是有 n 个节点, n-1 个边, 同时所有点连通
solution
class Solution {
public boolean validTree(int n, int[][] edges) {
if (n != edges.length + 1) {
return false;
}
Queue<Integer> fifo = new LinkedList<Integer>();
// set stores the nodes that are connected
HashSet<Integer> set = new HashSet<>();
Map<Integer, Set<Integer>> graph = graphGen(n, edges);
fifo.add(0);
set.add(0);
while(!fifo.isEmpty()) {
int node = fifo.poll();
for (Integer neighbor : graph.get(node)) {
// if the node, neighbor, is already added to the set, continue
if (set.contains(neighbor)) {
continue;
}
fifo.offer(neighbor);
set.add(neighbor);
}
}
return (set.size() == n);
}
public Map<Integer, Set<Integer>> graphGen(int n, int[][] edges) {
// generate the graph using the edges info
// Use HashMap to map neighbors to a node
Map<Integer, Set<Integer>> graph = new HashMap<>();
for (int i = 0; i < n; i++) {
graph.put(i, new HashSet<Integer>());
}
for (int i = 0; i < edges.length; i++) {
graph.get(edges[i][0]).add(edges[i][1]);
graph.get(edges[i][1]).add(edges[i][0]);
}
return graph;
}
}
例题 133. Clone Graph
Given a reference of a node in a connected undirected graph, return a deep copy (clone) of the graph. Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.
Note:
- The number of nodes will be between 1 and 100.
- The undirected graph is a simple graph, which means no repeated edges and no self-loops in the graph.
- Since the graph is undirected, if node p has node q as neighbor, then node q must have node p as neighbor too.
- You must return the copy of the given node as a reference to the cloned graph.
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> neighbors;
public Node() {}
public Node(int _val,List<Node> _neighbors) {
val = _val;
neighbors = _neighbors;
}
};
*/
class Solution {
public Node cloneGraph(Node node) {
if (node == null) {
return node;
}
ArrayList<Node> nodes = getNodes(node);
// HashMap is used to store the old nodes and their according new nodes.
HashMap<Node, Node> map = new HashMap<>();
for (Node tmp : nodes) {
map.put(tmp, new Node(tmp.val, new ArrayList<Node>()));
}
for (Node tmp : nodes) {
Node newNode = map.get(tmp);
for (Node neighbor : tmp.neighbors) {
Node newNeighbor = map.get(neighbor);
newNode.neighbors.add(newNeighbor);
}
}
return map.get(node);
}
// return all the nodes in the graph
public ArrayList<Node> getNodes(Node node) {
Queue<Node> queue = new LinkedList<>();
HashSet<Node> set = new HashSet<>();
queue.offer(node);
set.add(node);
while(!queue.isEmpty()) {
Node cur = queue.poll();
for (Node tmp : cur.neighbors) {
if (!set.contains(tmp)) {
set.add(tmp);
queue.offer(tmp);
}
}
}
return new ArrayList<Node>(set);
}
}
能用 BFS 解决的问题一定不要用 DFS。
Topological Sorting
可以用 DFS 但是不建议,采用 BFS 最合适
Topological sorting 从名字上听起来像是排序问题,实际上是判断 graph 中是否存在 loop。
例题 topological-sorting
给定一个有向图,图节点的拓扑排序被定义为:
- 对于每条有向边A–> B,则A必须排在B之前
- 拓扑排序的第一个节点可以是任何在图中没有其他节点指向它的节点
找到给定图的任一拓扑排序
class Solution {
public ArrayList<Node> topoSort(ArrayList<Node> graph) {
ArrayList<Node> order new ArrayList<>();
if (graph == null) {
return order;
}
// calculate the indegree of each node
HashMap<Node, Integer> inDegree = getIndegree(graph);
// get the starting nodes that have 0 indegree
ArrayList<Node> startNodes = getStartNodes(inDegree, graph);
// use bfs to find the topological order
order = bfs(inDegree, startNodes);
// check out whether the length of topological equals to the number of nodes in the graph
// if not, there is loop in the graph
if (order.size() == graph.size()) {
return order;
}
return null;
}
public ArrayList<Node> getStartNodes(HashMap<Node, Integer> inDegree, ArrayList<Node> graph) {
ArrayList<Node> nodes = new ArrayList<>();
for (Node node : graph) {
if (inDegree.get(node) == 0) {
nodes.add(node);
}
}
return nodes;
}
public HashMap<Node, Integer> getIndegree(ArrayList<Node> graph) {
HashMap<Node, Integer> inDegree = new HashMap<>();
for (Node node : graph) {
inDegree.put(node, 0);
}
for (Node node : graph) {
for (Node neighbor : node.neighbors) {
inDegree.put(neighbor, inDegree.get(neighbor) + 1);
}
}
return inDegree;
}
public ArrayList<Node> bfs(HashMap<Node, Integer> inDegree, ArrayList<Node> startNodes) {
ArrayList<Node> order = new ArrayList<>();
Queue<Node> fifo = new LinkedList<>();
// add the start nodes into the fifo queue
for (Node node : startNodes) {
order.add(node);
fifo.offer(node);
}
while (!fifo.isEmpty()) {
Node ndoe = fifo.poll();
for (Node neighbor : node.neighbors) {
inDegree.put(neighbor, inDegree.get(neighbor) - 1);
if (inDegree.get(neighbor) == 0) {
fifo.offer(neighbor);
order.add(neighbor);
}
}
}
return order;
}
}
3 BFS in 2D grid (matrix)
2D grid (matrix) 是一种特殊的 graph, 每一个格子就相当于 graph 中的一个点。连通情况有两种: 1 四连通:上下左右 2 八连通:额外包括左上左下右上右下
2D grid (matrix) 有 R 个行,C 个列,共有 个点, 条边
2D grid (matrix) 的 BFS 时间复杂度为
例题 200. Number of Islands
Given a 2d grid map of '1’s (land) and '0’s (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example 1:
Input:
11110
11010
11000
00000
Output: 1
Example 2:
Input:
11000
11000
00100
00011
Output: 3
采用 BFS 来进行搜索,每当发现一个值为 ‘1’ 的点,找到它所有相邻值为 ‘1’ 的点并将值修改为 ‘0’,同时将 island 个数加一。
需要注意的是将值改为 ‘0’ 的时间与将这个加入到 FIFO queue 的时间关系,应该先把值改为 ‘0’,然后再加入 FIFO queue,否则很可能会影响后面的计算。
class Solution {
public int numIslands(char[][] grid) {
if (grid == null || grid.length == 0 || grid[0].length == 0) {
return 0;
}
int n = grid.length;
int m = grid[0].length;
int island = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == '1') {
markBFS(grid, i ,j);
island++;
}
}
}
return island;
}
public void markBFS(char[][] grid, int i, int j) {
Queue<point> fifo = new LinkedList<>();
fifo.offer(new point(i,j));
grid[i][j] = '0';
int[] dx = {0, 0, 1, -1};
int[] dy = {1, -1, 0, 0};
while (!fifo.isEmpty()) {
point cur = fifo.poll();
for (int k = 0; k < 4; k++) {
point neighbor = new point(cur.x + dx[k], cur.y + dy[k]);
if (!inBound(grid, neighbor)) {
continue;
}
if (grid[neighbor.x][neighbor.y] == '1') {
// change the value to '0', then add it to the FIFO queue
grid[neighbor.x][neighbor.y] = '0';
fifo.offer(neighbor);
}
}
}
}
public boolean inBound(char[][] grid, point pt) {
int n = grid.length;
int m = grid[0].length;
if (pt.x < 0 || pt.x >= n) {
return false;
}
if (pt.y < 0 || pt.y >= m) {
return false;
}
return true;
}
class point {
int x;
int y;
public point(int x, int y) {
this.x = x;
this.y = y;
}
}
}
2D grid (matrix) 分层遍历
例题 Zombie in Matrix
Given a 2D grid, each cell is either a wall 2, a zombie 1 or people 0 (the number zero, one, two).Zombies can turn the nearest people(up/down/left/right) into zombies every day, but can not through wall. How long will it take to turn all people into zombies? Return -1 if can not turn all people into zombies.
Example 1:
Input:
[[0,1,2,0,0],
[1,0,0,2,1],
[0,1,0,0,0]]
Output: 2
Example 2:
Input:
[[0,0,0],
[0,0,0],
[0,0,1]]
Output: 4
class Solution {
public int PEOPLE = 0;
public int ZOMBIE = 1;
public int WALL = 2;
public int zombie (int[][] grid) {
if (grid == null || grid.length == 0) {
return 0;
}
int result = 0;
int n = grid.length;
int m = grid[0].length;
int people = 0;
Queue<cell> fifo = new LinkedList<>();
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == PEOPLE) {
prople++;
} else if (grid[i][j] == ZOMBIE) {
fifo.offer(new cell(i,j));
}
}
}
if (prople == 0) {
return 0;
}
int[] dx = {0, 0, 1, -1};
int[] dy = {1, -1, 0, 0};
while (!fifo.isEmpty()) {
int size= fifo.size();
for (int i = 0; i < size; i++) {
cell cur = fifo.poll();
for (int j = 0; j < 4; j++) {
cell neighbor = new cell(cur.x + dx[j], cur.y + dy[j]);
if (inBound(neighbor, grid)) {
if (grid[neighbor.x][neighbor.y] == PEOPLE) {
grid[neighbor.x][neighbor.y] = ZOMBIE;
people--;
fifo.offer(neighbor);
}
}
}
}
result++;
if (people == 0) {
return result;
}
}
return -1
}
public boolean inBound(cell cut, int[][] grid) {
int n = grid.length;
int m = grid[0].length;
if (cur.x < 0 || cur.x >= n) {
return false;
}
if (cur.y < 0 || cur.y >= m) {
return false;
}
return true;
}
class cell {
public int x;
public int y;
public cell(int x, int y) {
this.x = x;
this.y = y;
}
}
}
例题 Knight shortest path
Given a knight in a chessboard (a binary matrix with 0 as empty and 1 as barrier) with a source position, find the shortest path to a destination position, return the length of the route.
Return -1 if destination cannot be reached.
source and destination must be empty.
Knight can not enter the barrier.
Path length refers to the number of steps the knight takes.
Clarification
If the knight is at (x, y), he can get to the following positions in one step:
(x + 1, y + 2)
(x + 1, y - 2)
(x - 1, y + 2)
(x - 1, y - 2)
(x + 2, y + 1)
(x + 2, y - 1)
(x - 2, y + 1)
(x - 2, y - 1)
Example 1:
Input:
[[0,0,0],
[0,0,0],
[0,0,0]]
source = [2, 0] destination = [2, 2]
Output: 2
Explanation:
[2,0]->[0,1]->[2,2]
Example 2:
Input:
[[0,1,0],
[0,0,1],
[0,0,0]]
source = [2, 0] destination = [2, 2]
Output:-1
/*
class Point {
public int x;
public int y;
public Point() {
this.x = 0;
this.y = 0;
}
public Point(int x, int y) {
this.x = x;
this.y = y;
}
}
*/
class Solution {
public int shortestPath(boolean[][] grid, Point source, Point destination) {
if (grid == null) {
return 0;
}
if (source.x == destination.x && source.y == destination.y) {
return 0;
}
if (!isValid(source, grid) || !isValid(destination, grid)) {
return 0;
}
Queue<Point> fifo = new LinkedList<>();
fifo.offer(source);
int[] dx = {1, 1, 2, 2, -1, -1, -2, -2};
int[] dy = {2, -1, 1, -1, 2, -2, 1, -1};
int step = 0;
while (!fifo.isEmpty()) {
int size = fifo.size();
step++;
for (int i = 0; i < size; i++) {
Point cur = fifo.poll();
for (int j = 0; j < 8; j++) {
Point neighbor = new Point(cur.x + dx[j], cur.y + dy[j]);
if (!isValid(neighbor, grid)) {
continue;
}
if (neighbor.x == destination.x && neighbor.y == destination.y) {
return step;
}
if (!fifo.contains(neighbor)) {
fifo.offer(neighbor);
}
}
}
}
return -1;
}
public boolean isValid(Point point, boolean[][] grid) {
// a point is valid if it is within the bound and it is empty
int m = grid.length;
int n = grid[0].length;
if (point.x < 0 || point.x >= m) {
return false;
}
if (point.y < 0 || point.y >= n) {
return false;
}
return !grid[point.x][point.y];
}
}
来源:CSDN
作者:TechJungle
链接:https://blog.csdn.net/weixin_43876026/article/details/103752275