树链剖分 | 易学教程

题目描述

如题，已知一棵包含N个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：

操作1：格式： 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z

操作2：格式： 2 x y 表示求树从x到y结点最短路径上所有节点的值之和

操作3：格式： 3 x z 表示将以x为根节点的子树内所有节点值都加上z

操作4：格式： 4 x 表示求以x为根节点的子树内所有节点值之和

输入

第一行包含4个正整数N、M、R、P，分别表示树的结点个数、操作个数、根节点序号和取模数（即所有的输出结果均对此取模）。

接下来一行包含N个非负整数，分别依次表示各个节点上初始的数值。

接下来N-1行每行包含两个整数x、y，表示点x和点y之间连有一条边（保证无环且连通）

接下来M行每行包含若干个正整数，每行表示一个操作，格式如下：

操作1： 1 x y z

操作2： 2 x y

操作3： 3 x z

操作4： 4 x

输出

输出包含若干行，分别依次表示每个操作2或操作4所得的结果（对P取模）

样例输入

样例输出

2
21

提示

对于100%的数据：N<=100000，M<=100000

输入的每一个数均小于2147483647

重儿子：siz[u]为v的子节点中siz值最大的，那么u就是v的重儿子
轻儿子：v的其它子节点
重边：点v与其重儿子的连边
轻边：点v与其轻儿子的连边
重链：由重边连成的路径
轻链：轻边

size[v]表示以v为根的子树的节点数

dep[v]表示v的深度(根深度为1)

top[v]表示v所在的链的顶端节点

fa[v]表示v的父亲

son[v]表示与v在同一重链上的v的儿子节点（姑且称为重儿子）

dfs[v]表示v的dfs序

dfsn记录此时遍历到的第几个点

dfs1：把fa、dep、size、son求出来，比较简单，略过。
dfs2：⒈对于v，当son[v]存在（即v不是叶子节点）时，显然有top[son[v]] = top[v]。

线段树中，v应当在v的父亲的后面。此时，为了使同一条重链上的各个点线段树中连续分布，应当先进行dfs2(son[v])；
⒉对于v的各个轻儿子u，显然有top[u] = u。dfs2(u)；

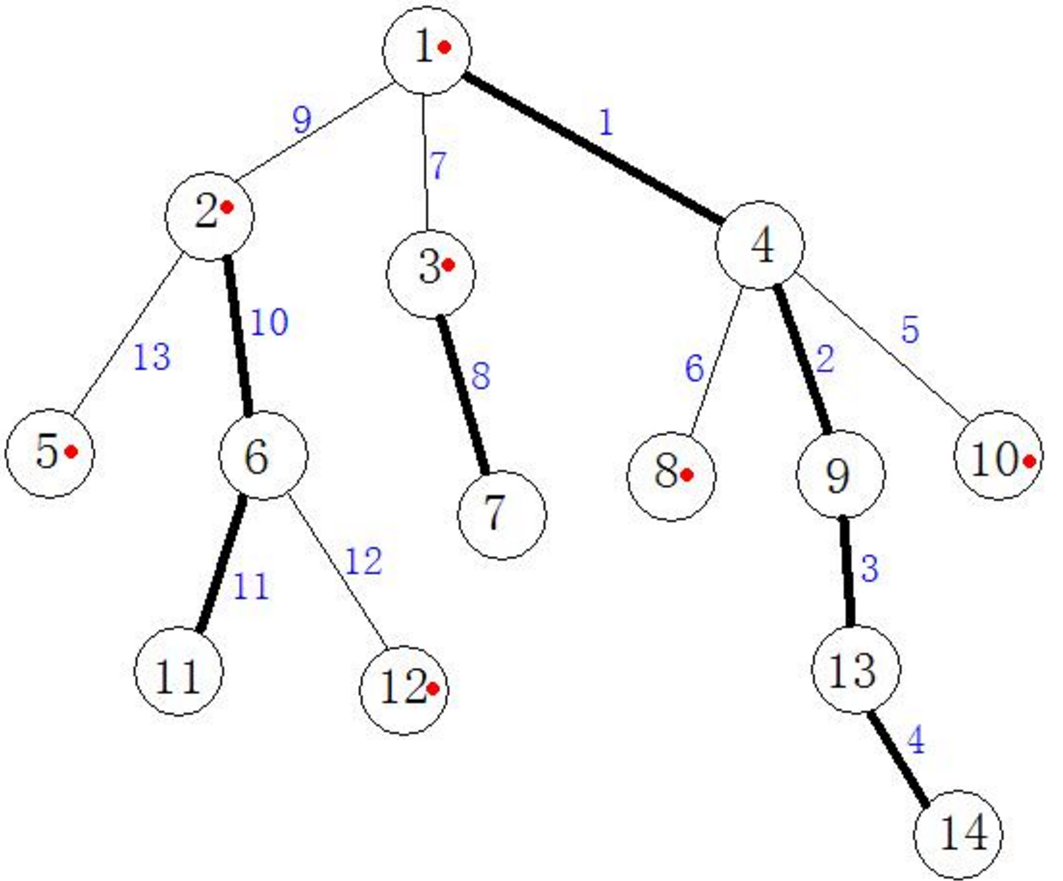
如右图所示，较粗的为重边，较细的为轻边。节点编号旁边有个红色点的表明该节点是其所在链的顶端节点。边旁的蓝色数字表示该边在线段树中的位置。图中1-4-9-13-14为一条重链。
按dfs序排好后的点：1，4，9，13，14，8，10，2，6，11，12，5，3，7,按这个数据建立线段树

观察后发现，每一条链的点在一起，每一个点的子树也在一起
操作一：x=10和y=11两个点，top[11]=2,dep[top[11]]=2,top[10]=10,dep[top[10]]=3,

dep[top[11]]<dep[top[10]] x=fa[top[10]]=4,y=11;在线段树中更改dfs[top[10]]~dfs[10]

　　　　　接下来同理，x=4,y=1 ,4与1在同一条链上，结束

操作二：x=2的子树更改dfs[2]~dfs[2]+size[2]-1

操作三：与一同理。操作四：与二同理

#include<iostream> 
#include<cstdio> 
using namespace std; 
long long lazy[400000],sum[400000];int l[400000],r[400000],head[100001],k=0,dfsn=0,mod; 
int fa[100001],dep[100001],size[100001],son[100001],top[100001],dfs[100001],a[100001]; 
struct data{int to,next;}g[200001]; 
void insert(int u,int v){g[++k].next=head[u];head[u]=k;g[k].to=v;} 
void pushdown(int x) 
{ 
    lazy[x*2]+=lazy[x]; 
    lazy[x*2+1]+=lazy[x]; 
    sum[x*2]=(sum[x*2]+lazy[x]*(r[x*2]-l[x*2]+1))%mod; 
    sum[x*2+1]=(sum[x*2+1]+lazy[x]*(r[x*2+1]-l[x*2+1]+1))%mod; 
    lazy[x]=0; 
} 
void pushup(int x) 
{ 
    sum[x]=sum[x*2]+sum[x*2+1]; 
} 
void add(int _l,int _r,int x,long long k) 
{ 
    if(l[x]==_l&&r[x]==_r){sum[x]=(sum[x]+(r[x]-l[x]+1)*k)%mod;lazy[x]+=k;return;} 
    pushdown(x); 
    int mid=(l[x]+r[x])/2; 
    if(_r<=mid)add(_l,_r,x*2,k); 
    else if(_l>mid)add(_l,_r,x*2+1,k); 
    else {add(_l,mid,x*2,k);add(mid+1,_r,x*2+1,k);} 
    pushup(x); 
} 
long long query(int _l,int _r,int x) 
{ 
    if(l[x]==_l&&r[x]==_r){return sum[x]%mod;} 
    pushdown(x); 
    int mid=(l[x]+r[x])/2; 
    if(_r<=mid)return query(_l,_r,x*2); 
    else if(_l>mid)return query(_l,_r,x*2+1); 
    else {return (query(_l,mid,x*2)+query(mid+1,_r,x*2+1))%mod;} 
} 
void dfs1(int u,int f,int d) 
{ 
    fa[u]=f;dep[u]=d;size[u]=1; 
    for(int i=head[u];i;i=g[i].next) 
        if(g[i].to!=f) 
        { 
            dfs1(g[i].to,u,d+1);size[u]+=size[g[i].to]; 
            if(size[g[i].to]>size[son[u]])son[u]=g[i].to; 
        } 
} 
void dfs2(int u,int tp) 
{ 
    top[u]=tp;dfs[u]=++dfsn; 
    if(son[u])dfs2(son[u],tp); 
    for(int i=head[u];i;i=g[i].next) 
        if(g[i].to!=fa[u]&&g[i].to!=son[u])dfs2(g[i].to,g[i].to); 
} 
void cz1(int x,int y,int z) 
{  
    while(top[x]!=top[y]) 
    { 
        if(dep[top[x]]>dep[top[y]]) 
        {add(dfs[top[x]],dfs[x],1,z);x=fa[top[x]];} 
        else
        {add(dfs[top[y]],dfs[y],1,z);y=fa[top[y]];} 
    } 
    if(dep[x]>dep[y])add(dfs[y],dfs[x],1,z); 
    else add(dfs[x],dfs[y],1,z); 
} 
int cz2(int x,int y) 
{ 
    long long ans=0; 
    while(top[x]!=top[y]) 
    { 
        if(dep[top[x]]>dep[top[y]]) 
        {ans=(ans+query(dfs[top[x]],dfs[x],1))%mod;x=fa[top[x]];} 
        else
        {ans=(ans+query(dfs[top[y]],dfs[y],1))%mod;y=fa[top[y]];} 
    } 
    if(dep[x]>dep[y]){ans=(ans+query(dfs[y],dfs[x],1))%mod;} 
    else {ans=(ans+query(dfs[x],dfs[y],1))%mod;} 
    return (int)ans; 
} 
void cz3(int x,int y) 
{ 
    add(dfs[x],dfs[x]+size[x]-1,1,y); 
} 
int cz4(int x) 
{ 
    return (int)query(dfs[x],dfs[x]+size[x]-1,1); 
} 
void init(int x,int _l,int _r) 
{ 
    l[x]=_l;r[x]=_r;if(_l==_r)return; 
    init(x*2,_l,(_l+_r)/2);init(x*2+1,(_l+_r)/2+1,_r); 
} 
int main() 
{ 
    int n,m,r;scanf("%d%d%d%d",&n,&m,&r,&mod);init(1,1,n); 
    for(int i=1;i<=n;i++)scanf("%d",&a[i]); 
    for(int i=1;i<n;i++) 
    { 
        int x,y;scanf("%d%d",&x,&y);insert(x,y);insert(y,x); 
    } 
    dfs1(r,r,1);dfs2(r,r); 
    for(int i=1;i<=n;i++)add(dfs[i],dfs[i],1,a[i]); 
    for(int i=1;i<=m;i++) 
    { 
        int aa,x,y,z;scanf("%d",&aa); 
        if(aa==1){scanf("%d%d%d",&x,&y,&z);cz1(x,y,z);} 
        if(aa==2){scanf("%d%d",&x,&y);printf("%d\n",cz2(x,y));}  
        if(aa==3){scanf("%d%d",&x,&y);cz3(x,y);}  
        if(aa==4){scanf("%d",&x);printf("%d\n",cz4(x));}  
    } 
    return 0; 
 }

来源：https://www.cnblogs.com/lher/p/6820977.html

标签

树链剖分

dfs

sum

top