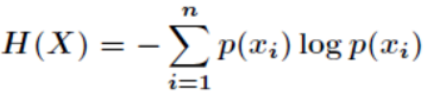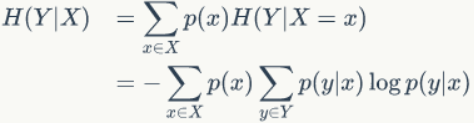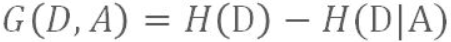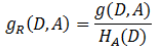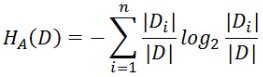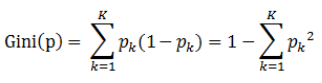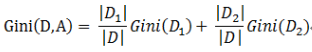条件熵:
信息熵是对观测过程中变量的不确定性的度量,基本公式为:
当X服从均匀分布时,H(x)取得最大值,这也符合感性认识。
从公式可以看出,这是一个熵值的期望,约束为随机变量X,可理解为X约束下对H(Y)的影响,因此这种信息熵被记为H(Y|X)。
信息增益:
有上述公式,感性上容易得出H(Y)大于等于H(Y|X),因为提供了X的信息,Y的熵值应该变小或者不变,因此有信息增益:
G越大,表示A提供的信息很有用,以至于H(D|A)的不确定性接近0(完全确定)
G越小,表示A提供的信息没什么用
因此可以用G来衡量变量A对D的影响,G越大越好,另外可以将A的熵值考虑到G中,有:
比如G(D,A)和G(D,B)相等,但A的熵值更小,表示A本身比较确定的情况下,对D的影响更大,因此A对D比B对D更有影响。
基尼指数:
基尼指数与信息熵类似,也是对比变量不确定性的度量,在变量A的影响下,D的基尼指数为:
这里Gini(D,A)应该是越小越好,表示在A的约束下,D的不确定变得很小。
来源:CSDN
作者:厉害了我的汤
链接:https://blog.csdn.net/YD_2016/article/details/104039251