@。Tensorflow，纯新手入门笔记->回归算法、损失函数

第七节：
机器学习中第一个算法：回归算法
亮点：
1.因变量和自变量之间的关系实现数据的预测。
2.不同自变量对因变量影响的强度。（不就是k嘛）
for example ：对房价估计时，需要确定房屋面积（自变量）与其价格（因变量）之间的关系，可以利用这一关系来预测给定面积的房屋的价格。可以有多个影响因变量的自变量。
一、线性回归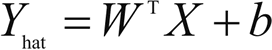
在这里插入图片描述
其中，X=(x1,x2,…,xn) 为 n 个输入变量，W=(w1,w2,…,wn) 为线性系数，b 是偏置项。目标是找到系数 W 的最佳估计，使得预测值 Y 的误差最小。
亮点：
1.W很重要，要W最佳，使得误差最小。
2.最小二乘法，可以使得W最佳。即使预测值 (Yhat) 与观测值 (Y) 之间的差的平方和最小。
3.还有个b偏置
因此，这里尽量最小化损失函数：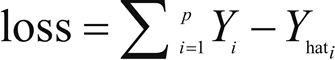
在这里插入图片描述
根据输入变量 X 的数量和类型，可划分出多种线性回归类型：
简单线性回归（一个输入变量，一个输出变量），多元线性回归（多个输入变量，一个输出变量），多变量线性回归（多个输入变量，多个输出变量）。

二、逻辑回归：用来确定一个事件的概率。通常来说，事件可被表示为类别因变量。事件的概率用 logit 函数（Sigmoid 函数）表示：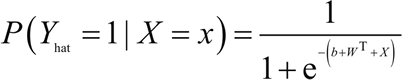
在这里插入图片描述
现在的目标是估计权重 W=(w1,w2,…,wn) 和偏置项 b。在逻辑回归中，使用最大似然估计量或随机梯度下降来估计系数。损失函数通常被定义为交叉熵项：
https://blog.csdn.net/qq_35203425/article/details/79773459 （关于交叉熵项）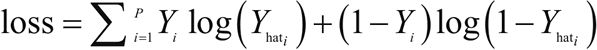
在这里插入图片描述
逻辑回归用于分类问题，例如，对于给定的医疗数据，可以使用逻辑回归判断一个人是否患有癌症。如果输出类别变量具有两个或更多个层级，则可以使用多项式逻辑回归。另一种用于两个或更多输出变量的常见技术是 OneVsAll。对于多类型逻辑回归，交叉熵损失函数被修改为：（注意，此时k是类别总数）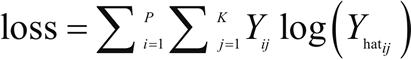
在这里插入图片描述
亮点：
1.X自变量与P（）因变量肯定要的拉！W、b也要有。
2.W也要理一理，那怎么理？就要用损失函数：交叉熵项！使用最大似然估计量或随机梯度下降来估计系数。
3.逻辑回归用于分类问题。还会存在多项逻辑回归。要是多项多类型逻辑回归，那损失函数就发生变化。

三、正则化
正则化：当有大量的输入特征时，需要正则化来确保预测模型不会太复杂。正则化可以帮助防止数据过拟合。它也可以用来获得一个凸损失函数。有两种类型的正则化——L1 和 L2 正则化，其描述如下：λ是正则化参数
L1：
当数据高度共线时，L1 正则化也可以工作。在 L1 正则化中，与所有系数的绝对值的和相关的附加惩罚项被添加到损失函数中。L1 正则化的正则化惩罚项如下：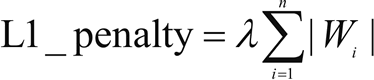
在这里插入图片描述
L2：
L2 正则化提供了稀疏的解决方案。当输入特征的数量非常大时，非常有用。在这种情况下，惩罚项是所有系数的平方之和：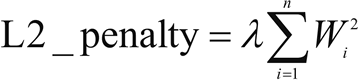

亮点：
1.正则化使你预测模型不负责，防止数据过拟合。
2.有L1,L2正则化。L1，|W| 绝对值。L2 W^2 平方。
3.λ通常在API中，需要自己调。

第八节：
损失函数：目的是找到使损失最小化的系数。
注意：
损失函数：计算的是一个样本的误差
代价函数：是整个训练集上所有样本误差的平均
目标函数：代价函数 + 正则化项

亮点：
1.声明损失函数，需要将系数定义为变量，将数据集定义为占位符。可以有一个常学习率或变化的学习率和正则化常数。

代码：

import tensorflow as tf
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

# m 是样本数量，n 是特征数量，P 是类别数量
m = 1000
n = 15
P = 2
def one():

    # Y = W*X + B
    X = tf.placeholder(tf.float32, name='X')
    Y = tf.placeholder(tf.float32, name='Y')

    # 变量初始化为0
    w0 = tf.Variable(0.0)
    w1 = tf.Variable(0.0)

    # 线性回归方程模型
    Y_hat = X * w1 + w0

    # 损失函数 tf.square()是对a里的每一个元素求平方
    loss = tf.square(Y - Y_hat, name='loss')

def two():
    # 在多元线性回归的情况下，输入变量不止一个，而输出变量仍为一个。
    # 现在可以定义占位符X的大小为 [m，n]，其中 m 是样本数量，n 是特征数量，
    X = tf.placeholder(tf.float32, name='X', shape=[m, n])
    Y = tf.placeholder(tf.float32, name='Y')

    w0 = tf.Variable(0.0)
    w1 = tf.Variable([n, 1])

    Y_hat = tf.matmul(X, w1) + w0
    # tf.reduce_mean 函数用于计算张量tensor沿着指定的数轴
    # (tensor的某一维度）上的的平均值，主要用作降维或者计算tensor（图像）的平均值。
    loss = tf.reduce_mean(tf.square(Y - Y_hat, name='loss'))

def three():
    # 在逻辑回归的情况下，损失函数定义为交叉熵。
    # 输出 Y 的维数等于训练数据集中类别的数量，其中 P 为类别数量：
    X = tf.placeholder(tf.float32, name='X', shape=[m, n])
    Y = tf.placeholder(tf.float32, name='Y', shape=[m, P])

    w0 = tf.Variable(tf.zeros([1, P]), name='bias')
    w1 = tf.Variable(tf.random_normal([n, 1]), name='weights')

    Y_hat = tf.matmul(X, w1) + w0

    # Loss tf.nn.softmax_cross_entropy_with_logits : 交叉熵函数
    entropy = tf.nn.softmax_cross_entropy_with_logits(Y_hat, Y)
    loss = tf.reduce_mean(entropy)

    lamda = tf.constant(0.8)
    # L1
    regularzation_param = lamda*tf.reduce_mean(tf.abs(w1))
    # New loss
    loss += regularzation_param

    # L2
    regularzation_param = lamda*tf.nn.l2_loss(w1)
    loss += regularzation_param