就算没有天分,只要你愿意每天花一点时间,做同样一件事情,不知不觉间,你就会走得很远。
什么是线性表?
线性表是n(n>= 0)个元素的有限序列。在表中,元素之间存在这线性的逻辑关系:
(1)表中有且仅有一个开始结点;
(2)有且仅有一个终端结点;
(3)除开始结点外,表中的每一个结点均只有一个前驱结点;
(4)除终端结点外,表中的每一个结点均只有一个后继结点;
根据他们之间的关系可以排成一个现线性序列,记作:(a1,a2,...,an)
例如:26个英文字母表(A,B,C,...,X,Y,Z)就是一个线性表
这里的ai(1<=i<=n)属于同一数据对象,具有相同的数据类型。线性表中的数据元素
个数n就是线性表的长度,称作表长,n=0时为空表。i则是数据元素ai的位序。
线性表的存储方式
线性表有两种存储方式:顺序存储和链式存储
(一)顺序表
顺序存储是在内存中用一块地址连续的存储空间按顺序存储线性表的各个数据元素。
采用顺序存储结构的性表称为顺序表,顺序表中逻辑上相邻的数据元素在物理存储位置上也是相邻的。
只要确定了存储线性表的起始位置,线性表中的任意一个数据都可随机存取:
第i个元素的地址为:Loc(ai) = Loc(a1) + size * (i - 1) 其中size是每个元素所占的空间大小。
C语言版的实现
#include <stdio.h>
#include <stdlib.h>
#define ERROR 0
#define OK 1
#define TRUE 1
#define FALSE 0
#define NOTFOUND -1
#define MAXSIZE 100
#define seqNodeDataType int
//结构体定义
typedef struct seqNode{
seqNodeDataType data[MAXSIZE];
int length;
}SeqNode;
//初始化
void Init_SeqList(SeqNode * L){
L->length = 0;
}
//判空
int IsEmpty_SeqList(SeqNode L){
if (L.length == 0) {
return TRUE;
} else {
return FALSE;
}
}
//判满
int IsFull_SeqList(SeqNode L){
if (L.length == MAXSIZE - 1) {
return TRUE;
} else {
return FALSE;
}
}
//获取真实长度
int GetListLength_SeqList(SeqNode L){
return L.length;
}
//获得index处的元素
seqNodeDataType GetElem_SeqList(SeqNode L, int index){
if (index < 0 || index >= L.length) {
return ERROR;
}
return L.data[index];
}
//按值查找
int IndexOf_SeqList(SeqNode L, seqNodeDataType elem){
for (int i = 0; i < L.length; ++i) {
if (L.data[i] == elem) {
return i;
}
}
return NOTFOUND;
}
//打印输出
void Print_SeqList(SeqNode L){
printf("[");
for (int i = 0; i < L.length; ++i) {
if (i == L.length - 1) {
printf("%d", L.data[i]);
} else {
printf("%d,", L.data[i]);
}
}
printf("]\n");
}
//在index处插入元素
int InsertOfIndex_SeqList(SeqNode *L, int index, seqNodeDataType elem){
if (index < 0 || index > L->length) {
return ERROR;
}
if (IsFull_SeqList(*L)) {
return ERROR;
}
for (int i = L->length; i > index; --i) {
L->data[i] = L->data[i - 1];
}
L->data[index] = elem;
L->length++;
return OK;
}
//首部添加元素
int InsertFirst_SeqList(SeqNode *L, seqNodeDataType elem){
InsertOfIndex_SeqList(L, 0, elem);
}
//尾部添加元素
int InsertLast_SeqList(SeqNode *L, seqNodeDataType elem){
InsertOfIndex_SeqList(L, L->length, elem);
}
//删除元素
int DeleteOfIndex_SeqList(SeqNode *L, int index, seqNodeDataType *result){
if (index < 0 || index > L->length) {
return ERROR;
}
if (IsEmpty_SeqList(*L)) {
return ERROR;
}
for (int i = index; i < L->length - 1; ++i) {
L->data[i] = L->data[i + 1];
}
L->length--;
return OK;
}
//清空数据
int Clear_SeqList(SeqNode *L){
L->length = 0;
return OK;
}
缺点在哪里
由于顺序表底层实现是一个数组,而数组的容量无法改变,因而存在的最大问题就是空间分配多大才合适呢?
过小导致数据无法继续存放,而过大则造成空间的浪费。可以使用高级语言来优化顺序表,实现动态数组扩容。
Java版实现
package cn.boom.list;
public class SeqList<T> {
private T[] data;
private int size;
//无参构造
public SeqList(){
data = (T[]) new Object[10];
size = 0;
}
//带参构造 :参数 容量
public SeqList(int capacity) {
data = (T[]) new Object[capacity];
size = 0;
}
/**
* 获取真实长度(数据个数)
* @return size
*/
public int getSize(){
return this.size;
}
/**
* 获取index索引位置的元素
* @param index
* @return data[index]
* @throws IllegalArgumentException 参数不合法异常
*/
public T getIndexOf(int index) throws IllegalArgumentException{
//参数合法性校验
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Illegal Index !");
}
return this.data[index];
}
//修改值
public void set(int index, T elem) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Illegal Index !");
}
data[index] = elem;
}
/**
* 按值查找 返回elem第一次出现的下标 未找到返回-1
* @param elem
* @return index
*/
public int locationElem(T elem){
for (int i = 0; i < this.size; i++) {
if (elem.equals(this.data[i])) {
return i;
}
}
return -1;
}
//是否存在元素
public boolean contains(T elem){
return locationElem(elem) != -1;
}
//表是否为空
public boolean isEmpty(){
return (size == 0);
}
//表是否为空
public boolean isFull(){
return (size == data.length);
}
//获取容量
public int getCapacity(){
return data.length;
}
//在 index处插入一个元素
public void add(int index, T elem) {
//参数合法性校验
if (index < 0 || index > size) {
throw new IllegalArgumentException("Illegal Index ! index is " + index);
}
if (isFull()) {
updateCapacity(data.length * 2);
}
//在 index 后的数据后移
for (int i = size; i > index; i--) {
this.data[i] = this.data[i - 1];
}
this.data[index] = elem;
size++;
}
//在数组首部添加元素
public void addFirst(T elem) {
add(0, elem);
}
//在数组尾部添加元素
public void addLast( T elem){
add(this.size,elem);
}
//更新数组容量
public void updateCapacity(int newCapacity) {
T[] newArray = (T[]) new Object[newCapacity];
for (int i = 0; i < size; i++) { // copy原数组中的数据
newArray[i] = data[i];
}
this.data = newArray;
}
//删除下标为index的元素并返回
public T remove(int index){
if (index < 0 || index > size) {
throw new IllegalArgumentException("Illegal Index ! index is " + index);
}
T elem = data[index];
for (int i = index; i < size - 1; i++) {
data[i] = data[i + 1];
}
size--;
if (size < data.length / 2) { //缩容
updateCapacity(data.length / 2);
}
return elem;
}
//删除第一个元素
public T removeFirst() {
return remove(0);
}
//删除最后一个元素
public T removeLast() {
return remove(size - 1);
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append("SeqList{");
res.append(" data=[");
for (int i = 0; i < this.size; i++) {
res.append(this.data[i].toString());
if (i != size - 1) {
res.append(',');
}
}
res.append("], size=" + size + ", capacity=" + getCapacity() + " }");
return res.toString();
}
}
以上的代码虽然实现了数组空间的动态扩容和缩容,但顺序表依然是一种非动态的存储结构。
下面介绍动态存储结构的链表。
(二)单链表
链表是通过一组任意的存储单元来存储线性表中的数据元素。这组存储单元可以是连续的,也可以是不连续的。
为建立起数据元素之间的线性关系,对于每个数据元素an,除了存放数据元素自身的信息外,还必须有包含指示该元素直接后继元素存储位置的信息,
这两部分信息组成个“结点”,即每个结点都至少包括两个域,一个域存储数据 元素信息,称为数据域;另一个域存储直接后继元素的地址,称为指针域。

有时为了操作方便,在单链表的第一个结点之前附加一 个结点, 称为头结点。头结点的数据域可以存储标题、表长等信息,也可以不存储任何信息,其指针域存储第个结点的首地址, 头结点由头指针指向。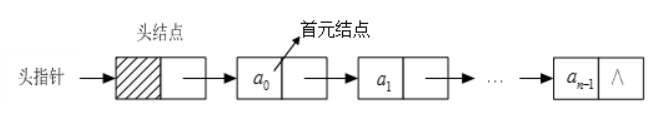
单链表C语言版
#include <stdio.h>
#include <stdlib.h>
#define ERROR 0
#define OK 1
#define TRUE 1
#define FALSE 0
#define NOTFOUND -1
#define linkedListDataType int
typedef struct linkedNode{
linkedListDataType data;
struct linkedNode* next;
}LNode;
//头插法建立单链表
int CreateHead_LinkedList(LNode ** H){
(*H)->next = NULL;
int elem;
scanf("%d",&elem);
while (elem != -1) {
LNode* s = (LNode *) malloc(sizeof(LNode));
s->data = elem;
s->next = (*H)->next;
(*H)->next = s;
scanf("%d", &elem);
}
return OK;
}
//初始化链表
LNode *Init_LinkedList() {
LNode *H = (LNode *) malloc(sizeof(LNode));
if (H == NULL) {
return ERROR;
}
H->next = NULL;
return H;
}
//尾插法建立单链表
int CreateTail_LinkedList(LNode ** H){
(*H)->next = NULL;
LNode *p = *H;
int elem;
scanf("%d",&elem);
while (elem != -1) {
LNode* s = (LNode *) malloc(sizeof(LNode));
s->data = elem;
s->next = NULL;
p->next = s;
p = s;
scanf("%d", &elem);
}
}
//获取链表长度
int GetSize_LinkedList(LNode *H){
LNode *p = H;
int size = 0;
while (p->next != NULL) {
size++;
p = p->next;
}
return size;
}
//判断链表是否为空
int IsEmpty(LNode *H){
if ( H == NULL || GetSize_LinkedList(H) == 0) {
return 1;
}
return 0;
}
//输出打印链表
void Print_LinkedList(LNode *H){
LNode *p = H;
printf("head -> ");
while (p->next != NULL) {
printf("%d -> ", p->next->data);
p = p->next;
}
printf("NULL\n");
}
//获取索引结点
LNode* GetNode_LinkedList(LNode *H, int index) {
if (index == -1) {
return H;
}
LNode *p = H;
int count = 0;
while (p->next != NULL) {
p = p->next;
if (index == count) {
return p;
}
count++;
}
return NULL;
}
//通过索引删除结点
int DeleteNodeByIndex_LinkedList(LNode *H, int index) {
LNode *p = GetNode_LinkedList(H, index - 1);
LNode *q = p->next;
p->next = p->next->next;
free(q);
return OK;
}
//在索引处插入一个结点
int InsertNodeIndexOf_LinkedList(LNode *H, int index, linkedListDataType elem) {
if (index > GetSize_LinkedList(H)) {
return ERROR;
}
LNode *p = GetNode_LinkedList(H, index - 1);
LNode* s = (LNode *) malloc(sizeof(LNode));
if (s == NULL) {
return ERROR;
}
s->data = elem;
s->next = p->next;
p->next = s;
return OK;
}
//在链表尾部插入一个元素
int InsertNodeTail_LinkedList(LNode *H, linkedListDataType elem) {
InsertNodeIndexOf_LinkedList(H,GetSize_LinkedList(H),elem);
return OK;
}
//修改索引处结点的值
int UpdateNodeByIndex_LinkedList(LNode *H, int index, linkedListDataType elem){
LNode *p = GetNode_LinkedList(H, index);
p->data = elem;
return OK;
}
//删除重复元素结点
void DeleteRepeatElem(LNode *H){
if (H == NULL) {
return;
}
LNode *p = H->next;
if (p == NULL) {
return;
}
while (p->next != NULL) {
LNode *q = p->next;
while (q != NULL) {
if (p->data == q->data) {
//删除q结点
LNode *t = q;
q = q->next;
free(t);
p->next = q;
} else {
q = q->next;
}
}
p = p->next;
}
}
Java实现单链表
package cn.boom.list;
public class LinkedList<T> {
private Node head;//虚拟头结点
private int size;//表长
private class Node {
private T data;
private Node next;
public Node() {
this.data = null;
this.next = null;
}
public Node(T data) {
this.data = data;
this.next = null;
}
public Node(T data, Node node) {
this.data = data;
this.next = node;
}
}
public LinkedList() {
this.head = new Node();
this.size = 0;
}
/**
* 获取链表长度
* @return
*/
public int getSize() {
return this.size;
}
/**
* 判断链表是否为空
* @return
*/
public boolean isEmpty() {
return size == 0;
}
/**
* 在链表的index(0-size)位置添加新的元素
* @param index
* @param elem
*/
public void add(int index, T elem) {
if (index < 0 || index > size) {
throw new IllegalArgumentException("Index Is Illegal Argument ! index = " + index);
}
Node node = this.head;
for (int i = 0; i < index ; i++) { //找到待插入下标的前一个结点
node = node.next;
}
Node e = new Node(elem);
//插入结点
e.next = node.next;
node.next = e;
this.size++;
}
/**
* 在链表首部位置添加新的元素
* @param elem
*/
public void addFirst(T elem) {
add(0,elem);
}
/**
* 在链表尾部位置添加新的元素
* @param elem
*/
public void addLast(T elem) {
add(size,elem);
}
/**
* 获得链表的第index(0-size)个位置的元素
* @param index
* @return
*/
public T get(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Index Is Illegal Argument ! index = " + index);
}
Node node = this.head.next;
for (int i = 0; i < index; i++) {
node = node.next;
}
return node.data;
}
/**
* 修改链表的第index(0-size)个位置的元素
* @param index
* @param elem
*/
public void set(int index, T elem) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Index Is Illegal Argument ! index = " + index);
}
Node node = this.head.next;
for (int i = 0; i < index; i++) {
node = node.next;
}
node.data = elem;
}
/**
* 查询表中是否包含该元素
* @param elem
* @return
*/
public boolean contains(T elem) {
Node node = this.head.next;
while (node != null) {
if (node.data.equals(elem)) {
return true;
}
node = node.next;
}
return false;
}
/**
* 删除index(0-size)处的结点并返回数据
* @param index
* @return
*/
public T remove(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Index Is Illegal Argument ! index = " + index);
}
Node node = this.head.next;
for (int i = 0; i < index - 1; i++) { //找到要删除节点的前一个结点
node = node.next;
}
Node s = node.next;
node.next = s.next;
s.next = null;
this.size--;
return s.data;
}
/**
* 从表中删除元素e
* @param elem
*/
public void removeElement(T elem) {
Node preNode = this.head;
Node node = preNode.next;
while (node != null) {
if (node.data.equals(elem)) {
preNode.next = node.next;
node.next = null;
node = preNode.next;
this.size--;
continue;
}
preNode = node;
node = node.next;
}
}
@Override
public String toString() {
Node node = this.head.next;
StringBuilder res = new StringBuilder();
res.append("head -> ");
for (int i = 0; i < this.size; i++) {
res.append(node.data.toString() + " -> ");
node = node.next;
}
res.append("NULL");
return res.toString();
}
}
顺序表和链表的优缺点
顺序表优点:
(1)用数组存储数据元素,操作方法简单,容易实现。
(2)无须为表示结点间的逻辑关系而增加额外的存储开销。
(3)存储密度高。
(4)顺序表可按元素位序随机存取结点。
缺点:
(1)做插入、删除操作时,须大量地移动数据元素,效率比较低。
(2)要占用连续的存储空间,存储分配只能预先进行。如果估计过大,可能导致后部大量空闲置;如果预先分配过小,又会造成数据溢出。
链表的优缺点刚好和顺序表相反。
参考文献
[1]王曙燕.数据结构与算法:人民邮电出版社
来源:CSDN
作者:白日梦想家
链接:https://blog.csdn.net/qq_42080839/article/details/103969621