[常用排序算法] 希尔排序 （Shell Sort）

一 基本思想

希尔排序是希尔（Donald Shell）于1959年提出的一种排序算法。希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序，同时该算法是冲破O(n2)的第一批算法之一。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

希尔排序是把元素按下表的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个数组被分成一组，算法便终止。

二 算法描述

来看下希尔排序的基本步骤，在此我们选择增量 gap = length / 2，缩小增量继续以 gap = gap / 2 的方式，这种增量选择我们可以用一个序列来表示，{n / 2, (n / 2) / 2 … 1}，称为增量序列。希尔排序的增量序列的选择与证明是个数学难题，我们选择的这个增量序列是比较常用的，也是希尔建议的增量，称为希尔增量，但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。

先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，具体算法描述：

选择一个增量序列 t1，t2，…，tk，其中 ti > tj，tk = 1；
按增量序列个数 k，对序列进行 k 趟排序；
每趟排序，根据对应的增量ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

三 动图演示

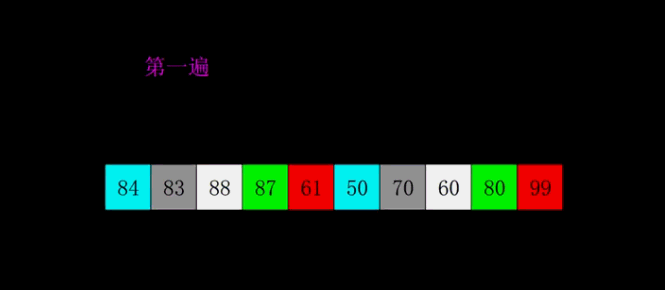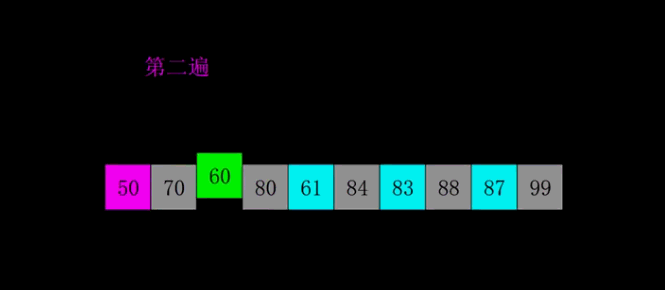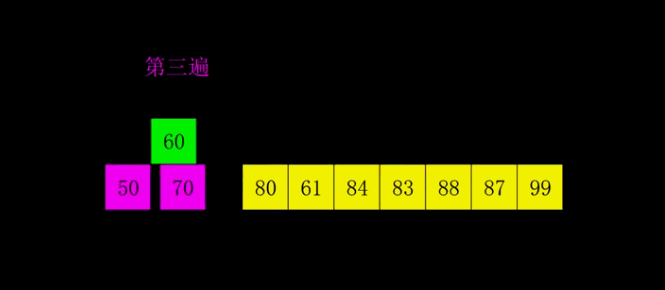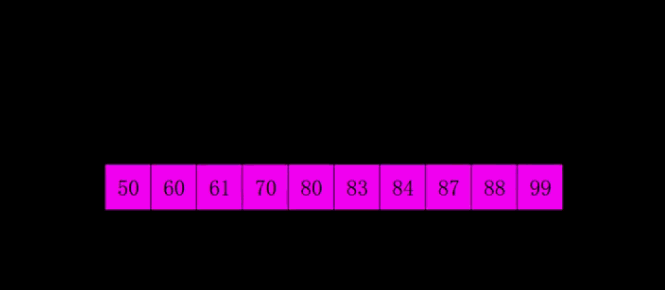
四 代码实现

public class ShellSort {
    public static void main(String[] args){
        int[] arr = {2, 4, 11, 0, -4, 333, 90};
        printArr(arr);
        xeSort(arr);
        printArr(arr);
    }
    public static void xeSort(int[] arr){
        int len = arr.length;
        //定义希尔变量
        int temp, gap = len/2;
        //间隔gap缩小到0的时候就退出循环
        while(gap > 0){
            //每组进行直接插入排序
            for(int i = gap; i<len; i++){
                //i 代表待插入元素的索引
                temp = arr[i];
                //preIndex 代表i 的上一个元素，相差一个增量gap
                int preIndex = i- gap;
                //preIndex < 0 时退出循环，说明j时最小的元素的索引值
                //或者是arr[preIndex] > temp时退出循环，说明preIndex 是比temp小的元素的索引值
                while(preIndex >= 0 && arr[preIndex] > temp){
                    //把元素往后挪
                    arr[preIndex + gap] = arr[preIndex];
                    preIndex -= gap;
                }
                arr[preIndex + gap] = temp;
            }
            //缩小增量
            gap /= 2;
        }

    }

    public static void printArr(int[] arr){
        for(int i = 0; i<arr.length;i++){
            if(i==0){
                System.out.print("["+arr[i]+",");
            }else if(i == arr.length - 1){
                System.out.print(arr[i]+"]");
            }else {
                System.out.print(arr[i]+",");
            }
        }
        System.out.println("");
    }
}

五 复杂度分析

时间复杂度：O(nlogn)
空间复杂度：O(1)
稳定性：不稳定

参考链接 https://blog.csdn.net/YelloJesse/article/details/90724105

来源：CSDN

作者：你看这人，真菜

链接：https://blog.csdn.net/qq_43584847/article/details/103692946