Unsupervised Feature Learning via Non-Parametric Instance Discrimination

论文地址：Unsupervised Feature Learning via Non-Parametric Instance Discrimination
github代码:NCE代码

摘要:

在有标签数据上训练的神经网络分类器能够很好的捕捉图片间的视觉相似性。文章假设：我们能通过训练基于实例（将每一个样本视为单独的类别）的分类器代替基于类别的分类器，得到可以捕捉视觉相似性的特征表达。我们将其总结为非参数化实例级判别，并且通过**噪声对比估计（noise-contrastive estimation）**解决大量实例类别引起的计算困难。
我们的实验证明了，在无监督学习的限制下，我们的方法在ImageNet数据集上超越了当前最好方法。采用更多的训练数据和更先进的网络结构，我们的方法能够进一步提高分类准确率。通过微调学习到的特征，我们能观察到与半监督学习和目标检测任务上相当的结果。同时，我们的非参数化模型十分紧致：每张图片仅需要提取128维的特征，百万量级的图片也仅需要600MB存储空间，使得实际运行时能够很快达成近邻检索的目的。

引言

研究者在本文中提出的无监督学习的创新方法源于对监督学习物体识别结果的一些观察。在 ImageNet 上，top-5 分类误差远低于 top-1 误差 ，并且图像在 softmax 层输出中的预测值排第二的响应类更可能与真实类有视觉关联。

如图 1 所示，包含猎豹（leopard）的图像被识别成美洲豹（jaguar）的概率比识别成书柜（bookcase）高很多 [11]。这一观察表明，经典的判别式学习方法在没有干预时可以自动发现语义类别之间的表面（明显的）相似性。换句话说，明显的相似性不是来自语义注释，而是来自图像本身。

图 1：激励研究者提出无监督方法的有监督学习效果图。以猎豹图片为例，网络输出的几个最高响应类都是视觉相关的，例如美洲豹和猎豹。数据本身的表面相似性而非语义标签，使得某些类比其他类更加接近。该无监督方法将类监督发展到极致，并学习了辨别各个单独实例的特征表示。

然而，我们也面临着一个重大的挑战，因为现在“类”的数量是整个训练集的大小。对于ImageNet来说，它将是120万个类，而不是1000个类(因为是以每个图像为一个实例类,所以是120万个类别,而不是1000个类别).简单地将softmax扩展到更多的类是不可行的。研究者通过使用噪声对比估计（NCE）[9] 逼近的 softmax 分布并采用近端正则化方法 [29] 以稳定训练过程来解决这个问题。

为了评估无监督学习的有效性，过去的工作如 [2,31] 依赖于线性分类器（例如，支持向量机（SVM）），在测试时将学习到的特征与类别信息结合以便进行分类。但是，我们不清楚未知的测试任务为什么可以将训练学习到的特征线性分离。

作者提倡对训练和测试采用非参数方法。他们将实例级别的分类看作度量学习问题，其中实例之间的距离（相似度）是以非参数方式直接从特征中计算得到的。也就是说，每个实例的特征都存储在离散的内存块中，而不是网络中的权重。

在测试阶段，使用基于学习度量的 k-近邻（kNN）进行分类。因为模型的学习和评估都与图像间的相同的度量空间有关，所以其训练和测试是一致的。研究者总结了与 SVM 和 kNN 的准确率对比实验结果。

实验结果表明，在无监督领域，该方法在图像分类方面远超过最先进的方法。具体地，在 ImageNet 1K [1] 上的 top-1 准确率为 46.5％，Places 205 [41] 为 41.6％。若有更多的训练数据和更好的网络架构，该算法会持续提高测试结果。

通过微调学习到的特征，可进一步获得半监督学习和物体检测任务的具竞争性的结果。最后，该非参数化模型非常紧凑：每张图片有 128 个特征，存储一百万张图像仅需 600MB，从而在运行时实现快速最近邻检索。

图 2：本文提出的无监督特征学习方法的工作流图。研究者使用骨干 CNN 将每个图像编码为 128 维空间并进行 L2 归一化的特征向量。最佳特征嵌入过程是通过实例级判别器学习的，该判别器尝试将训练样本的特征最大程度地散布在 128 维的单位球上。

近期工作

近期关于无监督学习的工作主要可以分为两类：生成式模型和自监督模型。
Generative Modes
生成式模型的出发点在于尽可能重构数据的分布，典型的方法有受限玻尔兹曼机（RBM），自编码器（Autoencoders）。生成式模型得到的隐空间特征能够有效帮助分类，近期的生成式模型有生成对抗网络（GAN）和变分自编码器（VAE）
Self-supervised Learning
自监督模型利用内部数据结构，通过预测图片来训练模型。具体地，模型需要预测给定实例缺失的部分。为了学习图像的表达，预测任务可以分为上下文预测，目标计数，填补图像缺失部分，将灰度图像恢复成彩色图像，甚至是完成拼图游戏。对于视频，自监督模型包括：跟踪时间连续性，预测未来帧图像，或者保持自我运动的轨迹。
Metric Learning
每个特征表示F在实例x和y之间引入一个度量:dF(x, y) = ||F(x) -F(y)||,因此，特征学习也可以看作是度量学习的一种特定形式。已有大量关于度量学习的研究。度量学习的成功应用通常会带来有竞争力的表现，例如在人脸识别[35]和person Re-Id[46]上。在这些任务中，测试时的类别与训练时的类别是分离的。一旦一个网络被训练，只能从它的特征表征来推断，而不能从随后的线性分类器来推断。度量学习已被证明对few-shot是有效的[38,41,37]。人脸识别度量学习的一个重要技术点是归一化[35,22,43]，我们在这项工作中也利用了这一点。注意，这里提到的所有方法都需要以某种方式进行监督。我们的工作是完全不同的:它以一种无监督的方式学习特性，从而获得度量.
Exemplar CNN
Exemplar CNN[5]与我们的工作类似。基本的区别在于，它在训练和测试中都采用了参数的范式，而我们的方法本质上是非参数的。我们在第4.1节的实验中研究了这种差别。举例来说，Exemplar CNN在是在大规模的数据集上计算的，比如ImageNet。

3. Approach

我们的目标是无需监督信息学习一个特征映射：v = f_θ(x), f_θ是以θ为参数的卷积神经网络，将图片x映射成特征v。映射同样包含了图像空间的度量d_θ(x,y)=∣∣f_θ(x)−f_θ(y)∣∣对于实例x和y.一个好的映射应该能够将视觉相似的图片投影得相近。我们的无监督特征学习是实例级别的判别式学习，我们将每张图片都当作一个独特的类别对待并训练一个分类器将这些类别分开.
3.1. Non-Parametric Softmax Classifie
Parametric Classifier
我们使用softmax标准制定实例级分类目标,假如我们有n个图像$x_{1}$,$x_{2}$…,$x_{n}$和他们的特征$v_{1}$,$v_{2}$…$v_{n}$,对应关系是$v_{i}=f_{\theta}(x_{i})$,在传统的softmax公式中,图像x对应特征$v=f_{\theta}(x)$.它被当作第ii张图片的概率是
$P(i | v)=\frac{\exp \left(w_{i}^{T} v\right)}{\sum_{j=1}^{n} \exp\left(w_{j}^{T} v\right)}$

w_j是j类的权重向量，$\mathbf{w}_{j}^{T} \mathbf{v}$衡量着v与第j类的匹配程度.
假设特征维度是128，图片数目为120万，这一层的参数数目超过15亿。
Non-Parametric Classifier
式(1)中的参数softmax公式的问题是，权向量w作为一个类原型，妨碍了实例之间的比较。
研究者们提出了非参数的公式:用$\mathbf{v}_{j}^{T} \mathbf{v}$取代$\mathbf{w}_{j}^{T} \mathbf{v}$,并且通过L2正则化使得$\|\mathbf{v}\|=1$,然后概率公式$P(i | \mathbf{v})$为:
$P(i | \mathbf{v})=\frac{\exp \left(\mathbf{v}_{i}^{T} \mathbf{v} / \tau\right)}{\sum_{j=1}^{n} \exp \left(\mathbf{v}_{j}^{T} \mathbf{v} / \tau\right)}$
,这里比较的是$\mathbf{V}_{i}^{\frac{T}{}}$和$\mathbf{V}$之间的匹配程序.
τ是个温度参数控制分布的集中程度。学习的目标是最大化联合概率密度$\prod_{i=1}^{n} P_{\theta}\left(i | f_{\theta}\left(x_{i}\right)\right)$,等价于最小化$J(\theta)=-\sum_{i=1}^{n} \log P\left(i | f_{\theta}\left(x_{i}\right)\right)$
Learning with A Memory Bank
为了计算Eq.(2)中的概率P(i|v)，需要对所有的图像使用{v_j}。我们保留了一个用于存储[46]的特征{v_j}的memory bank V，而不是每次都对这些特征进行详尽的计算。在接下来的文章中，我们将介绍memory bank的独立设置和特征在网络中的前向传播。让$V=\left\{\mathbf{v}_{j}\right\}$是memory bank和$\mathbf{f}_{i}=f_{\boldsymbol{\theta}}\left(x_{i}\right)$是Xi的特征。在每个迭代通过随机梯度下降优化学习特征fi以及网络参数θ。然后$\boldsymbol{f}_{i}$在其相对应的实例下去更新V,我们初始化memory bank V中的特征为随机的单元向量.
3.2. Noise-Contrastive Estimation Computing
在公式(2)中，当类n的数量非常大时，例如在数百万的规模下，计算非参数softmax的成本是令人望而却步的。但是类似的问题在学习单词嵌入的文献中也得到了很好的解决[25,24]，其中单词的数量也可以扩展到数百万。降低计算复杂度的常用技术有层次化softmax（hierarchical softmax），噪声对比估计（noise-contrastive estimation）和副采样（negative sampling）。
我们采用NCE来近似完整的softmax分布，为了解决计算训练集中所有实例的相似度的困难。研究人员将多分类任务转化为一系列二分类任务，二分类任务是判断样本是来自于真实数据还是噪声数据。特别的，在我们的模型中，特征表示V对应于第i个实例的概率为:
$\begin{aligned} P(i | \mathbf{v}) &=\frac{\exp \left(\mathbf{v}^{T} \mathbf{f}_{i} / \tau\right)}{Z_{i}} \\ Z_{i}=& \sum_{j=1}^{n} \exp \left(\mathbf{v}_{j}^{T} \mathbf{f}_{i} / \tau\right) \end{aligned}$
这里的$Z_{i}$是一个常量.我们将噪声分布视为均匀分布：$P_{n}=1 / n$，并且假设噪声样本为真实样本的m倍，样本i来自与真实样本分布的概率为：$h(i, \mathbf{v}):=P(D=1 | i, \mathbf{v})=\frac{P(i | \mathbf{v})}{P(i | \mathbf{v})+m P_{n}(i)}$
我们近似的训练目标是最小化数据和噪声样本的负对数后验分布:$J_{N C E}(\theta)=-E_{P_{d}}[\operatorname{logh}(i, v)]-m E_{P_{n}}\left[\log \left(1-h\left(i, v^{\prime}\right)\right)\right]$
$P_{d}$表示实际数据分布,对于$P_{d}$而言,v是于$x_{i}$的相连的特征,然而对于$P_{n}$而言,$\mathbf{v}^{\prime}$是另外一个图像的特征,根据噪声分布$P_{n}$随机采样.在我们的模型中，v和$\mathbf{v}^{\prime}$从非参数memory bank V中采样。

计算归一化常数$Z_{i}$是耗时的，我们将其视为常数，并通过蒙特卡洛近似它：$Z \approx Z_{i} \approx n E_{j}\left[\exp \left(v_{j}^{T} f_{i} / \tau\right)\right]=\frac{n}{m} \sum_{k=1}^{m} \exp \left(v_{j k}^{T} f_{i} / \tau\right)$
在这,{$j_{k}$}是索引的随机子集,根据经验，我们发现从初始批次导出的近似在实践中是有效的。
NCE将每个样本的计算复杂度从O(n)降低到O(1)。经过如此大幅度的减小，我们的模型仍然具有竞争力.
3.3. Proximal Regularization
与典型的分类每个类有多个实例不同，我的每个类只有一个实例.在每个训练epoch中，每类样本仅出现一次，训练过程由于随机采样的波动而震荡，我们采取如下的正则项保证训练过程的稳定,在当前迭代t,$x_{i}$的的特征表示为:$\mathbf{v}_{i}^{(t)}=f_{\boldsymbol{\theta}}\left(x_{i}\right)$,memory bank中保存着前一次迭代的特征$V=\left\{\mathbf{v}^{(t-1)}\right\}$,$P_{d}$中的正样本的损失函数为:$-\log h\left(i, \mathbf{v}_{i}^{(t-1)}\right)+\lambda\left\|\mathbf{v}_{i}^{(t)}-\mathbf{v}_{i}^{(t-1)}\right\|_{2}^{2}$
$\lambda\left\|\mathbf{v}_{i}^{(t)}-\mathbf{v}_{i}^{(t-1)}\right\|_{2}^{2}$部分为正则项,去保证训练过程的稳定.当学习收敛时，迭代之间的差异$\mathbf{v}_{i}^{(t)}-\mathbf{v}_{i}^{(t-1)}$逐渐消失，增加的损失减少到原来的损失。随着训练收敛，两次迭代过程中的特征差异也随之减少，最终的损失函数为：:$\begin{aligned} J_{N C E}(\boldsymbol{\theta}) &=-E_{P_{d}}\left[\log h\left(i, \mathbf{v}_{i}^{(t-1)}\right)-\lambda\left\|\mathbf{v}_{i}^{(t)}-\mathbf{v}_{i}^{(t-1)}\right\|_{2}^{2}\right] \\ &-m \cdot E_{P_{n}}\left[\log \left(1-h\left(i, \mathbf{v}^{(t-1)}\right)\right)\right] \end{aligned}$从图3可以看出，从经验上看，近似正则化有助于稳定训练，加速收敛，改善学习表示，而额外成本可以忽略不计。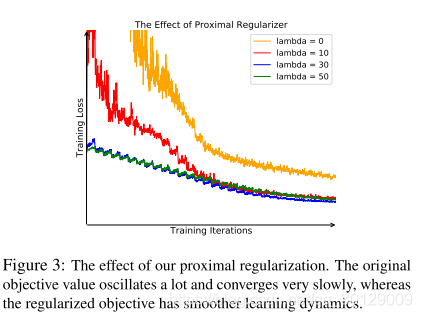

3.4. Weighted k-Nearest Neighbor Classifier
去分类测试图像$\hat{x}$,我们首先计算其特性$\hat{\mathbf{f}}=$$f_{\theta}(\hat{x})$,然后比较它和在memory bank中的嵌入图像,使用余弦相似性$s_{i}=\cos \left(\mathbf{v}_{i}, \hat{\mathbf{f}}\right)$,k个最近邻，用$N_{k}$表示，然后通过加权投票进行预测。特别的，类c将会获得总的权值$w_{c}=\sum_{i \in \mathcal{N}_{k}} \alpha_{i} \cdot 1\left(c_{i}=c\right)$, 邻居$x_{i}$的权值取决于相似度$\alpha_{i}=\exp \left(s_{i} / \tau\right)$。在训练中,我们选择τ= 0.07,k = 200.

4. Experiments

我们进行了四组不同的实验，第一个实验在CIFAR-10数据上比较了non-parametric softmax和parametric softmax的性能，第二组实验在ImageNet数据集上比较了各种无监督学习方法的性能。最后两组实验调查了两组不同的实验，半监督学习和目标检测，证明了我们方法学习到的特征具有良好的泛化能力。
**4.1. Parametric vs. Non-parametric Softmax **
本文的一个关键的新颖性是非参数的softmax分类。与传统的参数型 softmax相比，我们的softmax允许非参数的度量转移到监督任务上。我们比较了CIFAR-10[17]上的参数化和非参数化形式，这是一个包含10个类中的50,000个训练实例的数据集。这个大小允许我们在不使用任何近似的情况下计算式(2)中的非参数的softmax。我们使用ResNet18作为骨干网络，其输出特征映射到128维向量.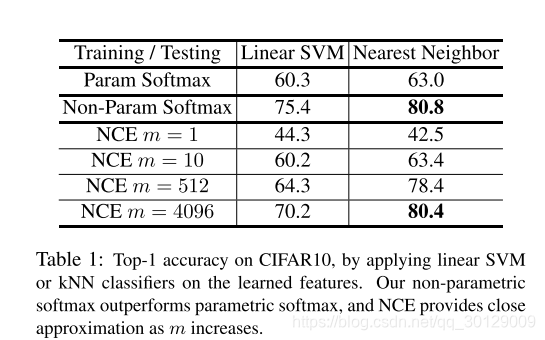

表 1：通过在学习到的特征上应用线性 SVM 或 kNN 分类器在 CIFAR10 的 Top-1 准确率。本文提出的非参数化的 softmax 优于参数化的 softmax，并且用 NCE 方法 得到的准确率随 m 单调递增。

我们评估了基于学习特征表示的分类有效性。A common practice [48, 2, 31] is to train an SVM on the learned feature over the training set，然后根据训练网络中提取的特征对测试实例进行分类。此外，我们还使用最近邻分类器来评估所学习的特征。后者直接依赖于特征度量，可以更好地反映表示特征的质量.
表1显示了CIFAR10上top-1的分类精度。在参数化softmax下学习的特征的基础上,我们获得了线性SVM分类准确率分别为60.3%和和kNN分类准确率为63.0%在非参数softmax的特征学习上，线性SVM和最近邻分类器的准确率分别提高到75.4%和80.8%，而最近邻分类器的准确率提高了18%.
我们还研究了NCE非参数近似值softmax的质量(第3.2节)。近似值由m控制，m是为每一种情况分类错误的数目。当m = 1时，kNN的准确率显著下降至42.5%。当m增加，性能稳步提升。当m = 4,096时，精度接近于m = 49999 ,不含任何近似的全形式评价。这一结果为NCE是一种有效的近似提供了保证。
4.2. Image Classification
我们学习了ImageNet ILSVRC上的特征表示,并与典型的无监督学习方法进行了比较.
实验设置:研究者通过经验验证来选择并设计参数。具体来说，他们设定 τ= 0.07，并使用 m = 4,096 的 NCE 来平衡性能和计算成本。该模型使用带 momentum 的 SGD 训练 200 个 epoch。批量大小为 256，学习率初始化为 0.03，在训练 120 个 epoch 后每 40 个 epoch 乘一次 0.1。
对比实验 :研究者将他们的方法与随机初始化的网络（作为下界）及各种无监督学习方法进行了比较，包括自监督学习 [2,47,27,48]、对抗学习 [4] 和 Exemplar CNN [3]。split-brain 自编码器 [48] 提供代表当前最佳水平的强大基线。
在他们的初版论文中，他们的实验网络都基于 AlexNet 架构 [18]，除了 exemplar CNN [5]，其基于 ResNet-101 [3]。由于网络架构对性能有很大影响，研究者考虑了一些经典的架构：AlexNet [18]、VGG16 [36]、ResNet-18 和 ResNet-50 [10]。
研究者使用两种不同的标准评估性能：（1）对从 conv1 到 conv5 的中间特征运行线性 SVM。注意，VGG16 和 ResNet 中也有对应层 [36,10]。（2）对输出特征运行 kNN。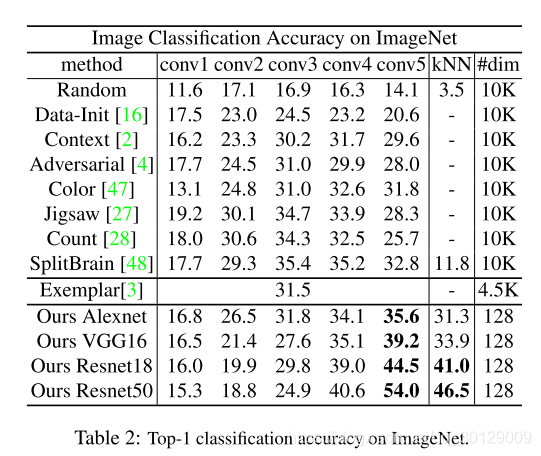

表 2：在 ImageNet 上的 Top-1 分类准确率。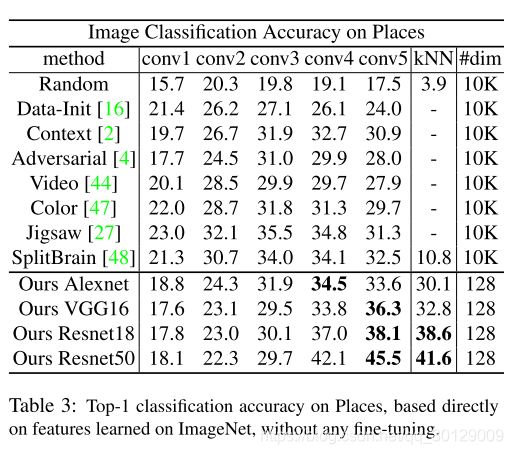

表 3：直接基于在 ImageNet 上学习特征的、没有微调的在 Places 上的 Top-1 分类准确率。
Feature generalization
我们还研究了如何将学习到的特征表示推广到其他数据集。在相同的设置下，我们对场景分类的大数据集[49]进行了另一次大规模的实验，该数据集包含205个类别的2.45M训练图像。在这个实验中，我们直接使用在ImageNet上训练的特征提取网络，而不进行细化。表3比较了不同方式和不同评价策略下的结果。再次，使用基于conv5特征的线性分类器，我们的方法在AlexNet和ResNet-50中分别实现了top-1的34.5%和45.5%的具有竞争力的表现。，我们用ResNet- 50实现了41.6%的准确率。结果表明，该方法具有较强的泛化能力。
训练和测试目标的一致性
非监督特征学习是困难的，因为训练目标与测试目标是不可知的。良好的训练目标应体现在测试表现上持续提高。我们研究了训练损失与测试精度之间的关系。图4显示，随着训练的进行，我们的测试精度不断提高，没有出现过拟合的迹象。进一步优化训练目标，可以进一步提高测试精度.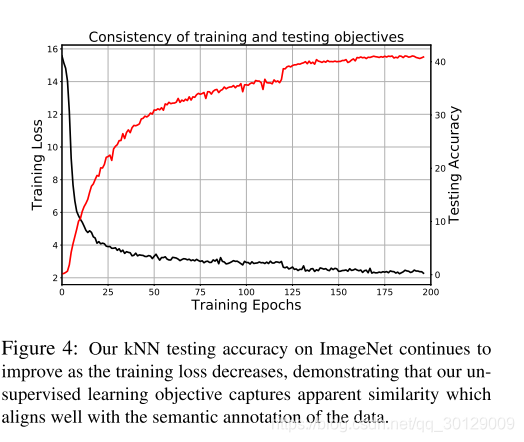

The embedding feature size.
我们研究当我们改变嵌入尺寸从32到256时，性能是如何变化的。表4显示，性能从32增加到128，趋于饱和，接近256。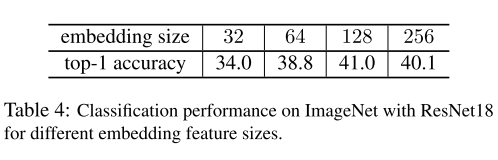

Training set size
为了研究我们的方法如何扩展数据大小，我们用不同大小的ImageNet数据训练不同的表示法，并使用最近邻来评估完全标记集的分类性能。表5显示，我们的特征学习方法受益于更大的训练集，并且随着训练集的增长，测试的准确性也会提高。这个特性对于成功的无监督学习是至关重要的.
Qualitative case study
为了说明所学习的特征，图5显示了使用所学习的特征进行图像检索的结果。前四行显示了最好的情况.所有前10个结果都与查询属于相同的类别。下面四行显示的是最糟糕的情况，前10名都不在同一类别中。然而，即使在失败的情况下，检索到的图像仍然与查询非常相似，这证明了我们的非监督学习目标的有效性.

5. Summary

我们提出了一种无监督的特征学习方法，通过一种新的非参数softmax公式,来最大限度地区分实例。监督学习产生了明显的图像相似性，这是由监督学习的思想所驱动的。我们的实验结果表明，我们的方法在ImageNet和Places上的图像分类性能优于最先进的方法.具有紧凑的128维的代表性，可以很好地处理更多的数据和更深入的网络工作。它还提供了半监督学习和目标检测任务的竞争性泛化结果.

来源：CSDN

作者：ML_NI_CSU

链接：https://blog.csdn.net/lj695242104/article/details/103533705