目录:
- 《剑指offer》面试题-topk算法
- 搜索热词关联算法
- 代码实现以及java学习
写在前面
每次写博客都爱先扯点乱七八糟的东西,这是工作准备写的第2篇博客,之前写过一篇hadoop入门,那里还留下了一个搜索引擎的demo没有去完成,这次学习热词关联刚好也是和搜索引擎相关,所以借此机会把这篇记录下来,一方面花了3天来学习了这个内容,确实学到了不少东西,二来下次写搜索引擎的hadoop的demo时候可以把这个整合到一起,如果有空把关于搜索的东西整合到一起,添加一些爬虫相关的只是内容,就可以简单的搭建一个搜索引擎了,想想还是挺不错的。好啦,我们来开始学习吧!
topK算法
这个题目实现不难,在没有什么限制的情况下我们很快能得到答案。
解法1 排序
对数组排序,然后找到最小的k个数字,这个思路和粗暴,实际上我们把问题转化成了排序算法,那么合理的想法就是去找排序中时间复杂度最小的快排(O(nlgn)),这里对于此方法有一个问题就是在于需要改变原数组,如果题目中存在此种限制,自然是需要考虑其他算法。
解法2 partition算法
parition算法,说起这个算法可能对于算法不太熟悉的同学真没什么印象,但是如果说快排大家肯定都知道了。我先贴一段java实现的代码给大家看一看。
//快速排序 虽然快排思想比较简单,但是有些=还是需要注意一下勒,网上不少博客的代码都有点小问题,所以自己写了跑了下才贴出来。
public static void qsort(int[] arr,int begin,int end) {
int index = partition(arr, begin,end);
if(begin >= end -1) {
return;
}
qsort(arr,begin,index-1);
qsort(arr,index+1,end);
}
//用一个哨兵来分割大于小于的两部分
private static int partition(int[] arr,int begin,int end) {
if(begin >= end) {
return -1;
}
int pos = arr[begin];
while(begin < end) {
while(arr[end] >= pos && begin < end) {
end --;
}
if(begin < end) {
arr[begin] = arr[end];
}
while(arr[begin] <= pos && begin < end) {
begin ++;
}
if(begin < end) {
arr[end] = arr[begin];
}
}
arr[begin] = pos;
return begin;
}以上代码中有很重要的一块就是partition,很多快排的写法里面没有将其作为单独的一个函数,他的思想就是取出一个哨兵,然后把大于他的放到一边,小于他的放到另一边。这样如果我们按着这个思路,先找到一个数partition一次,判断这个树的最终位置是不是在k处,如果大于则找前面的部分(假设左小右大),如此直到我们找到第k个值的位置,此时k之前的都比k小,就得到了题解。下面我大概举个例子,给大家一个形象的表示。
arr = 4,3,5,9,2,4,6 找到最小的3个值
partition1 2 3 4 9 5 4 6 index = 3 分了一次刚好index返回3,所以最小的是2 3 4,对没毛病!
那我们现在来看一看这个算法的时间复杂度,逆序的时候复杂度最高为O(n^2),如果是随机的话,T(N) = T(T/2) + N,时间复杂度为O(N)。那么我们可以在O(N)的时间复杂度把这个问题给解决了。这比上述排序好多了,因为针对上述排序中,我们每次都要把序列找到一个哨兵然后左右都要去排序,这个时候,我们只处理我们需要处理的部分,时间复杂度就降低了下来。虽然简单,还是画个图表示一下下。如下图,如果我们想要去找前3小的数字时,如果哨兵是5,那么我们就可以不用管后面部分,只需要考虑前面绿色填充的数字,这样节约了很多时间。
但是这个算法仍然有点问题,同解法1,这个算法会调整数据,当数据量不断增加时,我们有时候希望能增量式的去处理,而不是每次有数据进来都乾坤大挪移,那么我们需要考虑外部存储来辅助这个算法保证这个原数组不会改变。
解法3 外部存储-小(大)根堆
我们日常也会遇到这样的算法例子,偶尔我们会用一个外部数组来存储,每次进来一个数字就判断。比如我们想找一个数组里面最大的3个数字,我开一个3空间的数组,那么我们遍历一次原数组,找到最大的3个依次放入,每次放入时和外部数组比较一下,这样也可以在O(N)时间内完成,且不改变原数组,好啦。貌似我们对这个算法已经了解的很深入了。
且慢,各位看客想一想,如果这个N非常非常大时候,如果我们要在几百万的数据中找前10,那会有什么不同么。对于算法复杂度来说,O(N)应该是不可避免了,至少每个数字都要遍历到,但是对于大数据处理来说,复杂度中隐藏的时间常熟因子也是十分关键的。我们现在来分析一波,对于外部数组,如果我们是找最大的K个数,那么我们每次需要找到数组中最小的,如果最小我们就要替换,所以会有替换操作。那么对于一个无顺序数组的话,大概O(K)可以完成,然后我们算法整体就是O(K*N),如果我们来维护一个有序数组的话,开销没什么区别。如果熟悉数据结构的同学,现在一定看出问题了,我们需要用堆来完成这些操作,取最小堆可以O(1),来完成,而插入堆也可以在O(lgN)完成(平均),OK,数据量一大时候,这个差异是非常大的,先给大家看一个感性的认识,我没有具体去算时间,只是进行了一下对比,heap为我自己实现的小根堆,orderarr是网上借鉴的别人实现的有序数组。下面应该十分明显了,k小时没有啥区别,k的变大,这个差距会越来越大。
int n = 3000000;
int k = 100;
orderarr程序运行时间: 16ms
heap程序运行时间: 13ms
int n = 3000000;
int k = 100000;
orderarr程序运行时间: 5137ms
heap程序运行时间: 59ms
算法不难,此处介绍一下思路即可,晚上有很多介绍堆思路的,算法导论中有heapify来维护堆的,java中的优先队列好像是用shiftup,shitfdown来维护insert操作,个人觉得都可以,思想都是一致的。大家有兴趣可以翻翻我的github,文末给出,我把这些代码都放在里面,有不对之处大家也可以指教。
public static void testHeap(int n,int k) {
int[] arr = new int[n];
Random random = new Random();
for(int i=0;i<arr.length;i++) {
arr[i] = random.nextInt();
}
int length = arr.length;
MinHeap mHeap = new MinHeap();
long startTime=System.currentTimeMillis(); //获取开始时间
for(int i=0;i<length;i++) {
if(i<=k-1) {
mHeap.insert(arr[i]);
}else {
if(arr[i] > mHeap.getTop()) {
mHeap.removeTop();
mHeap.insert(arr[i]);
}
}
}
// mHeap.show();
long endTime=System.currentTimeMillis(); //获取结束时间
System.out.println("heap程序运行时间: "+(endTime-startTime)+"ms");
}热词搜索提示
现在终于到正题了,之前半天都是在介绍算法,现在也讲讲该算法的应用,现在xx搜索引擎公司需要根据用户的输入来给其他用户做输入提示,那么我们有很多输入词条,现在需要提示热度最高的。这实际就是一个topK问题,额外之处一个是操作对象不在是一个整数,而是一个键值对,另外一个问题是我们需要构建一颗trie树来帮助我们找到需要排序的词语。当然对于日志信息来说,数据是一条一条的,我们还需要用到hash表来帮我们进行统计。
第一步 hashMap统计
对于hash表来说,没有特别要多说的,统计一个大数据量,如果内存够的话,一张hash表无疑是很好的选择,O(n)的时间就可以搞定,当然这个大数据也是有一个限制的,如果上T或者更大,那可能就需要想其他的办法了。G级别的这个还是没问题的。此处我们使用java中的hashMap来完成。
第二步 构建trie树
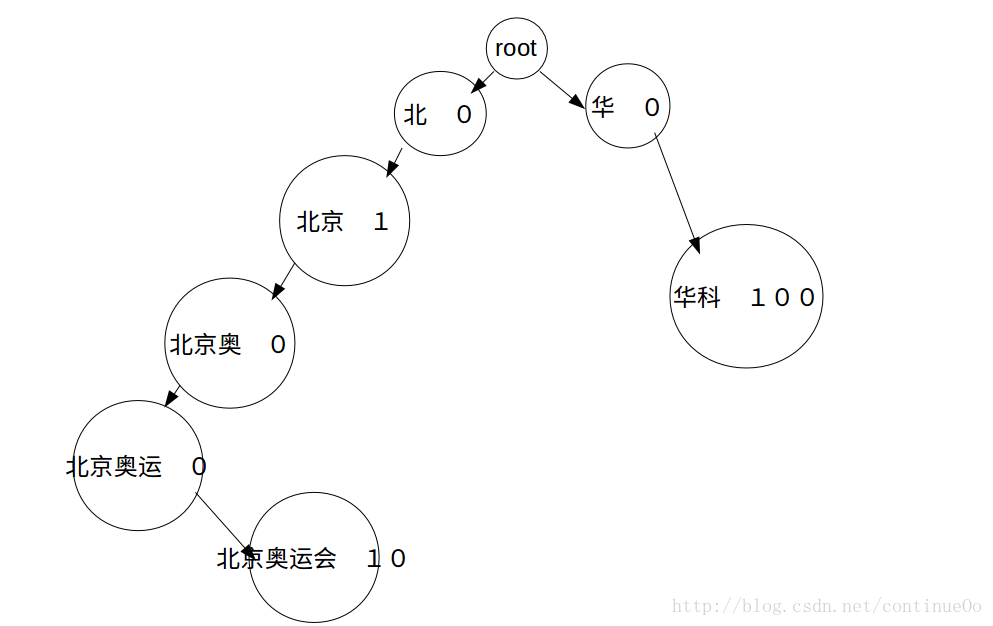
因为涉及到应用,当输入“北”的时候,希望能提示“北京”,或者“北海”,不能提示“南京”吧,那么我们需要有一颗前缀树来实现,每次找到输入的节点的子树,对子树中的节点遍历,取得最大的K个,为了方便,前缀树结构如下,每个节点放置到当前节点位置的所有字符,并且添加对应频次,路过的词语频次为0,结构图大致如下。
第三部 topK算法
topK说的很多了,我们需要改成能针对键值对的就OK啦! ~^_^~
代码实现以及java学习
决策树部分
下面是决策树的实现,决策树中学习到的一个比较重要的点就是需要自己实现一个迭代器,之前的数组可以直接遍历,for循环就可以了,但是树没有这么简单,便需要实现一个iterator来帮助完成遍历。
首先class需要实现Iterable接口,调用x.iterator()返回一个Iterator类,这个类通常含有2个方法,hasnext(),next()。结构如下,具体请查看其他介绍,此处不赘述。
public class MyIteratorClass implements Iterable{
@Override
public Iterator iterator() {
// TODO Auto-generated method stub
return new MyIterator;
}
private class MyIterator implements Iterator<TrieNode>{
@Override
//返回是否还有下一个值
public boolean hasNext() {
return null;
}
@Override
//返回下一个迭代的值
public TrieNode next() {
return null;
}import java.util.ArrayList;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import datastructure.TrieTree.TrieNode;
public class TrieTree implements Iterable{
private TrieNode root;
public static void main(String[] args) {
TrieTree trieTree = new TrieTree();
trieTree.insert("北京动物园", 2);
trieTree.insert("北京天安门", 3);
trieTree.insert("北京", 1);
String word = "北京";
TrieNode subTree = trieTree.getSubTreeByWord(word);
Iterator<TrieNode> iterator = trieTree.iterator(subTree);
while(iterator.hasNext()) {
TrieNode node = iterator.next();
System.out.println(node.value + " " + node.count);
}
//trieTree.showTrieTree();
}
public TrieNode getRoot() {
return root;
}
public TrieTree() {
root = new TrieNode("root",0);
}
public class TrieNode{
private String value;
private ArrayList<TrieNode> son;
private int count; //当前路径上统计数
public TrieNode() {
// TODO Auto-generated constructor stub
this.value = "null";
this.count = 0;
this.son = new ArrayList<TrieNode>();
}
public TrieNode(String value,int count) {
// TODO Auto-generated constructor stub
this.value = value;
this.count = count;
this.son = new ArrayList<TrieNode>();
}
public String getValue() {
return value;
}
public int getCount() {
return count;
}
}
//根据输入获取子树
public TrieNode getSubTreeByWord(String str) {
return _getSubTreeByWord(root,str);
}
private TrieNode _getSubTreeByWord(TrieNode root,String str) {
int sonNum = root.son == null? 0 :root.son.size();
if(root.value.equals(str)) {
return root;
}
for(int i=0;i<sonNum;i++) {
TrieNode node = _getSubTreeByWord(root.son.get(i),str);
if(node != null) {
return node;
}
}
return null;
}
//插入时,把count放在最后一个节点上
public void insert(String str,int count) {
_insertNode(root, str, count ,1);
}
private void _insertNode(TrieNode root,String str,int count ,int index) {
int sonNum = root.son.size();
int findFlag = 0;
for(int i=0;i<sonNum;i++) {
if(root.son.get(i).value.equals(str.substring(0, index))) {
findFlag = 1;
if(str.length() == index) {
root.son.get(i).count = count;
return;
}else {
_insertNode(root.son.get(i), str, count ,index+1);
}
break;
}
}
//遍历之后没有找到就创建一个
if(findFlag == 0) {
// System.out.println(str.substring(0, index));
String newValue = str.substring(0, index);
int newCount = index != str.length() ? 0 : count;
TrieNode sonNode = new TrieNode(newValue,newCount);
root.son.add(sonNode);
if(str.length() != index) {
_insertNode(sonNode, str, count ,index+1);
}
}
}
//循环遍历输出字典树内容
public void showTrieTree() {
_showTrieTree(root);
}
private void _showTrieTree(TrieNode root) {
System.out.println(root.value + root.count);
int sonNum = root.son.size();
for(int i=0;i<sonNum;i++) {
_showTrieTree(root.son.get(i));
}
}
@Override
public Iterator<TrieNode> iterator() {
// TODO Auto-generated method stub
return new TrieTreeIterator();
}
public Iterator<TrieNode> iterator(TrieNode itrRoot) {
// TODO Auto-generated method stub
return new TrieTreeIterator(itrRoot);
}
private class TrieTreeIterator implements Iterator<TrieNode>{
private TrieNode next;
private Queue<TrieNode> queue;
public TrieTreeIterator() {
// TODO Auto-generated constructor stub
next = root;
queue = new LinkedList<TrieNode>();
if(next == null) {
return;
}
}
public TrieTreeIterator(TrieNode itrRoot) {
// TODO Auto-generated constructor stub
next = itrRoot;
queue = new LinkedList<TrieNode>();
if(next == null) {
return;
}
}
@Override
public boolean hasNext() {
// TODO Auto-generated method stub
int sonNum = next.son.size();
for(int i=0;i<sonNum;i++) {
queue.add(next.son.get(i));
}
if(queue.isEmpty()) {
return false;
}else {
return true;
}
}
@Override
public TrieNode next() {
// TODO Auto-generated method stub
next = queue.remove();
return next;
}
}
} Heap部分
此处借鉴了网友的代码,但是不记得哪里抄来的了,抱歉。
这里学到的比较重要的东西就是泛型的使用,对于这份代码来说,是适用与int的,但是我想拿这份代码来做键值对的处理,利用泛型和提供的Comparator就可以很方便的实现代码的复用。此处我定义了键值对的类型,提供了一些基础方法。然后出现了另外一个重要的问题,那就是关于对象复制的问题,这里学习了深克隆的方式,如果setRoot方法不传入clone(),则只是传入了索引,而不是对堆内进行赋值,这样逻辑上有误。所以这里传入一定是clone的内容。关于clone有深浅之分,这里我使用了序列化的方式,下面这博客写的不错,推一推。
克隆学习:https://www.cnblogs.com/Qian123/p/5710533.html
//代码复用可以学习的地方
//这是之前的代码
int[] arr = new int[n]
//此处省略,很多,这里重点在于描述差异之处
mHeap.setRoot(arr[i]);
//这是修改后的代码
KeyPair<String, Integer> tempKeyPair = new KeyPair<String, Integer>("", 0);
mHeap.setRoot(tempKeyPair.clone());
//建立heap来做键值对比较
Comparator<KeyPair<String, Integer>> comp = new Comparator<KeyPair<String, Integer>>() {
@Override
public int compare(KeyPair<String, Integer> o1, KeyPair<String, Integer> o2) {
// TODO Auto-generated method stub
return o2.getValue() - o1.getValue();
}
}; //克隆可以学习的部分,序列化方式克隆。
public class KeyPair<K, V> implements Serializable {
private K key;
private V value;
public KeyPair clone() {
KeyPair outer = null;
try { // 将该对象序列化成流,因为写在流里的是对象的一个拷贝,而原对象仍然存在于JVM里面。所以利用这个特性可以实现对象的深拷贝
ByteArrayOutputStream baos = new ByteArrayOutputStream();
ObjectOutputStream oos = new ObjectOutputStream(baos);
oos.writeObject(this);
// 将流序列化成对象
ByteArrayInputStream bais = new ByteArrayInputStream(baos.toByteArray());
ObjectInputStream ois = new ObjectInputStream(bais);
outer = (KeyPair) ois.readObject();
} catch (IOException e) {
e.printStackTrace();
} catch (ClassNotFoundException e) {
e.printStackTrace();
}
return outer;
}
}
public class Heap<T> {
/**
* 以数组形式存储堆元素
*/
private T[] heap;
/**
* 用于比较堆中的元素。c.compare(根,叶子) > 0。
* 使用相反的Comparator可以创建最大堆、最小堆。
*/
private Comparator<T> c;
public Heap(T[] a, Comparator<T> c) {
this.heap = a.clone();
this.c = c;
buildHeap();
}
/**
* 返回值为i/2
*
* @param i
* @return
*/
private int parent(int i) {
return (i - 1) >> 1;
}
/**
*
* 返回指定节点的left子节点数组索引。相当于2*(i+1)-1
*
*
* @param i
* @return
*/
private int left(int i) {
return ((i + 1) << 1) - 1;
}
/**
* 返回指定节点的right子节点数组索引。相当于2*(i+1)
*
* @param i
* @return
*/
private int right(int i) {
return (i + 1) << 1;
}
/**
* 堆化
*
* @param i
* 堆化的起始节点
*/
private void heapify(int i) {
heapify(i, heap.length);
}
/**
* 堆化,
*
* @param i
* @param size 堆化的范围
*/
private void heapify(int i, int size) {
int l = left(i);
int r = right(i);
int next = i;
if (l < size && c.compare(heap[l], heap[i]) > 0)
next = l;
if (r < size && c.compare(heap[r], heap[next]) > 0)
next = r;
if (i == next)
return;
swap(i, next);
heapify(next, size);
}
/**
* 对堆进行排序
*/
public void sort() {
// buildHeap();
for (int i = heap.length - 1; i > 0; i--) {
swap(0, i);
heapify(0, i);
}
}
/**
* 交换数组值
*
* @param arr
* @param i
* @param j
*/
private void swap(int i, int j) {
T tmp = heap[i];
heap[i] = heap[j];
heap[j] = tmp;
}
/**
* 创建堆
*/
private void buildHeap() {
for (int i = (heap.length) / 2 - 1; i >= 0; i--) {
heapify(i);
}
}
public void setRoot(T root) {
heap[0] = root;
heapify(0);
}
public T root() {
return heap[0];
}
public T getByIndex(int i) {
if(i<heap.length) {
return heap[i];
}
return null;
}
}总结
上面贴出了测试数据和最终结果,以上代码估计跑不通,贴出来是为了突出重点,如果想看跑,可以follow我的github,上面有完整实例,另外还有一些问题没有解决完全,一个是大数据下的测试,另外有一个就是交互问题,因为考虑到后面还会写相关搜索引擎的板块,所以这里先不急着完善,以后有机会再做交互和完整测试。
哈,写了3个多小时,终于总结完了~,看完有收货的小伙伴,记得赞一个噢~。我们一起天天学算法~
来源:CSDN
作者:continueOo
链接:https://blog.csdn.net/continueOo/article/details/77428696