一、简介
在GBDT的迭代中,假设我们前一轮迭代得到的强学习器是ft-1(x)损失函数是L(y,ft-1(x)) 我们本轮迭代的目标是学习到弱学习器ht(x),让本轮的损失L(t,ft-1(x)+ht(x))最小。
假如有个人30岁,我们首先用20岁去拟合,发现损失有10岁,这时我们用6岁去拟合剩下的损失,发现差距还有4岁,第三轮我们用3岁拟合剩下的差距,差距就只有一岁了。如果我们的迭代轮数还没有完,可以继续迭代下面,每一轮迭代,拟合的岁数误差都会减小。
也就是说我们要求的是高偏差,然后一步一步慢慢缩小这个偏差。
二、负梯度拟合
初始化若学习分类器是:
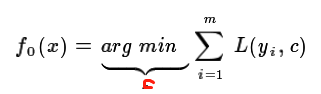
每一轮都有一个损失函数要去拟合,因为是偏差,所以找不到一个真实值来去拟合。因此提出了一种方法:用损失函数的负梯度来拟合本轮损失的近似值,进而拟合一个cart回归树。
第t轮的第i个样本的损失函数的负梯度表示为:

利用(xi,rti)(i=1,2,...m),我们可以拟合一颗CART回归树,得到了第t颗回归树,其对应的叶节点区域Rtj,j=1,2,...,J。其中J为叶子节点的个数。
每个叶子节点里有多个样本,然后求出使损失函数最小时的输出值ctj(类似于标签):
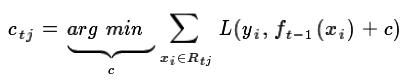
这样我们就得到了本轮的决策树拟合函数如下:
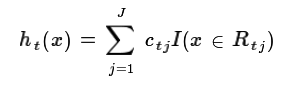
本轮最终得到的强学习器的表达式如下:
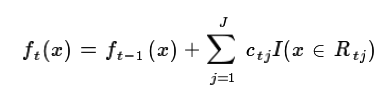
三、GBDT常用损失函数
分类
指数损失函数:![]()
对数损失函数:
回归
均方差;
绝对损失
四、GBDT的正则化
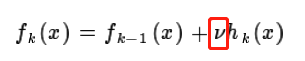
五、优缺点
GBDT主要的优点有:
1) 可以灵活处理各种类型的数据,包括连续值和离散值。
2) 在相对少的调参时间情况下,预测的准确率也可以比较高。这个是相对SVM来说的。
3)使用一些健壮的损失函数,对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。
GBDT的主要缺点有:
1)由于弱学习器之间存在依赖关系,难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。