字符串匹配有KMP,BM,SUNDAY算法。
https://www.cnblogs.com/ZuoAndFutureGirl/p/9028287.html
KMP核心就是next数组(pattern接下来向后移动的位数) (text 当前匹配到的index不变)
模式串向右移动的位数为:失配字符所在位置 - 失配字符对应的next 值
即移动的实际位数为:j - next[j],且此值大于等于1。
操作为
if(text[i]!=p[j])
j=next[j]; // next[j] 即为p[0,j-1]串中最长前后缀长度. p[j]与text[i]失配,但text[X,i-1]与p[0,j-1]匹配,其中最长前后缀也匹配,直接移动pattern,前缀覆盖后缀,比较下一位p[k]与text[i]是否匹配
//p[next[j]] 即为最长前后缀后面一位p[k]
//k为 next[j]. 即p[0,j-1]串最长前后缀的长度
next求法:
next[0]=-1 //若text[i]与pattern第一个字符失配,直接向后移动pattern一位
k =next [j] // j-1串中,最长的前后缀长度为k
if p[j]==p[k] //j串中最长前后缀长度为k+1
next[j + 1] = next[j] + 1
else
k=next[k] //画个图就很好想.
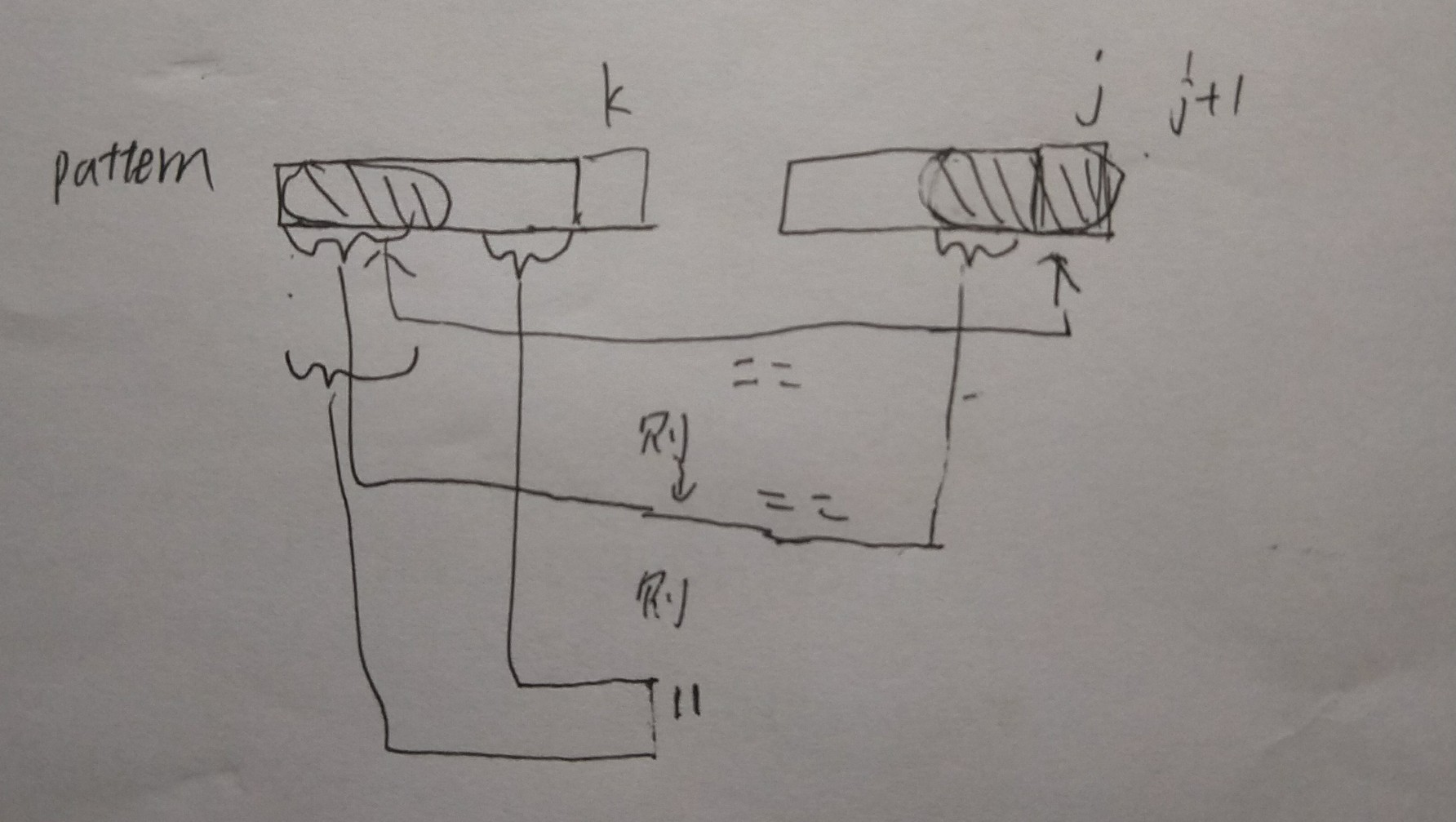
void GetNext(char* p,int next[])
{
int pLen = strlen(p);
next[0] = -1;
int k = -1;
int j = 0;
while (j < pLen - 1)
{
//p[k]表示前缀,p[j]表示后缀
if (k == -1 || p[j] == p[k])
{
++k;
++j;
next[j] = k;
}
else
{
k = next[k];
}
}
}
next优化:
问题出在不该出现p[j] = p[ next[j] ]。
理由是:当p[j] != text[i] 时,下次匹配必然是p[ next [j]] 跟text[i]匹配,如果p[j] = p[ next[j] ],必然导致后一步匹配失败
(因为p[j]已经跟s[i]失配,然后你还用跟p[j]等同的值p[next[j]]去跟s[i]匹配,很显然,必然失配),
所以不能允许p[j] = p[ next[j ]]。如果出现了p[j] = p[ next[j] ],则需要再次递归,即令next[j] = next[ next[j] ]。
所以,咱们得修改下求next 数组的代码。
//优化过后的next 数组求法
void GetNextval(char* p, int next[])
{
int pLen = strlen(p);
next[0] = -1;
int k = -1;
int j = 0;
while (j < pLen - 1)
{
//p[k]表示前缀,p[j]表示后缀
if (k == -1 || p[j] == p[k])
{
++j;
++k;
//较之前next数组求法,改动在下面4行
if (p[j] != p[k])
next[j] = k; //之前只有这一行
else
//因为不能出现p[j] = p[ next[j ]],所以当出现时需要继续递归,k = next[k] = next[next[k]]
next[j] = next[k];
}
else
{
k = next[k];
}
}
}
因为比较熟悉KMP,就用KMP了
class Solution {
public:
vector<int> getnext(string str)
{
int len=str.size();
vector<int> next;
next.push_back(-1);//next数组初值为-1
int j=0,k=-1;
while(j<len-1)
{
if(k==-1||str[j]==str[k])//str[j]后缀 str[k]前缀
{
j++;
k++;
if(str[j]!=str[k])
next.push_back(k);
else
next.push_back(next[k]);
}
else
{
k=next[k];
}
}
return next;
}
int strStr(string haystack, string needle) {
if(needle.empty())
return 0;
int i=0;
int j=0;
int len1=haystack.size();
int len2=needle.size();
vector<int> next;
next=getnext(needle);
while((i<len1)&&(j<len2))
{
if((j==-1)||(haystack[i]==needle[j]))
{
i++;
j++;
}
else
{
j=next[j];//获取下一次匹配的位置
}
}
if(j==len2)
return i-j;
return -1;
}
};
然后看题解,有SunDay算法,更好理解(https://leetcode-cn.com/problems/implement-strstr/solution/python3-sundayjie-fa-9996-by-tes/)
偏移表告诉我们下一步可能匹配需要移动的最小步数
设text,patternlen=len
核心思想就是当前匹配若失败,那么当前text中开始匹配的位置i+len-1必不可能匹配上。此时检查i+len处的字符,当其等于pattern中的某个字符(从右向左找),则将pattern移动使text[i+len]与pattern中相应字符对应。
然后重复。
若没有匹配上,那么直接移动len+1
最坏情况:O(nm)
平均情况:O(n)
(实际提交的 时候,确实sunday比kmp快一点。可能是测试用例的关系)
class Solution {
public:
int strStr(string haystack, string needle) {
if(needle.empty())
return 0;
int slen=haystack.size();
int tlen=needle.size();
if(slen<tlen)
return -1;
int i=0,j=0;//i指向源串首位 j指向子串首位
int k;
int m=tlen;//第一次匹配时 源串中参与匹配的元素的下一位
while(i<slen)
{
if(haystack[i]!=needle[j])
{
for(k=tlen-1;k>=0;k--)//遍历查找此时pattern与源串[i+tlen+1]相等的最右位置
{
if(needle[k]==haystack[m])
break;
}
i=m-k;//i为下一次匹配源串开始首位 Sunday算法核心:最大限度跳过相同元素
j=0;//j依然为子串首位
m=i+tlen;//m为下一次参与匹配的源串最后一位元素的下一位
if(m>slen)
return -1;
}
else
{
if(j==tlen-1)//若j为子串末位 匹配成功 返回源串此时匹配首位
return i-j;
i++;
j++;
}
}
return -1;//当超过源串长度时
}
};
还有bm算法 O(N) - O(M+N)
class Solution {
public:
void get_bmB(string& T,vector<int>& bmB)//坏字符
{
int tlen=T.size();
for(int i=0;i<256;i++)//不匹配直接移动子串
{
bmB.push_back(tlen);
}
for(int i=0;i<tlen-1;i++)//靠右原则
{
bmB[T[i]]=tlen-i-1;
}
}
void get_suff(string& T,vector<int>& suff)
{
int tlen=T.size();
int k;
for(int i=tlen-2;i>=0;i--)
{
k=i;
while(k>=0&&T[k]==T[tlen-1-i+k])
k--;
suff[i]=i-k;
}
}
void get_bmG(string& T,vector<int>& bmG)//好后缀
{
int i,j;
int tlen=T.size();
vector<int> suff(tlen+1,0);
get_suff(T,suff);//suff存储子串的最长匹配长度
//初始化 当没有好后缀也没有公共前缀时
for(i=0;i<tlen;i++)
bmG[i]=tlen;
//没有好后缀 有公共前缀 调用suff 但是要右移一位 类似KMP里的next数组
for(i=tlen-1;i>=0;i--)
if(suff[i]==i+1)
for(j=0;j<tlen-1;j++)
if(bmG[j]==tlen)//保证每个位置不会重复修改
bmG[j]=tlen-1-i;
//有好后缀 有公共前缀
for(i=0;i<tlen-1;i++)
bmG[tlen-1-suff[i]]=tlen-1-i;//移动距离
}
int strStr(string haystack, string needle) {
int i=0;
int j=0;
int tlen=needle.size();
int slen=haystack.size();
vector<int> bmG(tlen,0);
vector<int> bmB;
get_bmB(needle,bmB);
get_bmG(needle,bmG);
while(i<=slen-tlen)
{
for(j=tlen-1;j>-1&&haystack[i+j]==needle[j];j--);
if(j==(-1))
return i;
i+=max(bmG[j],bmB[haystack[i+j]]-(tlen-1-j));
}
return -1;
}
};
作者:2227
链接:https://leetcode-cn.com/problems/implement-strstr/solution/c5chong-jie-fa-ku-han-shu-bfkmpbmsunday-by-2227/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。