一直有听说拓扑排序这个很神奇的算法,一开始总觉得它是类似快排一样的排序算法,今天看了一下,发现并不是这样的。
理解
拓扑排序还是图论中的知识,它是图论中有向图的一种应用,因为有向图中两个节点之间的连接是有头和尾的,不像无向图。所以,我们规定,1:遍历网时,我们顺着一条边往下走的时候,一定是只能从尾走向头,并且只有以某节点为头的所有尾节点都走完的时候,才能继续顺着往下走。2:图中的节点不能成环,也就是说最后输出的顶点数一定要等于总的节点数,少了一个就说明这个网存在环。(其实可以这样子理解,当某节点(活动)的所有先决条件(节点或者叫活动)完成的时候,该节点才能顺利往下走,当网中存在环的时候,可以理解为某个活动完成的以自己完成的为前提的,这就不符合逻辑了)。
拓扑排序算法
所谓的拓扑排序。就是对一张有向图构造拓扑序列的过程,构造时会有“两种”结果,当网点的所有节点都被输出的时候,说明这个图(网)是不存在环的,当输出的节点小于总节点数时,说明这个图(网)是存在的环的。
假定给了一张这样的图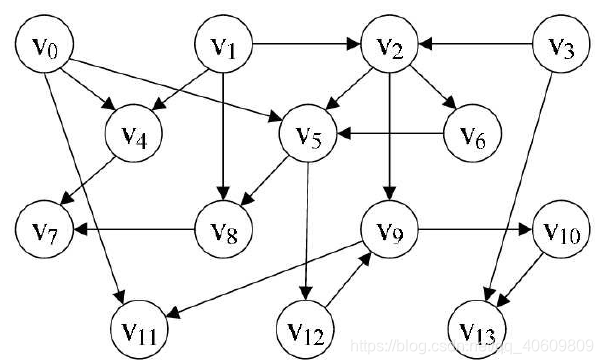
从前面的知识可以知道,对于有向图我们是倾向于用链接链表这样的数据结构的,但是此时我们要在连接链表的基础上增加一个数据位(indata),表示为每个节点的入度。
基本思路:我们从图(网)中选择一个入度为0的顶点输出,并且将该顶点删除,在删除该顶点的时候,需要把以该节点为尾的顶点的入度减一 然后继续选择一个入度为0的顶点重读此步骤,直到最后图(网)中没有了入度为0的节点。
应该把数据存放成这种结构中去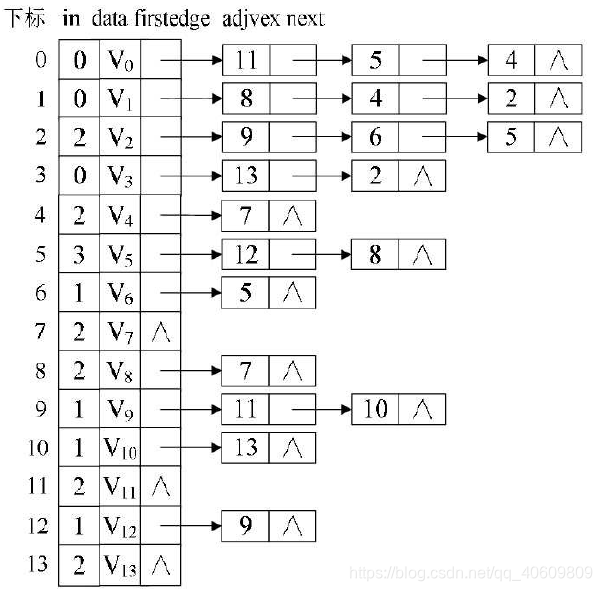
基础数据结构
//图的邻接链表存储结构
//边表节点结构,一个adjvex用来存储邻接点的位置,一个next指针用来指向下一个节点
typedef struct EdgeNode
{
int adjvex; //存储顶点下标信息
struct EdgeNode *next;
} EdgeNode;
//顶点表节点结构
typedef struct
{
int indata; //!!!相比于普通的数据结构,新增了一个这个辅助数据位!!!
string Vexs; //用来存储顶点信息
EdgeNode *firstedge; //用来存储当前顶点的下一个顶点
} VexList;
//这里用动态数组存储顶点表,然后numVertex,numEdge是一个图的顶点数和边数
typedef struct
{
vector<VexList> VexList;
int Vertexs, Edges;
} GraphList;
核心算法,此处需要用到一个辅助数据结构(栈),用来存储入度为0的顶点,目的是为了每次查找顶点表中有哪些是入度为0的顶点不用去遍历整个顶点表。当然用队列也是可以的,等会可以再发散想下
核心代码
bool ToplogicalSort(GraphList *GL)
{
EdgeNode *e;//用来存储入度为0的节点
int cnt;//用来统计输出节点的个数
stack<int > Rd_zero;
for(int i=0;i<GL->Vertexs;++i){
if(GL->VexList[i].indata==0){ //入度为0的节点
Rd_zero.push(i);
}
}
while(!Rd_zero.empty()){
int outtop = Rd_zero.top();
Rd_zero.pop();
cout<<outtop<<",";
cnt++;
for(e=VexList[outtop].firstedge;e!=NULL;e=e->next){
int k = e->adjvex;
if((--VexList[k].indata)==0){//如果这个顶点的入度现在为0了,再次入栈
Rd_zero.push(k);
}
}
}
if(cnt==GL->Vertexs)
return true;
else//存在环
return false;
}
拓扑序列的输出结果很多,这里就不写出来了。个人觉得这个函数可以将输出改为输出到一个结果组数或者是一个结果队列中,然后根据函数返回值的类型,决定要不要这个输出的结果。
还有一个就是,因为入度为0的辅助数据结构是栈,其实还可以是队列,这样子的话,就增加了输出结果的多样性。但是结果不能违背上面的两个原则。。。整个算法的时间负复杂度为O(n+e)。
来源:https://blog.csdn.net/qq_40609809/article/details/102776295