Problem with Precision floating point operation in C

Question

For one of my course project I started implementing \"Naive Bayesian classifier\" in C. My project is to implement a document classifier application (especially Spam) using huge

Answer 1

Your problem is caused because you are collecting too many terms without regard for their size. One solution is to take logarithms. Another is to sort your individual terms. First, let's rewrite the equation as 1/p = 1 + ∏((1-p_i)/p_i). Now your problem is that some of the terms are small, while others are big. If you have too many small terms in a row, you'll underflow, and with too many big terms you'll overflow the intermediate result.

So, don't put too many of the same order in a row. Sort the terms (1-p_i)/p_i. As a result, the first will be the smallest term, the last the biggest. Now, if you'd multiply them straight away you would still have an underflow. But the order of calculation doesn't matter. Use two iterators into your temporary collection. One starts at the beginning (i.e. (1-p_0)/p_0), the other at the end (i.e (1-p_n)/p_n), and your intermediate result starts at 1.0. Now, when your intermediate result is >=1.0, you take a term from the front, and when your intemediate result is < 1.0 you take a result from the back.

The result is that as you take terms, the intermediate result will oscillate around 1.0. It will only go up or down as you run out of small or big terms. But that's OK. At that point, you've consumed the extremes on both ends, so it the intermediate result will slowly approach the final result.

There's of course a real possibility of overflow. If the input is completely unlikely to be spam (p=1E-1000) then 1/p will overflow, because ∏((1-p_i)/p_i) overflows. But since the terms are sorted, we know that the intermediate result will overflow only if ∏((1-p_i)/p_i) overflows. So, if the intermediate result overflows, there's no subsequent loss of precision.

Answer 2

Try computing the inverse 1/p. That gives you an equation of the form 1 + 1/(1-p1)*(1-p2)...

If you then count the occurrence of each probability--it looks like you have a small number of values that recur--you can use the pow() function--pow(1-p, occurences_of_p)*pow(1-q, occurrences_of_q)--and avoid individual roundoff with each multiplication.

Answer 3

Here's a trick:

for the sake of readability, let S := p_1 * ... * p_n and H := (1-p_1) * ... * (1-p_n), 
then we have:

  p = S / (S + H)
  p = 1 / ((S + H) / S)
  p = 1 / (1 + H / S)

let`s expand again:

  p = 1 / (1 +  ((1-p_1) * ... * (1-p_n)) / (p_1 * ... * p_n))
  p = 1 / (1 + (1-p_1)/p_1 * ... * (1-p_n)/p_n)

So basically, you will obtain a product of quite large numbers (between 0 and, for p_i = 0.01, 99). The idea is, not to multiply tons of small numbers with one another, to obtain, well, 0, but to make a quotient of two small numbers. For example, if n = 1000000 and p_i = 0.5 for all i, the above method will give you 0/(0+0) which is NaN, whereas the proposed method will give you 1/(1+1*...1), which is 0.5.

You can get even better results, when all p_i are sorted and you pair them up in opposed order (let's assume p_1 < ... < p_n), then the following formula will get even better precision:

  p = 1 / (1 + (1-p_1)/p_n * ... * (1-p_n)/p_1)

that way you devide big numerators (small p_i) with big denominators (big p_(n+1-i)), and small numerators with small denominators.

edit: MSalter proposed a useful further optimization in his answer. Using it, the formula reads as follows:

  p = 1 / (1 + (1-p_1)/p_n * (1-p_2)/p_(n-1) * ... * (1-p_(n-1))/p_2 * (1-p_n)/p_1)

Answer 4

I am not strong in math so I cannot comment on possible simplifications to the formula that might eliminate or reduce your problem. However, I am familiar with the precision limitations of long double types and am aware of several arbitrary and extended precision math libraries for C. Check out:

http://www.nongnu.org/hpalib/ and http://www.tc.umn.edu/~ringx004/mapm-main.html

Answer 5

This happens often in machine learning. AFAIK, there's nothing you can do about the loss in precision. So to bypass this, we use the log function and convert divisions and multiplications to subtractions and additions, resp.

SO I decided to do the math,

The original equation is:

I slightly modify it:

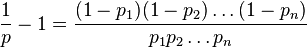
Taking logs on both sides:

Let,

Substituting,

Hence the alternate formula for computing the combined probability:

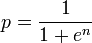
If you need me to expand on this, please leave a comment.

Answer 6

You can use probability in percents or promiles:

doc_spam_prob= (numerator*100/(denom1+denom2));

or

doc_spam_prob= (numerator*1000/(denom1+denom2));

or use some other coefficient