This section of the NLP book is a little confusing I will admit because they don't follow through with the complete calculation of the external measure of cluster entropy, instead they focus on the calculation of an individual cluster entropy calculation. Instead I will try to use a more intuitive set of variables and include the complete method for calculating the external measure of total entropy.
The total entropy of a clustering is:
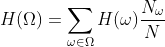
where:
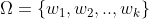is the set of clusters
H(w) is a single clusters entropy
N_w is the number of points in cluster w
N is the total number of points.
Entropy of a cluster w
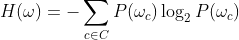
where:
c is a classification in the set C of all classifications
P(w_c) is probability of a data point being classified as c in cluster w.
To make this usable we can substitute the probability with the MLE (maximum likelihood estimate) of this probability to arrive at:
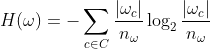
where:
|w_c| is the count of points classified as c in cluster w
n_w is the count of points in cluster w
So in the example given you have 3 clusters (w_1,w_2,w_3), and we will calculate the entropy for each cluster separately, for each of the 3 classifications (x,circle,diamond).
H(w_1) = (5/6)log_2(5/6) + (1/6)log_2(1/6) + (0/6)log_2(0/6) = -.650
H(w_2) = (1/6)log_2(1/6) + (4/6)log_2(4/6) + (1/6)log_2(1/6) = -1.252
H(w_3) = (2/5)log_2(2/5) + (0/5)log_2(0/5) + (3/5)log_2(3/5) = -.971
So then to find the total entropy for a set of clusters, you take the sum of the entropies times the relative weight of each cluster.
H(Omega) = (-.650 * 6/17) + (-1.252 * 6/17) + (-.971 * 5/17)
H(Omega) = -.956
I hope this helps, please feel free to verify and provide feedback.
