In the Fibonacci sequence, is fib(0) 0 or 1 ?
I\'m doing a task in a subject were fib(0) is defined to = 1. But that can\'t be right? fib(0) is 0?
Program with fib(0) = 1; spits out fib(4) = 5
Program w
-
http://en.wikipedia.org/wiki/Fibonacci_number
Fibonacci himself started the sequence with 1 and not 0. It's important to recognize that one's opinion is not unalterable fact, and it may be worthwhile to consider that you don't necessarily know better than the guy who created the sequence. I think it's fine to start the sequence with 0 just as long as you don't act like that is the one and only absolutely correct way of doing things, as the number at "index 0" is fundamentally ambiguous and should always be communicated explicitly.
The question of "index" only applies to us and not Fibonacci. So if we want to go with his starting number and we're using 0-based indexes we'd put his starting number at index 0, or if we're using 1-based indexes we'd put his starting number at index 1.
And since it is indeed possible to continue the sequence to the left, that also makes starting with 0 totally arbitrary. Why not start with -1 and go -1, 1, 0, 1, 1, 2...?
讨论(0) -
The definition with Fib(0) = 1 is known as the combinatorial definition, and Fib(0) = 0 is the classical definition. Both are used in the Fibonacci Quarterly, though authors that use the combinatorial definition need to add a sentence of explanation. Benjamin and Quinn in Proofs that Really Count use f_n for the nth combinatorial Fibonacci number and F_n for the nth classical Fibonacci number. The combinatorial definition is good, not surprisingly for counting questions like "How many ways are there to walk up a flight of n steps, taking either one or two steps at a time?" When n is 0, there's one way to do it, not zero ways.
讨论(0) -
From the Fibonacci number entry on Wikipedia:
In mathematics, the Fibonacci numbers are the following sequence of numbers:

By definition, the first two Fibonacci numbers are 0 and 1, and each remaining number is the sum of the previous two. Some sources omit the initial 0, instead beginning the sequence with two 1s.
In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation
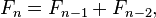
with seed values
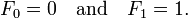 讨论(0)
讨论(0) -
My explanation is for programmers who wants to have simple understanding of this series and about zero term
just start with
first term as f(1) = 1 second term as f(2) = f(1)+nothing Available = f(1)+0 = 1+0 =1 third term as f(3) = f(2)+f(1) = 1+1 = 2it is logical to believe, negative and zero terms are results of the Fibonacci formula using golden ratio
Golden Ratio(GR) value is 1.618034 and formula
f(n) = (GR^n - (1-GR)^n))/sqrt(5)讨论(0)
- 热议问题

 加载中...
加载中...