How to write the Fibonacci Sequence?

Question

I had originally coded the program wrongly. Instead of returning the Fibonacci numbers between a range (ie. startNumber 1, endNumber 20 should = only those numbers between 1

Answer 1

It can be done by the following way.

n = 0

numbers = [0]

for i in range(0,11):
    print n,
    numbers.append(n)
    prev = numbers[-2]
    if n == 0:
        n = 1
    else:
        n = n + prev

Answer 2

Another way of doing it:

a,n=[0,1],10
map(lambda i: reduce(lambda x,y: a.append(x+y),a[-2:]),range(n-2))

Assigning list to 'a', assigning integer to 'n' Map and reduce are 2 of three most powerful functions in python. Here map is used just to iterate 'n-2' times. a[-2:] will get the last two elements of an array. a.append(x+y) will add the last two elements and will append to the array

Answer 3

import time
start_time = time.time()



#recursive solution
def fib(x, y, upperLimit):
    return [x] + fib(y, (x+y), upperLimit) if x < upperLimit else [x]

#To test :

print(fib(0,1,40000000000000))
print("run time: " + str(time.time() - start_time))

Results

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296, 433494437, 701408733, 1134903170, 1836311903, 2971215073, 4807526976, 7778742049, 12586269025, 20365011074, 32951280099, 53316291173, 86267571272, 139583862445, 225851433717, 365435296162, 591286729879, 956722026041, 1548008755920, 2504730781961, 4052739537881, 6557470319842, 10610209857723, 17167680177565, 27777890035288, 44945570212853]

run time: 0.04298138618469238

Answer 4

def fib(x, y, n):
    if n < 1: 
        return x, y, n
    else: 
        return fib(y, x + y, n - 1)

print fib(0, 1, 4)
(3, 5, 0)

#
def fib(x, y, n):
    if n > 1:
        for item in fib(y, x + y, n - 1):
            yield item
    yield x, y, n

f = fib(0, 1, 12)
f.next()
(89, 144, 1)
f.next()[0]
55

Answer 5

A more detailed explanation of how Memoization works for Fibonacci sequence.

# Fibonacci sequence Memoization

fib_cache = {0:0, 1:1}

def fibonacci(n):
    if n < 0:
        return -1
    if fib_cache.has_key(n):
        print "Fibonacci sequence for %d = %d cached" % (n, fib_cache[n])
        return fib_cache[n]
    else:
        fib_cache[n] = fibonacci(n - 1) + fibonacci(n - 2)
    return fib_cache[n]

if __name__ == "__main__":
    print fibonacci(6)
    print fib_cache
    # fibonacci(7) reuses fibonacci(6) and fibonacci(5)
    print fibonacci(7)
    print fib_cache

Answer 6

There is lots of information about the Fibonacci Sequence on wikipedia and on wolfram. A lot more than you may need. Anyway it is a good thing to learn how to use these resources to find (quickly if possible) what you need.

Write Fib sequence formula to infinite

In math, it's given in a recursive form:

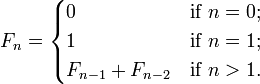
In programming, infinite doesn't exist. You can use a recursive form translating the math form directly in your language, for example in Python it becomes:

def F(n):
    if n == 0: return 0
    elif n == 1: return 1
    else: return F(n-1)+F(n-2)

Try it in your favourite language and see that this form requires a lot of time as n gets bigger. In fact, this is O(2ⁿ) in time.

Go on on the sites I linked to you and will see this (on wolfram):

This one is pretty easy to implement and very, very fast to compute, in Python:

from math import sqrt
def F(n):
    return ((1+sqrt(5))**n-(1-sqrt(5))**n)/(2**n*sqrt(5))

An other way to do it is following the definition (from wikipedia):

The first number of the sequence is 0, the second number is 1, and each subsequent number is equal to the sum of the previous two numbers of the sequence itself, yielding the sequence 0, 1, 1, 2, 3, 5, 8, etc.

If your language supports iterators you may do something like:

def F():
    a,b = 0,1
    while True:
        yield a
        a, b = b, a + b

Display startNumber to endNumber only from Fib sequence.

Once you know how to generate Fibonacci Numbers you just have to cycle trough the numbers and check if they verify the given conditions.

Suppose now you wrote a f(n) that returns the n-th term of the Fibonacci Sequence (like the one with sqrt(5) )

In most languages you can do something like:

def SubFib(startNumber, endNumber):
    n = 0
    cur = f(n)
    while cur <= endNumber:
        if startNumber <= cur:
            print cur
        n += 1
        cur = f(n)

In python I'd use the iterator form and go for:

def SubFib(startNumber, endNumber):
    for cur in F():
        if cur > endNumber: return
        if cur >= startNumber:
            yield cur

for i in SubFib(10, 200):
    print i

My hint is to learn to read what you need. Project Euler (google for it) will train you to do so :P Good luck and have fun!