How can I tell if a point belongs to a certain line?

Question

How can I tell if a point belongs to a certain line?

Examples are appreciated, if possible.

Answer 1

y = m * x + c

This is the equation of a line. x & y are the co-ordinates. Each line is characterized by its slope (m ) and where it intersects the y-axis (c).

So given m & c for a line, you can determine if the point (x1, y1) is on the line by checking if the equation holds for x = x1 and y = y1

Answer 2

A 2D line is generally represented using an equation in two variables x and y here is a well known equation

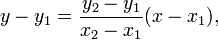
Now imagine your GDI+ line is drawn from (0,0) to (100, 100) then the value of m=(0-100)/(0-100) = 1 thus the equation for your line is y-0=1*(x-0) => y=x

Now that we have an equation for the line in question its easy to test if a point belongs to this line. A given point (x3, y3) belongs to this line if it satisfies the line equation when you substitute x=x3 and y=y3. For example the point (10, 10) belongs to this line since 10=10 but (10,12) does not belong to this line since 12 != 10.

NOTE: For a vertical line the value of the slope (m) is infinite but for this special case you may use the equation for a vertical line directly x=c where c = x1 = x2.

Though I have to say I am not sure if this is the most efficient way of doing this. I will try and find a more efficient way when I have some more time on hand.

Hope this helps.

Answer 3

In the simplest form, just plug the coordinates into the line equation and check for equality.

Given:

Point p (X=4, Y=5)
Line l (Slope=1, YIntersect=1)

Plug in X and Y:

   Y = Slope * X + YIntersect
=> 5 = 1 * 4 + 1
=> 5 = 5

So yes, the point is on the line.

If your lines are represented in (X1,Y1),(X2,Y2) form, then you can calculate slope with:

 Slope = (y1 - y2) / (x1-x2)

And then get the Y-Intersect with this:

 YIntersect = - Slope * X1 + Y1;

Edit: I fixed the Y-Intersect (which has been X1 / Y1 ...)

You'll have to check that x1 - x2 is not 0. If it is, then checking if the point is on the line is a simple matter of checking if the Y value in your point is equal to either x1 or x2. Also, check that the X of the point is not 'x1' or 'x2'.

Answer 4

I think Mr.Patrick McDonald put the nearly correct answer and this is the correction of his answer:

public bool IsOnLine(Point endPoint1, Point endPoint2, Point checkPoint)
{
    return (((double)checkPoint.Y - endPoint1.Y)) / ((double)(checkPoint.X - endPoint1.X))
        == ((double)(endPoint2.Y - endPoint1.Y)) / ((double)(endPoint2.X - endPoint1.X));
}

and of course there are many other correct answers especially Mr.Josh but i found this is the best one.

Thankx for evryone.

Answer 5

Equation of the line is:

y = mx + c

So a point(a,b) is on this line if it satisfies this equation i.e. b = ma + c