Fitting an ellipsoid to 3D data points
I have a large set of 3D data points to which I want to fit to an ellipsoid.
My maths is pretty poor, so I\'m having trouble implementing the least squares method withou
-
I have an idea. Approximately solution, not the best but will keep points inside. In XY plane find the radius R1 that will obtain all points. Same do for the XZ plane (R2) and YZ plane (R3). Then use the maximums on each axes. A=max(R1,R2), B=max(R1,R3) and C=max(R2,R3). But, first of all find the average (center) of all points and align it to origin.
讨论(0) -
I could not find a good Java based algorithm for fitting an ellipsoid, so I ended up writing it myself. There were some good algorithms for an ellipse with 2D points, but not for an ellipsoid with 3D points. I experimented with a few different MATLAB scripts and eventually settled on Yury Petrov's Ellipsoid Fit. It fits an ellipsoid to the polynomial Ax^2 + By^2 + Cz^2 + 2Dxy + 2Exz + 2Fyz + 2Gx + 2Hy + 2Iz = 1. It doesn't use any constraints to force an ellipsoid, so you have to have a fairly large number of points to prevent a random quardic from being fit instead of the ellipsoid. Other than that, it works really well. I wrote a small Java library using Apache Commons Math that implements Yury Petrov's script in Java. The GIT repository can be found at https://github.com/BokiSoft/EllipsoidFit.
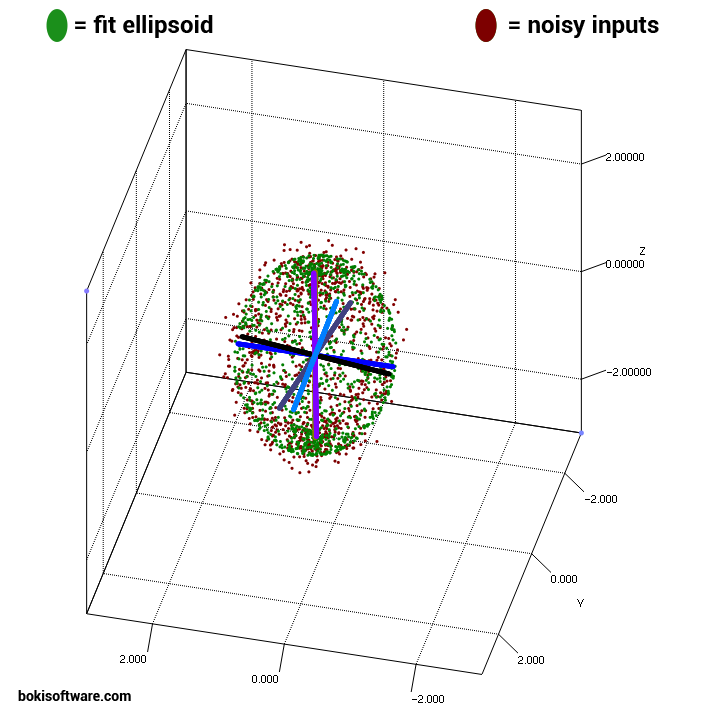 讨论(0)
讨论(0) -
here you go:
This paper describes fitting an ellipsoid to multiple dimensions AS WELL AS finding the center for the ellipois. Hope this helps,
http://www.physics.smu.edu/~scalise/SMUpreprints/SMU-HEP-10-14.pdf
(btw, I'm assuming this answer is a bit late, but I figured I would add this solution for anyone who stumbles across your question in search for the same thing :)
讨论(0) -
Here is very simple method to find foci's, based on random search. No linear algebra used. So if you are fine with non-perfect solution:
3DPoints - Array of some Amount of points vecCenter - average of 3DPoints AngleCosine - cos of angle between two vectors RandomOrder(3DPoints) vecFocus := (0, 0, 0) for i := 0 to Amount: vecRadius := 3DPoints[i] - vecCenter // Change vecRadius direction to parallel if AngleCosine(vecFocus, vecRadius) < 0 then vecRadius *= -1 vecFocus += (vecRadius - vecFocus) / AmountResult can be improved by passing array 2nd time in backward direction Foci's placed at vecCenter +/- vecFocus
讨论(0) -
Least Squares data fitting is probably a good methodology give the nature of the data you describe. The GNU Scientific Library contains linear and non-linear least squares data fitting routines. In your case, you may be able to transform your data into a linear space and use linear least-squares, but that would depend on your actual use case. Otherwise, you'll need to use non-linear methods.
讨论(0) -
I have just gone through the same process. Here is a python module which is based on work by Nima Moshtagh. Referenced in many places but also in this question about a Bounding ellipse
This module also handles plotting of the final ellipsoid. Enjoy!
https://github.com/minillinim/ellipsoid/blob/master/ellipsoid.py
讨论(0)
- 热议问题

 加载中...
加载中...