Area of a irregular shape

Question

I have set of points which lies on the image. These set of points form a irregular closed shape. I need to find the area of this shape. Does any body which is the normal algorit

Answer 1

Note: If you don't know the order of the points and cannot guarantee that your polygon is convex, it is not possible to determine the ordering of the shape, since there may be more than one possible order the points which produces a polygon. If you do know that the polygon is convex, determining the ordering of the points is easy. Merely sort the points by angle from one particular point., with the first point being the one that forms a line between itself and the initial point such that all the other points are on the same side of the line. The triangles formed by this process can also be used to calculate the area.

Answer 2

The simplest way to do this is probably to triangulate your shape and calculate the area of the triangles. Dave Eberly has a library called (Boost license) that may help with the triangulation; there is more information here. Look for TriangulateEC, for example.

Answer 3

There's a summation formula for that.

Answer 4

There is support for area calculation of polygons in Boost.Geometry (which isn't yet accepted into boost and which is very confusing to use). Otherwise you would have to determine the polygon that is defined by your points first. From the looks of it all of your points are vertices of the polygon so this is a simply a matter of ordering your point sets correctly. Another possibility is that you are looking for the convex hull of your point set (see http://en.wikipedia.org/wiki/Convex_hull_algorithms).

Answer 5

If you polygon is simple (it doesn't have any point in common except for the pairs of consecutive segments) then wikipedia comes to help you:

The formula for the area is

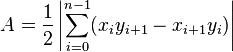
(it assumes that the last point is the same of the first one)

You can easily implement it as

float area = 0.0f;

for (int i = 0; i < numVertices - 1; ++i)
  area += point[i].x * point[i+1].y - point[i+1].x * point[i].y;

area += point[numVertices-1].x * point[0].y - point[0].x * point[numVertices-1].y;

area = abs(area) / 2.0f;

Of course vertices must be ordered according to their natural following in the polygon..

Answer 6

You might want to be more precise, possibly even providing a graphical example.

For instance, if the points you have are merely pixels, then the number of pixels equals the area. But if the points are the corners of a polygon, then the area of the polygon isn't that easily determined. You'd use polygon triangulation, and sum the areas of the triangles obtained.