What is the significance of the eigenvalues of an autocorrelation matrix in image processing?
I am working on finding corner points using the Harris corner detection algorithm. A reference paper that I am reading suggested me to examine the eigenvalues of the autocorrela
-
The eigenvalues of the autocorrelation matrix tell you what kind of feature you are looking at. The autocorrelation you are computing is based on an image patch you are looking at in the image.
Actually, what you're computing is the structure tensor. The Harris corner detector algorithm commonly refers to this matrix as the autocorrelation matrix, but it is really just a sum of squared differences. The structure tensor is a 2 x 2 matrix of sum of squared differences between two image patches within the same image.
This is how you'd compute the structure tensor in a Harris corner detector sense:

Given an image patch in your image,
IxandIyrepresent the partial derivatives of the image patch in the horizontal and vertical directions. You can use any standard convolution operation to achieve these partial derivative images, like using a Prewitt or Sobel operator.After you compute this matrix, there are three situations that you need to take a look at when looking at the autocorrelation matrix in the Harris corner detector. Note that this is a 2 x 2 matrix, and so there are two eigenvalues for this matrix.
- If both eigenvalues are close to 0, then there is no feature point of interest in the image patch you're looking at.
- If one of the eigenvalues is larger and the other is close to 0, this tells you that you are lying on an edge.
- If both of the eigenvalues are large, that means the feature point we are looking at is a corner.
However, it has been noted that calculating eigenvalues is a very computationally expensive operation, even if it's just for a 2 x 2 matrix. Therefore, Harris came up with an interest point measure instead of computing the eigenvalues to determine whether or not something is interesting. Basically, when you compute this measure, if it surpasses some set threshold, then what you have is a corner point within the centre of this patch. If it doesn't, then there is no corner point.

Mcis the "score" that is for a particular image patch to see if we have a corner point.detis the determinant of the matrix, which is justad - bc, given that your 2 x 2 matrix is in the form of[a b; c d], and thetraceis just the sum of the diagonals ora + d, given that the matrix is of the same form:[a b; c d].kappais a tunable parameter that usually ranges between 0.04 and 0.15. The threshold that you set to see whether or not we have an interesting point or an edge highly depends on your image, so you'll have to play around with this.If you want to avoid using
kappa, there is another way to estimate calculating the eigenvalues using Noble's corner measure: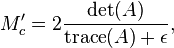
epsilonis some small constant, like0.0001. Again, to figure out whether or not you have an interesting point depends on your image. After you find all of the corner points in your image, people usually perform non-maximum suppression to suppress false positives. What this means is that you examine a neighbourhood of corner points that surround the centre of a particular corner point. If this centre corner point does not have the highest score, then this corner point is dropped. This is also performed because if you were to detect corner points using a sliding window approach, it is highly probable that you would have multiple corner points within a small vicinity of the valid one when only one or a few would suffice.
Basically, the point of looking at the eigenvalues is to check to see whether or not you are looking at an edge, a corner point, or nothing at all.
讨论(0)
- 热议问题

 加载中...
加载中...