原文地址https://blog.csdn.net/HerosOfEarth/article/details/52425952
前言：上篇博文已经介绍了ID3、C4.5生成决策树的算法。由于上文使用的测试数据以及建立的模型都比较简单，所以其泛化能力很好。但是，当训练数据量很大的时候，建立的决策树模型往往非常复杂，树的深度很大。此时虽然对训练数据拟合得很好，但是其泛化能力即预测新数据的能力并不一定很好，也就是出现了过拟合现象。这个时候我们就需要对决策树进行剪枝处理以简化模型。另外，CART算法也可用于建立回归树。本文先承接上文介绍完整分类决策树，再简单介绍回归树。
四、CART算法
CART，即分类与回归树（classification and regression tree），也是一种应用很广泛的决策树学习方法。但是CART算法比较强大，既可用作分类树，也可以用作回归树。作为分类树时，其本质与ID3、C4.5并有多大区别，只是选择特征的依据不同而已。另外，CART算法建立的决策树一般是二叉树，即特征值只有yes or no的情况（个人认为并不是绝对的，只是看实际需要）。当CART用作回归树时，以最小平方误差作为划分样本的依据。
1.分类树
(1)基尼指数
分类树采用基尼指数选择最优特征。假设有KK个类，样本点属于第kk类的概率为pkpk，则概率分布的基尼指数定义为
Gini(p)=∑k=1Kpk(1pk)=1∑k=1Kp2k
对于给定的样本集合DD，其基尼指数为Gini(D)=1∑k=1K(|Ck||D|)2
这里，CkCk是DD中属于第kk类的样本子集，KK是类的个数。 Python计算如下：
def calcGini(dataSet): ''' 计算基尼指数 :param dataSet:数据集 :return: 计算结果 ''' numEntries = len(dataSet) labelCounts = {} for featVec in dataSet: # 遍历每个实例，统计标签的频数 currentLabel = featVec[-1] if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0 labelCounts[currentLabel] += 1 Gini = 1.0 for key in labelCounts: prob = float(labelCounts[key]) / numEntries Gini -= prob * prob # 以2为底的对数 return Gini- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
那么在给定特征AA的条件下，集合DD的基尼指数定义为
Gini(D,A)=|D1|DGini(D1)+|D2||D|Gini(D2)Gini(D,A)=|D1|DGini(D1)+|D2||D|Gini(D2)
基尼指数Gini(D)Gini(D)表示集合D的不确定性，基尼指数Gini(D,A)Gini(D,A)表示经A=aA=a分割后集合DD的不确定性。基尼指数值越大，样本集合的不确定性也就越大，这一点与熵相似。 Python计算如下：
def calcGiniWithFeat(dataSet, feature, value): ''' 计算给定特征下的基尼指数 :param dataSet:数据集 :param feature:特征维度 :param value:该特征变量所取的值 :return: 计算结果 ''' D0 = []; D1 = [] # 根据特征划分数据 for featVec in dataSet: if featVec[feature] == value: D0.append(featVec) else: D1.append(featVec) Gini = len(D0) / len(dataSet) * calcGini(D0) + len(D1) / len(dataSet) * calcGini(D1) return Gini- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
(2)CART分类树的算法步骤如下： 
Python实现如下：
def chooseBestSplit(dataSet): numFeatures = len(dataSet[0])-1 bestGini = inf; bestFeat = 0; bestValue = 0; newGini = 0 for i in range(numFeatures): featList = [example[i] for example in dataSet] uniqueVals = set(featList) for splitVal in uniqueVals: newGini = calcGiniWithFeat(dataSet, i, splitVal) if newGini < bestGini: bestFeat = i bestGini = newGini return bestFeat # for featVec in dataSet: # for splitVal in set(dataSet[:,featIndex].tolist()): # newGini = calcGiniWithFeat(dataSet, featIndex, splitVal) # if newGini < bestGini: # bestFeat = featIndex # bestValue = splitVal # bestGini = newGini def majorityCnt(classList): ''' 采用多数表决的方法决定叶结点的分类 :param: 所有的类标签列表 :return: 出现次数最多的类 ''' classCount={} for vote in classList: # 统计所有类标签的频数 if vote not in classCount.keys(): classCount[vote] = 0 classCount[vote] += 1 sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) # 排序 return sortedClassCount[0][0] def createTree(dataSet,labels): ''' 创建决策树 :param: dataSet:训练数据集 :return: labels:所有的类标签 ''' classList = [example[-1] for example in dataSet] if classList.count(classList[0]) == len(classList): return classList[0] # 第一个递归结束条件：所有的类标签完全相同 if len(dataSet[0]) == 1: return majorityCnt(classList) # 第二个递归结束条件：用完了所有特征 bestFeat = chooseBestSplit(dataSet) # 最优划分特征 bestFeatLabel = labels[bestFeat] myTree = {bestFeatLabel:{}} # 使用字典类型储存树的信息 del(labels[bestFeat]) featValues = [example[bestFeat] for example in dataSet] uniqueVals = set(featValues) for value in uniqueVals: subLabels = labels[:] # 复制所有类标签，保证每次递归调用时不改变原始列表的内容 myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels) return myTree - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
代码结构跟上篇博文是基本一样的，不同的只有选择特征的方式。所以就不在此浪费口舌了。我们导入数据测试一下：
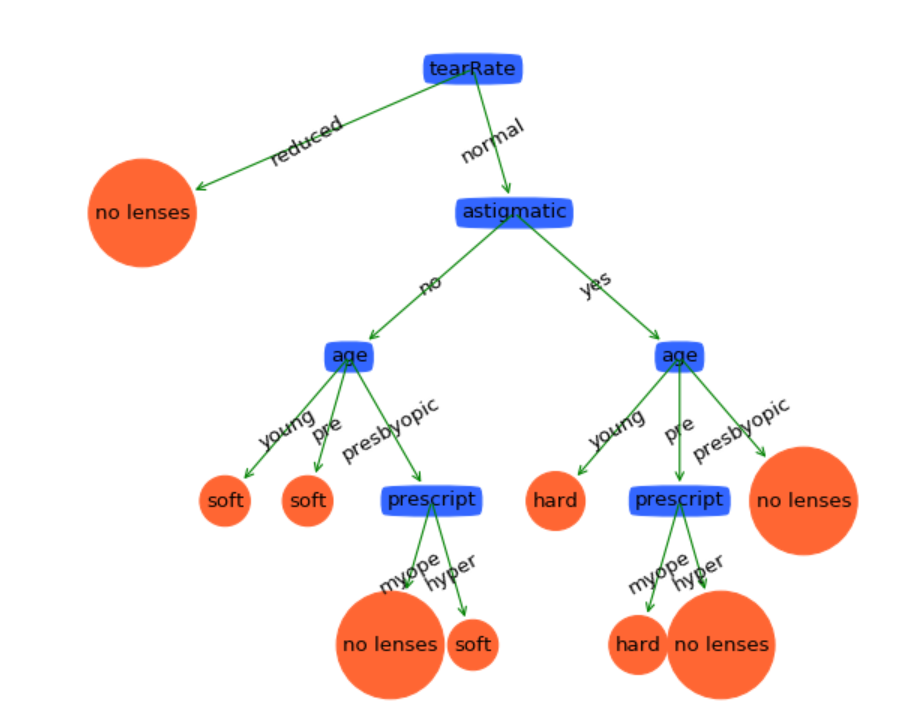
if __name__ == "__main__": dataSet,labels = createDataSet() subLabels = labels[:] myTree = createTree(dataSet, labels) print(myTree) treePlotter.createPlot(myTree)- 1
- 2
- 3
- 4
- 5
- 6
可见这棵决策树是非常复杂的。我们可以测试一下它的泛化能力。计算预测误差的代码如下：
# 计算预测误差 def calcTestErr(myTree,testData,labels): errorCount = 0.0 for i in range(len(testData)): if classify(myTree,labels,testData[i]) != testData[i][-1]: errorCount += 1 return float(errorCount)- 1
- 2
- 3
- 4
- 5
- 6
- 7
导入测试数据：
testData,testLabels = loadTestData() testErr = calcTestErr(myTree, testData, subLabels)- 1
- 2
测试数据集中有6组样本。由结果可知，有一组样本预测不正确，那么预测误差率为16.7%左右。实际上这个模型并不是很好用的，尤其是在数据量更大的预测集中。此时我们需要简化这棵决策树，防止过拟合现象。
2.剪枝（pruning）
在决策树学习中将已生成的树进行简化的过程称为剪枝。决策树的剪枝往往通过极小化决策树的损失函数或代价函数来实现。实际上剪枝的过程就是一个动态规划的过程：从叶结点开始，自底向上地对内部结点计算预测误差以及剪枝后的预测误差，如果两者的预测误差是相等或者剪枝后预测误差更小，当然是剪掉的好。但是如果剪枝后的预测误差更大，那就不要剪了。剪枝后，原内部结点会变成新的叶结点，其决策类别由多数表决法决定。不断重复这个过程往上剪枝，直到预测误差最小为止。剪枝的实现代码如下：
# 计算预测误差 def calcTestErr(myTree,testData,labels): errorCount = 0.0 for i in range(len(testData)): if classify(myTree,labels,testData[i]) != testData[i][-1]: errorCount += 1 return float(errorCount) # 计算剪枝后的预测误差 def testMajor(major,testData): errorCount = 0.0 for i in range(len(testData)): if major != testData[i][-1]: errorCount += 1 return float(errorCount) def pruningTree(inputTree,dataSet,testData,labels): firstStr = list(inputTree.keys())[0] secondDict = inputTree[firstStr] # 获取子树 classList = [example[-1] for example in dataSet] featKey = copy.deepcopy(firstStr) labelIndex = labels.index(featKey) subLabels = copy.deepcopy(labels) del(labels[labelIndex]) for key in list(secondDict.keys()): if isTree(secondDict[key]): # 深度优先搜索,递归剪枝 subDataSet = splitDataSet(dataSet,labelIndex,key) subTestSet = splitDataSet(testData,labelIndex,key) if len(subDataSet) > 0 and len(subTestSet) > 0: inputTree[firstStr][key] = pruningTree(secondDict[key],subDataSet,subTestSet,copy.deepcopy(labels)) if calcTestErr(inputTree,testData,subLabels) < testMajor(majorityCnt(classList),testData): # 剪枝后的误差反而变大，不作处理，直接返回 return inputTree else: # 剪枝，原父结点变成子结点，其类别由多数表决法决定 return majorityCnt(classList)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
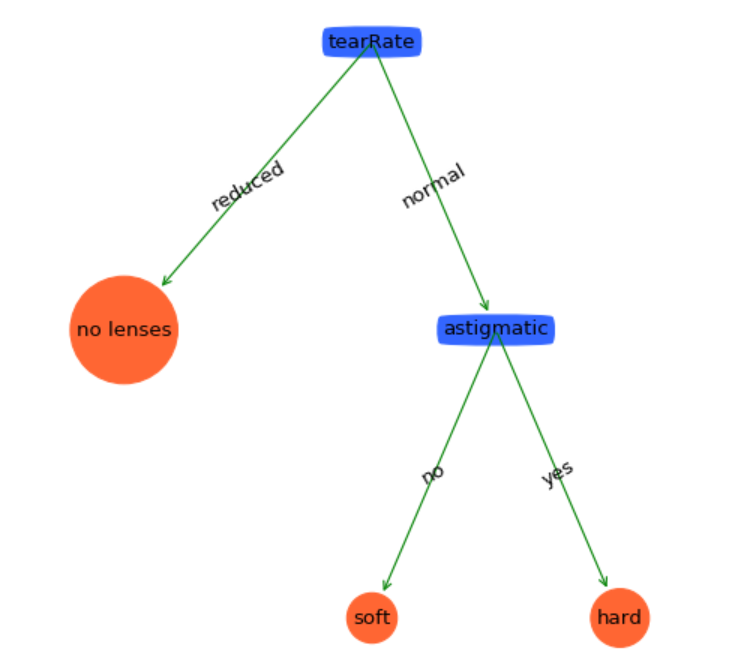
剪枝后的决策树如下： 
真的是简单得太多了。看看它的泛化能力： 
哈哈，预测能力达到100%哦！（这只是一个很小型的测试数据集而已，实际上很少有达到100%泛化能力的模型的。）从这里可以看出剪枝效果非常好！
3.回归树
回归树的生成实际上也是贪心算法。与分类树不同的是回归树处理的数据连续分布的。废话不多说了，直接贴算法： 
CART回归树算法划分样本的依据是最小平方误差。Python实现如下：
# 生成叶结点 def regLeaf(dataSet): return mean(dataSet[:,-1]) # 计算平方误差 def regErr(dataSet): return var(dataSet[:,-1]) * shape(dataSet)[0] def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)): tolS = ops[0]; tolN = ops[1] if len(set(dataSet[:,-1].T.tolist())) == 1: # 停止条件：样本属于同一个类 return None, leafType(dataSet) m,n = shape(dataSet) S = errType(dataSet) bestS = inf; bestIndex = 0; bestValue = 0 for featIndex in range(n-1): for splitVal in set(dataSet[:,featIndex].tolist()):# 固定特征，并为每个特征选择最优二分特征值 R0, R1 = binSplitDataSet(dataSet, featIndex, splitVal) if (shape(R0)[0] < tolN) or (shape(R1)[0] < tolN): continue newS = errType(R0) + errType(R1) if newS < bestS: bestIndex = featIndex bestValue = splitVal bestS = newS # 如果误差下降值小于一个阈值，则不要划分 if (S - bestS) < tolS: return None, leafType(dataSet) #exit cond 2 R0, R1 = binSplitDataSet(dataSet, bestIndex, bestValue) if (shape(R0)[0] < tolN) or (shape(R1)[0] < tolN): # 停止条件:样本数小于一个阈值 return None, leafType(dataSet) return bestIndex,bestValue- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
构建回归树如下：
def createTree(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):#assume dataSet is NumPy Mat so we can array filtering feat, val = chooseBestSplit(dataSet, leafType, errType, ops)# 选择最优二分方式 if feat == None: return val retTree = {} retTree['spInd'] = feat retTree['spVal'] = val leftSet, rightSet = binSplitDataSet(dataSet, feat, val) retTree['left'] = createTree(leftSet, leafType, errType, ops) retTree['right'] = createTree(rightSet, leafType, errType, ops) return retTree- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
回归树同样有一个剪枝过程：
def isTree(obj): return (type(obj).__name__=='dict') def getMean(tree): if isTree(tree['right']): tree['right'] = getMean(tree['right']) if isTree(tree['left']): tree['left'] = getMean(tree['left']) return (tree['left']+tree['right'])/2.0 def prune(tree, testData): if shape(testData)[0] == 0: return getMean(tree) # 如果没有测试数据则对树进行塌陷处理 if (isTree(tree['right']) or isTree(tree['left'])): lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal']) # 深度优先搜索 if isTree(tree['left']): tree['left'] = prune(tree['left'], lSet) if isTree(tree['right']): tree['right'] = prune(tree['right'], rSet) # 到达叶结点 if not isTree(tree['left']) and not isTree(tree['right']): lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal']) # 未剪枝的误差 errorNoMerge = sum(power(lSet[:,-1] - tree['left'],2)) +\ sum(power(rSet[:,-1] - tree['right'],2)) treeMean = (tree['left']+tree['right'])/2.0 # 剪枝后的误差 errorMerge = sum(power(testData[:,-1] - treeMean,2)) if errorMerge < errorNoMerge: print("merging") return treeMean else: return tree else: return tree- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
相比线性回归，回归树可以对非线性数据建立模型。这个算法可以使用任意一个测试线性回归的数据集来测试，这里就不再演示了。
五、总结
总体来讲，决策树模型是一个比较容易理解模型。它建立起来的模型直观、形象，也比较贴近人们的思维习惯。决策树更多地用于分类问题而不是回归问题。通常，在使用更复杂的算法之前，一般先建议使用决策树，并将它的准确率作为性能基准。另外，决策树还可以帮助我们提取重要特征。作为机器学习十大算法之一，决策树有着它相当重要的地位，基本上市面上能见到的机器学习书籍必定会讲这个算法。然而，决策树的研究并不止于此。关于决策树更深的模型有软决策树、决策森林、随机森林等。
分类树测试数据（包含训练集和测试集）：http://download.csdn.net/detail/herosofearth/9621052