相控阵天线中,直线阵列作为重要的一种,有着极为广泛的应用。切比雪夫低副瓣阵列设计是一种典型的设计方法。
切比雪夫方法主要是实现低副瓣、窄波束:
其产生的核心如下:
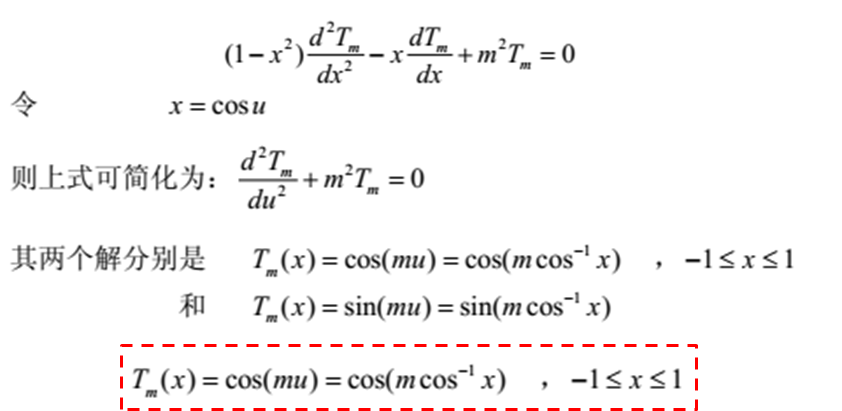
我的理解:因为能量守恒,所有副瓣都一样的时候,能量会更多的集中在副瓣中,
主瓣最大增益也不会改变,这样就可以使主瓣窄,副瓣电平降低。G=4πS/λ2

结合切比雪夫函数,可以得到:
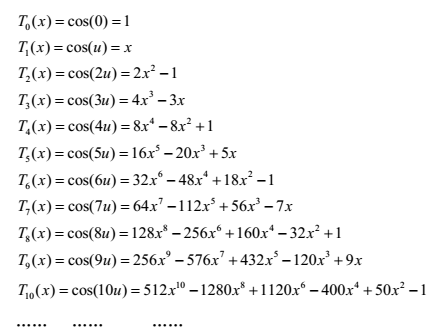


当具体应用时,解决方案如下:

话不多说,其Matlab中的程序如下:
1 % 2019-11 2 % 切比雪夫低副瓣阵列馈电设计_1.0 (端射阵) 3 4 close all; 5 clear 6 % digits(3); 7 8 % 参数设置 9 lamda = 1; % 波长 10 d = lamda * 0.6; % d为阵元间距 11 theta0 = (100/180)*pi; % 扫描角度 12 theta = 0: 0.01 : pi; % Θ为方向角 13 u = pi*d*(cos(theta)-cos(theta0))/lamda; 14 %T = Chebyshev; % T为切比雪夫恒等式系数矩阵 15 N = 10; % N为直线阵的阵元数量,M为一侧的单元数(对称) 16 R0dB = 26; % R0dB为副瓣电平 17 18 if (mod(N,2)==0) 19 M = N / 2; 20 parity = 0; % parity为奇偶性,0为偶数 21 else 22 M = (N+1)/2; 23 parity = 1; 24 end 25 26 % 导入切比雪夫多项式 27 syms x; 28 T = [ 29 1; 30 x; 31 2*x^2-1; 32 4*x^3-3*x; 33 8*x^4-8*x^2+1; 34 16*x^5-20*x^3+5*x; 35 32*x^6-48*x^4+18*x^2-1; 36 64*x^7-112*x^5+56*x^3-7*x; 37 128*x^8-256*x^6+160*x^4-32*x^2+1; 38 256*x^9-576*x^7+432*x^5-120*x^3+9*x; 39 512*x^10-1280*x^8+1120*x^6-400*x^4+50*x^2-1 40 ]; 41 42 43 % 换算副瓣电平R0 44 R0 = 10 ^ (R0dB / 20); 45 46 % 计算x0 47 x0 = ((R0 + sqrt(R0^2 -1))^(1/(N-1)) + (R0 - sqrt(R0^2 -1))^(1/(N-1))) * 1/2; 48 49 % 定义馈电幅度矩阵I 50 I = sym('I', [1 M]); 51 52 % 计算展开的方向图表达式 53 S = T(2) * I(1); 54 55 for k = 2 : M 56 S = S + T(2*k) * I(k); 57 end 58 59 %collect(S,x) 60 %vpa(S) 61 62 S_po = coeffs(S,x); % 含电流的方向图多项式系数 63 T_po = sym2poly(T(N)); % 标准的方向图多项式系数(反向了) 64 T_PO = zeros(1,M); 65 for k = 1 : M 66 T_PO(k) = T_po(2*k-1); 67 S_po(k) = S_po(k)/x0^(2*k-1); 68 end 69 % T_PO 70 % vpa(S_po) 71 72 % 系数比较求出电流大小 73 eq = sym('eq',[M 1]); % 系数比较恒等式 74 for k = 1 : M 75 eq(k) = S_po(k) == T_PO(M+1-k); 76 end 77 78 vpa(eq) 79 I_st = solve(eq); 80 I_ce = struct2cell(I_st); 81 i = zeros(M,1); % 最终的电流矩阵 82 for k = 1 : M 83 i(k) = I_ce{k,1}; 84 i(k) = i(k); 85 end 86 for k = 2 : M 87 i(k) = i(k)/i(1); % 电流归一化 88 end 89 i(1) = 1; i 90 i=[1;0.89;0.706;0.485;0.357]; % 用来检验的数据 91 92 % 计算最终的阵因子 93 S_all = zeros(1,length(theta)); 94 for k = 1 : M 95 S_all = S_all + i(k)*cos((2*k-1)*u); 96 end 97 SS = S_all; 98 99 % 画图 ―― 直角坐标系 100 S_max = max(S_all); % 归一化处理 101 S_all = 20*log10(S_all/S_max); % 取分贝值 102 figure('NumberTitle', 'off', 'Name', 'S Parameter (dB) - Cartesian'); 103 theta_ = theta * 180 / pi; 104 plot(theta_,S_all,'k','LineWidth',1.5); 105 grid off 106 xlabel('\theta (°)','FontSize',13); 107 ylabel('|S| dB','FontSize',12); 108 axis([0 182 -50 2]); 109 box on 110 111 % 画图 ―― 极坐标系 112 figure('NumberTitle', 'off', 'Name', 'S Parameter (dB) - Polar'); 113 S_pol = SS / max(SS); 114 polarplot(theta,S_all,'k','LineWidth',1.5); 115 thetalim([0 180]); 116 rmin = min(S_all); 117 rmax = max(S_all); 118 rlim([-50 rmin]); 上述测试的N=10的10个阵列,侧射阵(θ=0),副瓣电平SLL=26dB,结果如下:

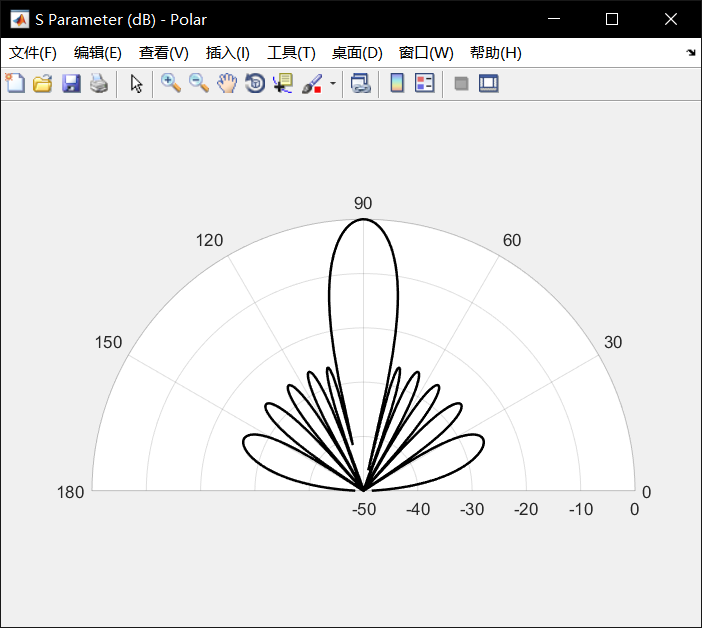
更改一下theta0的值,改为120读,即偏离法相30度:
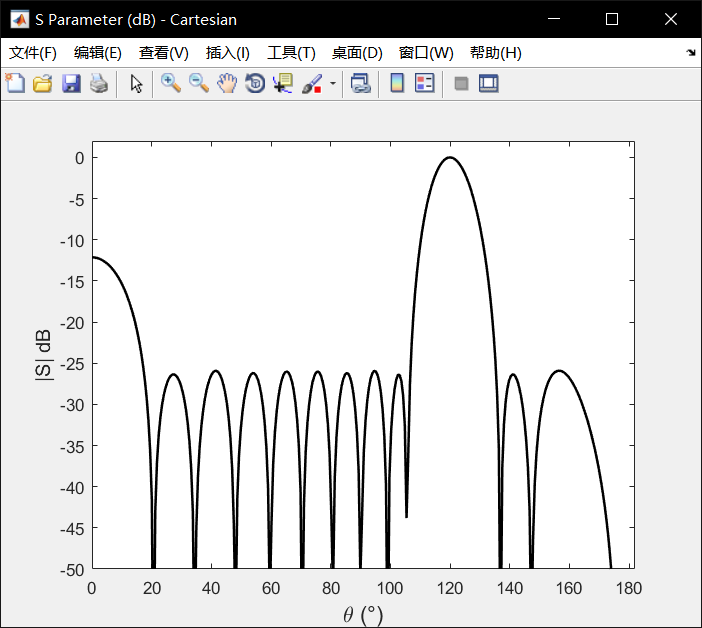

来源:博客园
作者:olivermahout
链接:https://www.cnblogs.com/olivermahout/p/11784999.html