来源:大数据算法 王宏志
一、概述
大数据定义:在给定的资源约束下,以大数据为输入,在给定时间约束内可以生成满足给定约束结果的算法。
大数据特点:4V
大数据算法可以不是:
- 精确算法
- 内存算法
- 串行算法
- 仅在电子计算机上运行的算法
大数据算法不仅是:
- 云计算
- MapReduce
- 大数据分析和挖掘的算法
难度:
- 访问全部数据时间过长
读取部分数据 亚线性算法
- 数据难以放入内存
将数据存储到磁盘上 外存算法
仅基于少量数据进行计算 空间亚线性算法
- 单个计算机难以保存全部数据
并行处理 并行算法
- 计算机能力不足或知识不足
人来帮忙 众包算法
大数据上问题求解计算问题的过程
大数据的算法设计技术
- 精确算法设计方法
- 并行计算
- 近似计算
- 随机算法
- 在线算法/数据流算法
- 外存算法
- 面向新型体系结构的算法
- 现代优化算法
大数据算法分析
- 时间空间复杂性
- IO复杂性
- 结果质量(近似比、competitive ratio)
- 通讯复杂性
二、亚线性算法概述
1.定义
时间/空间/IO/通讯/能量等消耗是o(输入规模)
亚线性时间算法
- 性质检测算法
- 亚线性时间近似算法
亚线性空间算法
- 数据流算法
2.空间亚线性算法-水库抽样
输入:一组数据,其大小未知
输出:这组数据的k个均匀抽样
要求:
- 仅扫描数据一次
- 空间复杂性为O(k) 和抽样大小有关,和整个数据无关
- 扫描到数据的前n个数字时(n>k),保存当前已扫描数据的k个均匀抽样
算法:
- 申请一个长度为k的数组A保存抽样
- 保存首先接收到的k个元素
- 当接收到第i个新元素t时,以k/i的概率随机替换A中的元素(即生成[1, i]间随机数j,若k<=j,则以t替换A[j]

3.时间亚线性计算算法-平面图直径
输入:m个顶点的平面图,任意两点之间的距离存储在矩阵D中,即点i到点j的距离为Dij
- 输入大小是n=m的平方
- 最大的Dij是图的直径
- 点之间的距离对称且满足三角不等式
输出:该图的直径和距离最大的Dij
要求:运行时间为o(n)
算法:
动机:无法在要求的时间内得到精确算法,寻找近似算法
近似算法
- 任意选择k<=m
- 选择使得Dkl最大的l
- 输出Dkl和(k, l)
近似比
Dij <= Dik+Dkj <= Dkl+Dk l<= 2Dkl 因而近似比为2
近似时间
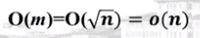
4.近似算法
什么是近似算法
- 近似算法主要用来解决优化问题
- 能够给出一个优化问题的近似优化解的算法
近似算法解的近似度
- 问题的每一个可能的解都具有一个代价
- 问题的优化解可能具有最大或最小代价
- 我们希望寻找问题的一个误差最小的近似优化解
我们需要分析近似解代价与优化解代价的差距
- Ratio Bound
- 相对误差
- (1-ε)-近似
5.时间亚线性判定算法-全0数组判定
输入:包含n个元素的0,1数组A
输出:A中的元素是否全是0
要求:运行时间为o(n)
判定问题的近似:
- 无法在要求的时间内得到精确解,寻找近似解
判定问题如何近似
- 输入满足某种性质或者远非满足此性质

- ε-远离
对于输入x,如果x到L中的任意字符串的汉明距离至少为ε|x|,则x是ε-远离L的
全0数组判定问题的近似
- 是否A=00...0或者其包含1的个数大于 εn?
算法描述:
- 在A中随机独立抽取s= 2/ε个位置上的元素
- 检查抽样,若不包含1,则输出“是”,若包含1,则输出“否”
判定精确性分析
- 如果A是全0数组,始终输出“是”
- 如果A是 ε-远离的,

运行时间:O(s)
证据引理:
- 如果一次测试以大于等于p的概率获得一个证据,那么s=2/p轮测试得到证据的概率大于等于2/3
判定算法的定义

三、亚线性算法案例

来源:博客园
作者:AI数据
链接:https://www.cnblogs.com/aidata/p/11555808.html


